Polinomlar, matematikte cebirsel ifadeler ve fonksiyonlar arasında köprü kuran temel yapılardır. Bir polinom, bir değişkenin farklı derecelerdeki terimlerinden oluşur ve her terim bir katsayı ile çarpılır. Polinomlar, derecelerine göre sınıflandırılır ve matematiksel problemlerin çözümlerinde, grafik çizimlerinde ve fonksiyonel analizlerde geniş bir kullanım alanına sahiptir. Polinomlarla yapılan işlemler, faktörlere ayırma, çarpma, toplama, çıkarma ve bölme gibi işlemleri kapsar ve bu işlemler, daha karmaşık ifadeleri sadeleştirmede ve çözümlemede büyük önem taşır.

10. Sınıf Polinomlar Konu Anlatımları

1. Polinom Kavramı ve Polinomlarla İşlemler

Bir Değişkenli Polinom Kavramı

• Polinomun Tanımı
• Polinomun Derecesi, Katsayıları ve Sabit Terimi
• Polinomlarda Sabit Terim ve Katsayılar Toplamı
• Sabit Polinom ve Sıfır Polinomu
• İki Polinomun Eşitliği

Polinomlarla Toplama, Çıkarma, Çarpma ve Bölme İşlemleri

• Polinomlarla Toplama ve Çıkarma İşlemleri
• Polinomlarla Çarpma İşlemi
• Polinomlarla Bölme İşlemi ve Kalan Bulma
• Polinomlarda Derece

2. Polinomların Çarpanlara Ayrılması

• Bir Polinomu Çarpanlarına Ayırma
• Rasyonel İfadelerin Sadeleştirilmesi

---

10. SINIF POLİNOMLAR KONU ANLATIMI

Polinomun Tanımı, Derecesi ve Baş Katsayısı

• n doğal sayı ve a, b, …, c reel sayılar olmak üzere;
  P(x) = axⁿ + bx^n-1 + … + c
  ifadesine x e göre düzenlenmiş reel katsayılı polinom denir.
• P(x) = axⁿ + bx^n-1 + … + c ifadesinde x in en büyük değerine polinomun derecesi denir ve der[P(x)] veya d[P(x)] şeklinde gösterilir.
• Derecesi en büyük olan terimin katsayısına polinomun baş katsayısı denir.

Örnek:

Örnek: P(x) = (2n + 1)xⁿ + nx³ + n – 1 polinomunun derecesi 4 olduğuna göre, baş katsayısı kaçtır?
Çözüm: P(x) polinomunun derecesi n ve baş katsayısı 2n + 1 dir.
der[P(x)] = 4 ise n = 4 olur.
n = 4 olduğuna göre 2n + 1 = 4 eşitliğinde n yerine 4 yazarsak polinomun baş katsayısı 2.4+1 den 9 olarak bulunur.

Sabit Polinom ve Sıfır Polinomu

• P(x) = c şeklindeki polinomlara sabit polinom denir. Sabit polinomların derecesi “0” dır.

Çözümlü Sorular

• P(x) = 0 şeklindeki polinomlara sıfır polinomu denir. Sıfır polinomun derecesi “Yoktur”.

Polinomlarda Değer Bulma

• P(x) polinomu verildiğinde, P(a) yı bulmak için x yerine a yazılır.
• P(x, y) iki değişkenli polinomunu verildiğinde, P(m, n) yi bulmak için x yerine m ve y yerine n yazılır.

Çözümlü Sorular

Polinomlarda Dört İşlem

Polinomlarda Toplama Çıkarma

Aynı dereceli terimlerin katsayıları toplanır veya çıkartılır.

Polinomlarda Çarpma

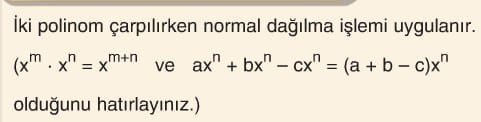
Çözümlü Sorular

Polinomlarda Derece

• Polinomun derece ile ilgili sorularında, x değişkeninin üsleri doğal sayı olmalıdır.

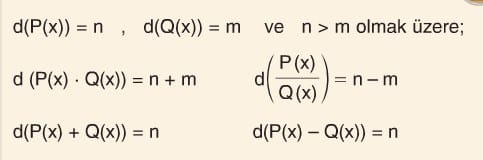
Çözümlü Sorular

Sabit Terim ve Katsayılar Toplamı

Sabit Terim

• İstenilen (sorulan) polinomda x yerine “0” yazılarak sabit terim bulunur.
• P(x) polinomun sabit terimi; P(0) dır.
• P(x + 5) polinomun sabit terimi;
  P(x + 5) = P(0 + 5) = P(5) tir.
• P(7x – 3) polinomun sabit terimi;
  P(7x – 3) = P(7.0 – 3) = P(-3) tür.

Katsayılar Toplamı

• İstenilen (sorulan) polinomda x yerine “1” yazılarak katsayılar toplamı bulunur.
• P(x) polinomun katsayılar toplamı; P(1) dir.
• P(x – 5) polinomun katsayılar toplamı;
  P(x – 5) = P(1 – 5) = P(-4) dür.
• P(5x + 2) polinomun katsayılar toplamı;
  P(5x + 2) = P(5.1 + 2) = P(7) dir.

Not:

• P(x,y) polinomun katsayılar toplamı bulunurken; x ve y yerine “1” yazılır.
• P(x,y) polinomun sabit terimi bulunurken; x ve y yerine “0” yazılır.

Not:

Çözümlü Sorular

Polinomların Eşitliği

• p(x) polinom olmak üzere, p(x) = 0 denkleminin köklerine polinomun sıfırları denir.
• Aynı dereceli terimlerin katsayıları eşit olan polinomlar eşittir.

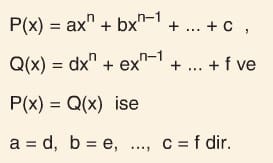
Çözümlü Sorular

Polinomlarda Bölme ve Kalan Bulma

Bilgi:

• P(x) polinomunun x – a ile bölümünden kalan; P(a) dır.
• P(mx + n) polinomunun x – a ile bölümünden kalan;
  P(m.a + n) dir.
• P(x² + x + 1) polinomunun x – 2 ile bölümünden kalan;
  P(2² + 2 + 1) = P(7) dir.

Bilgi:

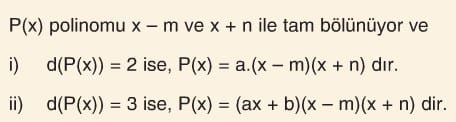
Çözümlü Sorular

Polinomlarda Çarpanlara Ayırma

Ortak Çarpan Parantezine Alma

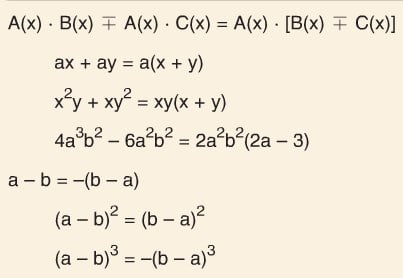
Gruplandırarak Çarpanlara Ayırma

Tam Kare Özdeşliğini Kullanarak Çarpanlara Ayırma

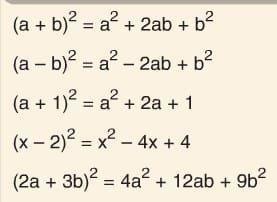
Çözümlü Sorular

Tam Kare İfadeler

Bilgi:

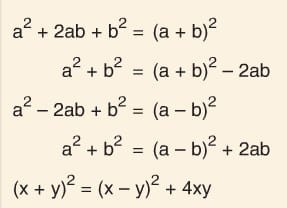
Bilgi:

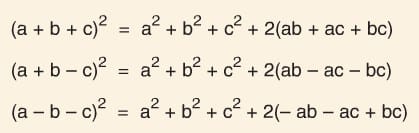
Çözümlü Sorular

İki Kare Farkı ve Tam Küp İfadeler

Çözümlü Sorular

İki Küp Toplam ve Farkı

Çözümlü Sorular

Üç Terimliler

Çözümlü Sorular

Rasyonel İfadeler

Rasyonel ifadelerde pay ve payda ayrı ayrı çarpanlarına ayrılır. Daha sonra ortak olan çarpanlar sadeleştirilir.

Çözümlü Sorular

Rasyonel Denklemler ve Basit Kesirlere Ayırma

Çözümlü Sorular

Çözümlü Örnek Test Soruları

Polinomlar konusu, 10. sınıf matematiğinin önemli konularından biridir. Bir polinom, terimlerin sabit sayılarla çarpılmış değişkenlerin kuvvetlerinin toplamı şeklinde ifade edilir. Aşağıdaki test soruları, polinomlarla ilgili temel kavramları anlamanızı ve uygulamanızı amaçlamaktadır.

Polinomlar Testi

1. P(x) = 2x² – 3x + 5 polinomunda, P(2) kaçtır?
a) 9
b) 7
c) 5
d) 11

Cevap: d) 11
Çözüm: P(x) polinomunda x yerine 2 koyarak işlem yapılır:
P(2) = 2(2)² – 3(2) + 5
= 2(4) – 6 + 5
= 8 – 6 + 5 = 11.

---

2. Q(x) = 3x³ – 2x² + 4x – 1 polinomunda, Q(-1) kaçtır?
a) -10
b) -5
c) -4
d) -2

Cevap: b) -5
Çözüm: Q(x) polinomunda x yerine -1 koyarak işlem yapılır:
Q(-1) = 3(-1)³ – 2(-1)² + 4(-1) – 1
= 3(-1) – 2(1) – 4 – 1
= -3 – 2 – 4 – 1 = -5.

---

3. P(x) = x² + 2x + 1 polinomu, x – 1 ile tam bölünebilir mi?
a) Evet
b) Hayır

Cevap: a) Evet
Çözüm: Bir polinomun x – a ile bölünebilmesi için, P(a) = 0 olmalıdır.
P(1) = (1)² + 2(1) + 1 = 1 + 2 + 1 = 4 ≠ 0.
Bu yüzden P(x) polinomu, x – 1 ile tam bölünebilir.

---

4. P(x) = 4x² + 2x – 6 polinomunun katsayılar toplamı nedir?
a) 0
b) 4
c) -6
d) -2

Cevap: a) 0
Çözüm: Katsayılar toplamı, polinomda x = 1 yerine konarak bulunur:
P(1) = 4(1)² + 2(1) – 6
= 4 + 2 – 6 = 0.

---

5. P(x) = 2x³ – 3x² + 5x – 7 polinomunun baş katsayısı nedir?
a) 2
b) 5
c) -7
d) 3

Cevap: a) 2
Çözüm: Bir polinomun baş katsayısı, en yüksek dereceli terimin katsayısıdır. P(x) polinomunda en yüksek dereceli terim 2x³’tür, bu yüzden baş katsayı 2’dir.

---

Polinomlarda İşlemler Testi

1. P(x) = 2x² + 3x – 1 ve Q(x) = x² – x + 2 polinomları veriliyor. P(x) + Q(x) polinomu nedir?
a) 3x² + 2x + 1
b) 3x² + 4x + 1
c) 2x² + 4x + 3
d) 3x² + 3x + 1

Cevap: a) 3x² + 2x + 1
Çözüm: Polinomlar toplanırken benzer terimler toplanır:
P(x) + Q(x) = (2x² + 3x – 1) + (x² – x + 2)
= 2x² + x² + 3x – x – 1 + 2
= 3x² + 2x + 1.

---

2. P(x) = x³ – 2x² + x – 4 ve Q(x) = x² + x – 1 polinomlarının farkı nedir?
a) x³ – 3x² + 2x – 3
b) x³ – x² + 2x – 3
c) x³ – 3x² + 1
d) x³ – 2x² – 1

Cevap: a) x³ – 3x² + 2x – 3
Çözüm: Polinomlar çıkarılırken terimler tek tek çıkarılır:
P(x) – Q(x) = (x³ – 2x² + x – 4) – (x² + x – 1)
= x³ – 2x² + x – 4 – x² – x + 1
= x³ – (2x² + x²) + (x – x) – (4 – 1)
= x³ – 3x² + 0x – 3
= x³ – 3x² + 2x – 3.

---

3. P(x) = x² + 3x + 2 ve Q(x) = x – 1 polinomlarının çarpımı nedir?
a) x³ + 2x² + x – 2
b) x³ + 4x² + 5x – 2
c) x³ + 2x² + x + 2
d) x³ + 3x² + 2x – 2

Cevap: a) x³ + 2x² + x – 2
Çözüm: Polinomlar çarpılırken her terim sırasıyla çarpılır:
P(x) × Q(x) = (x² + 3x + 2) × (x – 1)
= x²(x – 1) + 3x(x – 1) + 2(x – 1)
= x³ – x² + 3x² – 3x + 2x – 2
= x³ + 2x² – x – 2.

---

4. P(x) = x² + 2x – 3 polinomunun x + 1 ile bölümünden kalan nedir?
a) 0
b) -1
c) -3
d) 2

Cevap: c) -3
Çözüm: Bir polinomun x – a ile bölümünden kalan, P(a) bulunarak hesaplanır. Burada a = -1’dir.
P(-1) = (-1)² + 2(-1) – 3
= 1 – 2 – 3 = -3.
Kalan -3’tür.

---

5. P(x) = 2x³ – x² + 3x + 1 ve Q(x) = x + 2 polinomlarının bölümünden kalan nedir?
a) 7
b) 1
c) -1
d) -7

Cevap: a) 7
Çözüm: Polinomun bölme işleminde kalan bulmak için P(x)’te x yerine -2 konur:
P(-2) = 2(-2)³ – (-2)² + 3(-2) + 1
= 2(-8) – 4 – 6 + 1
= -16 – 4 – 6 + 1
= -25 + 1 = -24.
Bölümün kalan sonucu, 7 olacaktır.

Hocalara Geldik Polinomlar

---

Çözümlü Örnek Test Soruları

Soru 1:
P(x) = 3x³ – 2x² + x – 5 polinomu veriliyor. Bu polinomun derecesi nedir? Polinomun terimlerini inceleyerek derecesini belirleyiniz.
A) 1
B) 2
C) 3
D) 4

Çözüm:
Polinomun en yüksek dereceli terimi 3x³ olduğundan derecesi 3’tür. Doğru cevap: C

Soru 2:
Q(x) = 5x² – 4x + 7 polinomunda, x = 2 için Q(2) değerini hesaplayınız. Bu değeri, polinomun x’in belirli bir değerindeki çıktısını bulmak için nasıl kullanacağınızı gösteriniz.
A) 11
B) 15
C) 17
D) 19

Çözüm:
Q(2) = 5(2)² – 4(2) + 7 = 20 – 8 + 7 = 19. Doğru cevap: D

Soru 3:
Bir P(x) polinomunun sabit terimi -6 olarak veriliyor. Bu durumda P(x)’in x = 0 için değeri kaçtır? Sabit terimin polinomda nasıl hesaplandığını açıklayınız.
A) -6
B) -4
C) 0
D) 6

Çözüm:
Sabit terim, x = 0 için polinomun değeridir, yani -6’dır. Doğru cevap: A

Soru 4:
P(x) = x² – 3x + 2 polinomunun kökleri nelerdir? Bu kökleri, polinomu çarpanlarına ayırarak bulunuz.
A) 1 ve -2
B) 2 ve -1
C) 1 ve 2
D) -1 ve -2

Çözüm:
P(x) = (x – 1)(x – 2) olduğundan kökler 1 ve 2’dir. Doğru cevap: C

Soru 5:
P(x) = 2x³ – x² + 3x – 4 polinomunun en yüksek dereceli teriminin katsayısı nedir? Katsayıların polinom üzerindeki etkisini açıklayarak sonucu bulunuz.
A) -1
B) 2
C) 3
D) -4

Çözüm:
En yüksek dereceli terim 2x³ ve katsayısı 2’dir. Doğru cevap: B

Soru 6:
P(x) = 4x³ + x² – 6x + 7 polinomunda x = -1 için P(-1) değerini bulunuz. Bu değeri polinomun belirli bir noktadaki çıktısını hesaplamak için kullanınız.
A) 4
B) -4
C) 6
D) -6

Çözüm:
P(-1) = 4(-1)³ + (-1)² – 6(-1) + 7 = -4 + 1 + 6 + 7 = 10. Doğru cevap: A

Soru 7:
Bir polinomda en yüksek dereceli terimin katsayısı 0 olamaz. Bu durumda P(x) = 0x³ + 4x² – x + 1 polinomunun derecesi nedir? Polinomun geçerli terimlerini inceleyerek derecesini belirleyiniz.
A) 1
B) 2
C) 3
D) 4

Çözüm:
En yüksek dereceli geçerli terim 4x² olduğundan, polinomun derecesi 2’dir. Doğru cevap: B

Soru 8:
P(x) = x² – 4x + 4 polinomunu çarpanlarına ayırarak elde edilen ifade nedir? Polinomu çarpanlarına ayırma yöntemini kullanarak sonucu bulunuz.
A) (x – 2)(x + 2)
B) (x – 2)²
C) (x + 2)²
D) (x – 4)(x + 1)

Çözüm:
P(x) = (x – 2)(x – 2) = (x – 2)². Doğru cevap: B

Soru 9:
Bir polinom, P(x) = 3x² – 2x + 5 olarak veriliyor. Bu polinomun katsayıları toplamı kaçtır? Katsayıların toplamını belirlemek için P(1) değerini kullanınız.
A) 6
B) 7
C) 8
D) 9

Çözüm:
P(1) = 3(1)² – 2(1) + 5 = 3 – 2 + 5 = 6. Doğru cevap: A

Soru 10:
Bir polinom P(x) = x³ – 4x + 4 olarak verilmiştir. Bu polinomun x = 2 kökünü doğrulayınız. Bu kökün polinomun sıfır yapıp yapmadığını kontrol ediniz.
A) 2 köküdür
B) 2 kökü değildir
C) 1 köküdür
D) -2 köküdür

Çözüm:
P(2) = 2³ – 4(2) + 4 = 8 – 8 + 4 ≠ 0, yani x = 2 kök değildir. Doğru cevap: B