Gerçek Sayıların Köklü Gösterimleri İle Yapılan İşlemler (Köklü Sayılar) 9. Sınıf Matematik
Köklü sayılar, bir sayının karesini, küpünü ya da herhangi bir dereceden kökünü ifade etmek için kullanılan matematiksel gösterimlerdir. Bu sayılar, özellikle rasyonel olmayan sayıların gösteriminde ve işlemlerinde büyük öneme sahiptir. Köklü sayılarla yapılan işlemler, köklerin derecelerine, kök içindeki sayılara ve sayıların çarpanlarına göre değişiklik gösterir.
9. Sınıf Gerçek Sayıların Üslü ve Köklü Gösterimleri ile Yapılan İşlemler Konuları (Yeni Müfredat)
- 9. Sınıf Gerçek Sayıların Üslü Gösterimi
- 9. Sınıf Gerçek Sayıların Üslü Gösterimleriyle Yapılan Toplama, Çıkarma, Çarpma ve Bölme İşlemleri
- 9. Sınıf Üslü Gösterimleri Verilen Sayıların Üssünü Alma İşlemi
- 9. Sınıf Gerçek Sayıların Köklü Gösterimi ile Yapılan İşlemler
9. Sınıf Gerçek Sayıların Üslü Gösterimleri ile Yapılan İşlemler Testleri (Yeni Müfredat)
9. Sınıf Gerçek Sayıların Köklü Gösterimleri ile Yapılan İşlemler Testleri (Yeni Müfredat)
9. Sınıf Köklü Gösterimler Tonguç Akademi Video
9. Sınıf Köklü Gösterimler Partikül Matematik Video
9. Sınıf Köklü Gösterimler Rehber Matematik Video
9. Sınıf Gerçek Sayıların Köklü Gösterimleri İle Yapılan İşlemler (Köklü Sayılar – Köklü İfadeler) Ders Notu
Gerçek Sayıların Köklü Gösterimi (Köklü Sayılar – Köklü İfadeler)
n pozitif tam sayı olmak üzere, xⁿ = a eşitliğini sağlayan x sayısına a’nın n’inci dereceden kökü denir.
şeklinde yazılır. Burada n sayısına kökün derecesi denir ve n = 2 olduğunda yazılmaz.
n = 1 ise
n = 2 ise (karekök a)
n = 3 ise (küp kök a)
n = 4 ise (dördüncü dereceden kök a)
şeklinde okunur.
Örneğin;
- 2³ = 8 olduğundan
= 2
- 3⁴ = 81 olduğundan
= 3
- (−2)⁵ = −32 olduğundan
= −2
- (1/2)³ = 1/8 olduğundan
= 1/2 olur.
Bilgi:Kökün gerçek sayı belirtmesi için, kök derecesi çift sayı ise kökün içi negatif olmamalıdır.
Örneğin,
→ gerçek sayıdır.
→ gerçek sayıdır.
→ gerçek sayıdır.
→ gerçek sayı değildir.”
Üslü ve Köklü Gösterimlerin Birbiri Cinsinden İfade Edilmesi
n ∈ Z⁺, n ≥ 2 ve a ∈ R olmak üzere,
- n tek ise
= a
- n çift ise
= |a|
olarak kök dışına çıkarılır.
Örneğin;
= |3| = 3
= |−4| = 4
= |−5| = 5
= -2
= 3
Kural:
Örnek: Aşağıda verilen köklü ifadeleri üslü biçimde yazınız ve çözünüz.
Gerçek Sayıların Köklü Gösterimi (Köklü Sayılar – Köklü İfadeler) Çözümlü Sorular
Köklü Gösterimlerle Toplama, Çıkarma, Çarpma, Bölme ve Kökün Kökünü Alma İşlemleri
Köklü sayılarda toplama ve çıkarma işlemi ortak çarpan parantezine alınarak yapılır.
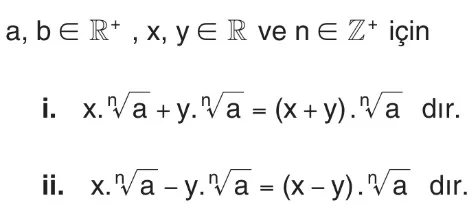
Örnek: Aşağıdaki işlemleri inceleyin.
a)
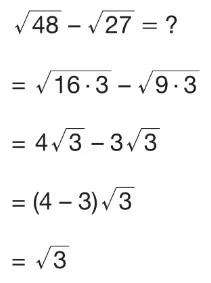
b)
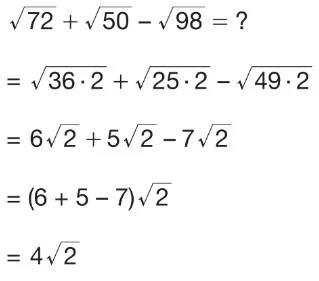
c)
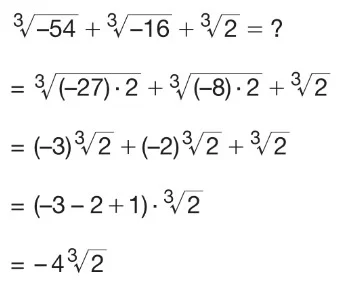
Dereceleri aynı olan iki köklü sayıda çarpma ve bölme işlemi aşağıdaki gibi yapılır. Derecelerin aynı olmadığı durumda önce köklerin dereceleri eşitlenmelidir.


Kural:
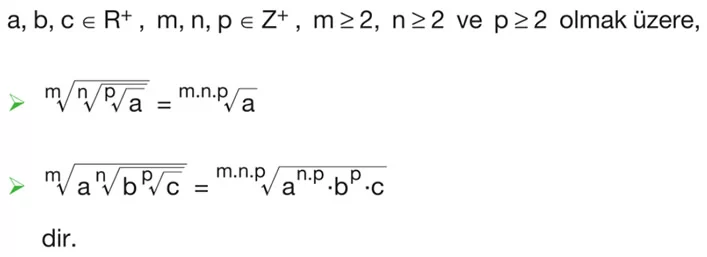
Örnek: Aşağıdaki işlemleri inceleyin.
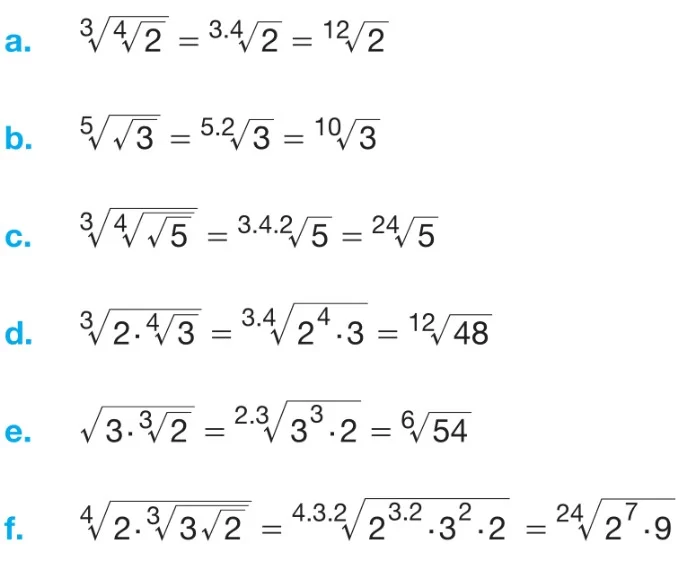
Kural:

Örnek: Aşağıdaki işlemleri inceleyin.
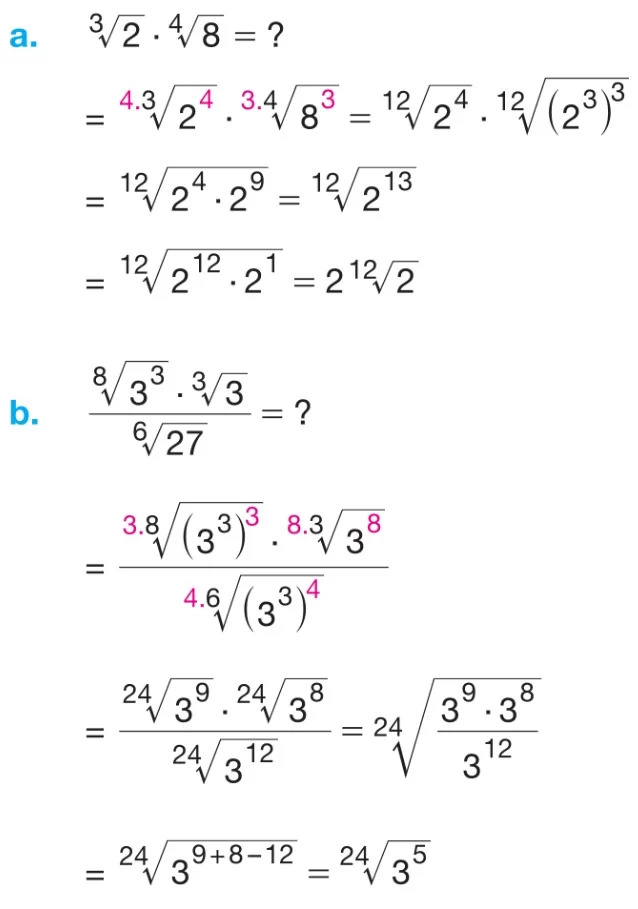
Köklü Gösterimlerle Toplama, Çıkarma, Çarpma, Bölme ve Kökün Kökünü Alma İşlemleri Çözümlü Sorular (Köklü Sayılar – Köklü İfadeler)
Köklü Gösterimlerin (Köklü Sayılar – Köklü İfadeler) Eşleniğini Bulma
Çarpımları rasyonel sayı olan iki köklü ifadeye birbirinin eşleniği denir.

Örnek: Aşağıdaki eşlenik işlemleri inceleyin.

Örnek:

Örnek:

Köklü Gösterimlerin Eşleniğini Bulma Çözümlü Sorular (Köklü Sayılar – Köklü İfadeler)
Köklü Gösterimlerle Yapılan İşlemler Test Soruları ve Çözümlü Örnekler
Çözümlü Örnek Test Soruları
Soru 1:
√75 ifadesini en sade hâlde yazınız.
A) 5√3
B) 15
C) 25
D) 3√5
E) 25√3
Çözüm:
√75 = √(25 * 3) = 5√3
Doğru Cevap: A
Soru 2:
√48 + √12 ifadesinin en sade hâli nedir?
A) 5√3
B) 2√15
C) 6√3
D) 4√3
E) 2√10
Çözüm:
√48 = 4√3 ve √12 = 2√3
Bu durumda: 4√3 + 2√3 = 6√3
Doğru Cevap: C
Soru 3:
√18 – √8 işleminin sonucunu bulunuz.
A) √2
B) 2√2
C) 2√3
D) √10
E) 3√2
Çözüm:
√18 = 3√2 ve √8 = 2√2
Bu durumda: 3√2 – 2√2 = √2
Doğru Cevap: A
Soru 4:
√(27 / 3) ifadesinin sonucu nedir?
A) √9
B) 3
C) 2
D) √3
E) 6
Çözüm:
√(27 / 3) = √9 = 3
Doğru Cevap: B
Soru 5:
√50 ifadesinin 2√2 ile çarpımı kaçtır?
A) 10√2
B) 5√10
C) 10√5
D) 5√2
E) 20
Çözüm:
√50 = 5√2 olduğundan, 5√2 * 2√2 = 10 * 2 = 20
Doğru Cevap: E
Soru 6:
√(3) + √(12) – √(27) işleminin sonucu nedir?
A) √3
B) 2√3
C) 3√3
D) -√3
E) 4√3
Çözüm:
√12 = 2√3 ve √27 = 3√3 olduğuna göre:
√3 + 2√3 – 3√3 = 0
Doğru Cevap: A
Soru 7:
√72 ifadesi ile √18 ifadesinin farkı kaçtır?
A) 4√2
B) 3√2
C) 6√3
D) 2√3
E) 5√3
Çözüm:
√72 = 6√2 ve √18 = 3√2 olduğuna göre:
6√2 – 3√2 = 3√2
Doğru Cevap: B
Soru 8:
(√20 * √5) ifadesinin sonucu nedir?
A) √25
B) 10
C) 5√5
D) 10√5
E) 4√3
Çözüm:
√20 * √5 = √(20 * 5) = √100 = 10
Doğru Cevap: B
Soru 9:
√45 + √20 ifadesinin en sade hâli nedir?
A) 9√5
B) 5√5
C) 7√3
D) 5√3
E) 3√5 + 2√5
Çözüm:
√45 = 3√5 ve √20 = 2√5
Bu durumda: 3√5 + 2√5 = 5√5
Doğru Cevap: B
Soru 10:
√8 / √2 işleminin sonucu nedir?
A) 2
B) 3
C) 4
D) √2
E) 2√2
Çözüm:
√8 / √2 = √(8 / 2) = √4 = 2
Doğru Cevap: A



































GERÇEKTEN ELİNİZE EMEĞİNİZE SAĞLIK
Cok.iyi anladim sagolunnn;)
Tek kelimeyle muhteşem…Gerçekten bu kadar emek vermeniz ve bu kadar zaman harcamanız inanın boşuna gitmiyor.Yani sizin o kadar zaman ayırıp ve büyük bir emek vererek videoları hazırlayıp koşulsuz şartsız bizim önümüze koymanız hiç azımsancak gibi bir durum değil hele ki bu devirde.ALLAH Razı Olsun.Gerçekten çok iyi videolarınız var.Belki de bizim için hayatımızın en önemli zamanında hayatımızın bir dönüm noktasında iken bize bu yardımlarınız gerçekten olağanüstü bir şey.Bunu kelimelere dökemiyorum.Karşılıksız bize en büyük faydayı sağlıyor olmanız bizim için çok büyük bir şey.Çok teşekkur ederim.
Paydada irrasyonel sayı varsa ne yapıyoruz? Eşleniği ile çarpıyoruz. E normal payda eşitleme yaparken de payı da çarpıyoruz ya, o yüzden eşlenik paya da gidiyor. Normalde 2’ye dağıtırsın ama, sadeleşebileceği için bir adım fazla yaparsın, dağıtmadan bi bakarsın. O yüzden ilk başta dağıtmıyorlar. Paydaya gelecek olursak, eşleniği ile çarpıldığından kök5 = 5, kök3= 3 oluyor. Sonra, 5-3’ten payda 2 kalıyor. E payda 2 var, hop sadeleşiyor. Geriye kalan da cevap oluyor.
Hocam detaylı ve anlaşılır bir şekilde bize aktarıyorsunuz. Çok teşekkür ederim 🙂 Yavaş yavaş anlatmanız bizim kafamızda daha çok şekilenmeyi sağlıyor hızlı anlatırsanız anlamayız zaten ki :)