Kümeler 9. sınıf
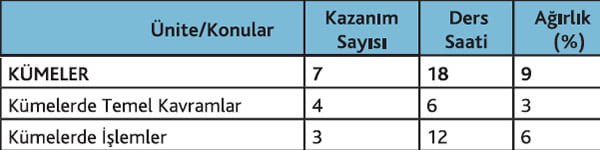
Kümeler konusu 9. sınıf müfredatında ilk sırada yer alan konudur. Aşağıda paylaştığımız resimden de anlaşılacağı üzere toplam 7 kazanımdan oluşuyor. Kümeler konusuna yıllık planda 18 saatlik bir zaman ayrıldığını görüyoruz. Kümeler konusu kendi içinde iki alt başlığa ayrılmaktadır. Kümelerde temel kavramlar konusu 6 saat, Kümelerde işlemler konusu da 12 saat olarak planlanmaktadır. Bu yazımızda daha çok kümeler konusu ile ilgili ders notu paylaşıyoruz. Sadece konunun özü ile ilgili örneklere yer verilecek olup, her konu başlığı ile ilgili ayrıntılı soru çözümü konularını da hazırladığımızda buradan sizlerle paylaşacağız.
9. Sınıf Kümeler Testleri
Kümeler Ders Notları
A. Kümelerde Temel Kavramlar
- Kümeler ile İlgili Temel Kavramlar
→ Kümeler ile İlgili Temel Kavramlar Soru Çözümleri - Alt Küme
→ Alt Küme Soru Çözümleri - Eşit Kümeler ve Soruları
B. Kümelerde İşlemler
- Kümelerde Kesişim ve Birleşim İşlemleri
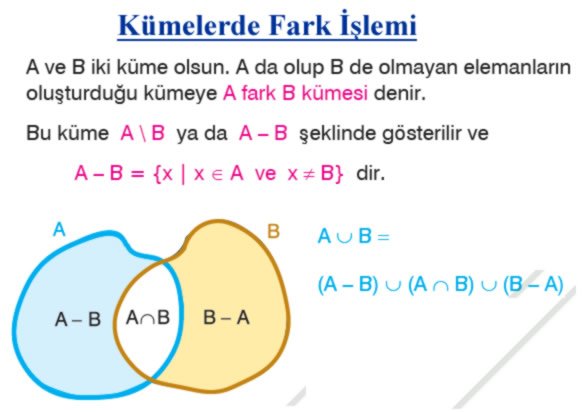
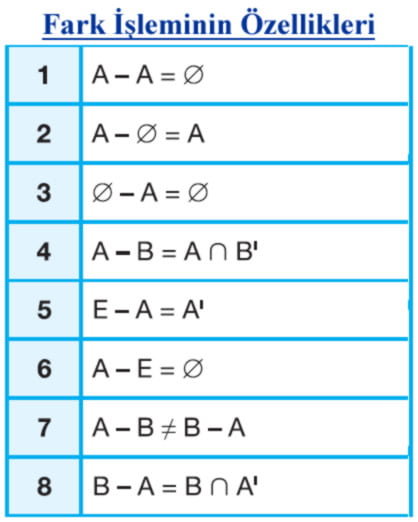
→ Kümelerde Kesişim ve Birleşim İşlemleri Soru Çözümleri - Kümelerde Fark ve Tümleme İşlemleri
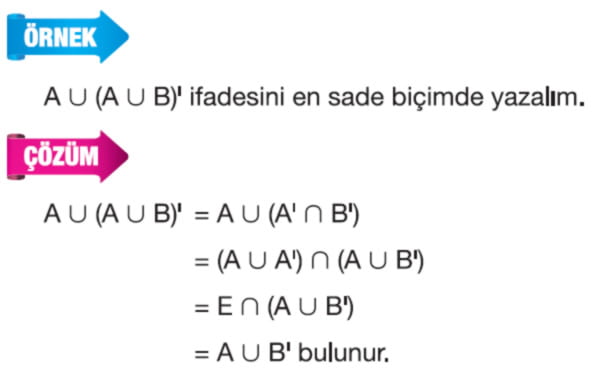
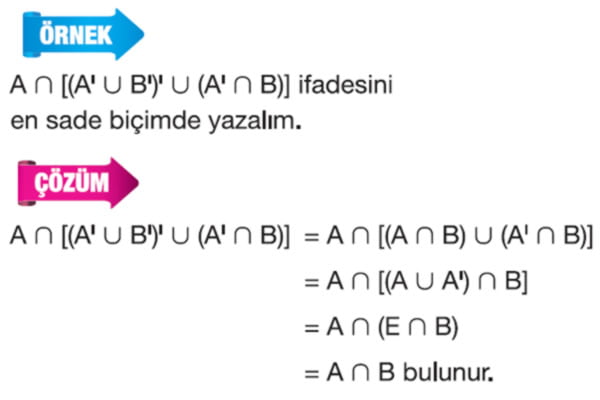
→ Kümelerde Fark ve Tümleme İşlemleri Soru Çözümleri - Küme İşlemleri ile Sembolik Mantık Kuralları Arasındaki İlişki ve Soruları
- Küme Problemleri
→ Küme Problemleri Soru Çözümleri
- İki Kümenin Kartezyen Çarpımı
→ İki Kümenin Kartezyen Çarpımı Soru Çözümleri
Küme Kavramı
Küme, elemanları iyi tanımlanmış nesneler topluluğudur. Kümenin belirlenebilmesi için elemanlarının iyi tanımlanmış olması ve herkes tarafından aynı şekilde anlaşılması gerekir.
Eleman Kavramı, Eleman Sayısı
Bir kümeyi oluşturan nesnelerin her birine o kümenin elemanı denir. Kümeler genellikle A, B. C gibi büyük harflerle isimlendirilir. Bir x elemanı A kümesinin elemanı ise bunu x ∈ A biçiminde yazar ve “x elemanıdır A” diye okuruz. Bir x elemanı A kümesinin elemanı değilse bunu x ∉ A biçiminde yazar ve “x elemanı değildir A” diye okuruz. A kümesinin elemanlarının sayısı s(A) ile gösterilir.
Kümenin tanımı ile ilgili ayrıntılı bilgi ve çözümlü örnekler için buraya tıklayın.
Örnek: “Güzel sözler” cümlesi iyi tanımlı olmadığı için küme belirtmez. Çünkü güzellik herkese göre değişiklik gösterir. birimiz için güzel olan bir resim başka biri için güzel olmayabilir. Aynı şekilde “sınıftaki çalışkan öğrenciler”, “Sıcak günler”, “Uzun boylu öğrenciler” cümleleri de küme belirtmezler.
“4 ile 6 arasındaki doğal sayı” cümlesi iyi tanımlı olduğu için küme belirtir. Çünkü 4 ile 6 arasındaki doğal sayı herkes için 5 tir.
“Yaşayan zeki insanlar” cümlesi iyi tanımlı olmadığı için küme belirtmez. Çünkü zekinin tanımı herkes için aynı değildir.
“1924 sayısının rakamları” cümlesi iyi tanımlı olduğu için küme belirtir.
Küme Gösterim Yöntemleri
Küme gösterimleri matematiğin dilini kurmada önemli bir yere sahiptir. Bir küme 3 farklı şekilde gösterilebilir. Bunlar;
Liste yöntemi, venn şeması (diyagramı) yöntemi ve Ortak özellik yöntemidir.
Küme gösterim yöntemleri nelerdir örnek soru çözümleri için tıklayın.
Örnek: A = {1, 3, 5, 7, 9} kümesinin ortak özellik yöntemiyle gösterelim.
Çözüm: 10 a kadar olan tek doğal sayılar 1, 3, 5, 7, 9 dur. Bu durumda elemanları 1, 3, 5, 7, 9 olan kümenin ortak özellik yöntemi ile gösterimi,
A = {10 a kadar olan tek doğal sayılar} olabilir.
Sonlu ve Sonsuz Kümeler, Boş Küme
Sonlu sayıda elemana sahip kümelere sonlu küme, sonlu olmayan kümelere ise sonsuz küme denir. Hiçbir elemanı olmayan kümelere boş küme denir ve boş küme ∅ veya { } sembolleriyle gösterilir.
Sonlu küme, sonsuz küme, boş küme tanımı ve çözümlü örnekler için tıklayın.
Örnek: Aşağıda verilen kümelerin sonlu, sonsuz veya boş küme olup olmadıklarını inceleyelim.
a) A = {x | x, 2 ile bölünebilen tek doğal sayı}
b) B = {x | x, çift asal sayı}
c) C = {x| 5 < x < 6 ve x doğal sayı}
ç) Ç = {x | x, yılın herhangi bir ayı}
d) D = {x | x > 100 olan bir tam sayı}Çözüm:
a) Tek sayılar 2 ile bölünemeyeceğinden A = ∅
b) Çift olan tek asal sayı 2 dir. Dolayısıyla B = {2} olup sonlu bir kümedir.
c) 5 ile 6 arasında hiçbir doğal sayı bulunmadığından C = ∅
ç) Ç = {Ocak, Şubat, Mart, Nisan, Mayıs, Haziran, Temmuz, Ağustos, Eylül, Ekim, Kasım, Aralık} olup sonlu bir kümedir.
d) D = {101, l02, 103, …} şeklinde sonsuz bir kümedir.
Alt Küme
A ve B herhangi iki küme olsun. A kümesinin her elemanı. B kümesinin de elemanı ise A ya B nin alt kümesi denir. A kümesinin, B kümesinin alt kümesi olduğu A ⊂ B biçiminde gösterilir. A kümesi B kümesinin alt kümesi ise, B kümesi A kümesini kapsar denir ve A ⊃ B biçiminde gösterilir.
Örneğin, A = {1, 2, 3}, B = {1, 2, 3, 4} kümelerinde, A kümesinin her elemanı B kümesinin de elemanı olduğundan A ⊂ B olur.
B kümesinde olup A kümesinde olmayan en az bir eleman varsa “B kümesi A kümesinin alt kümesi değildir.” denir. B kümesi A kümesinin alt kümesi değilse, B ⊄ A biçiminde gösterilir.
Kümelerde İşlemler
Kartezyen Çarpım
İki Kümenin Kartezyen Çarpımı
A ve B boş kümeden farklı iki küme olsun. Birinci bileşeni A kümesinden, ikinci bileşeni B kümesinden alınarak oluşturulan tüm sıralı ikililerin kümesine A ile B nin kartezyen çarpımı denir.
Bu küme A x B şeklinde yazılır ve “A kartezyen çarpım B” şeklinde okunur.
A x B = {(x , y): x ∈ A ve y ∈ B}
B x A = {(x , y): x ∈ B ve y ∈ A}
Küme Problemleri
Kümeler Çözümlü Sorular ve Testler 9. Sınıf
Kümelerle İlgili Temel Kavramlar
- Boş Küme: Elemanı olmayan kümeye boş küme denir ve ∅emptyset ya da { } ile gösterilir.
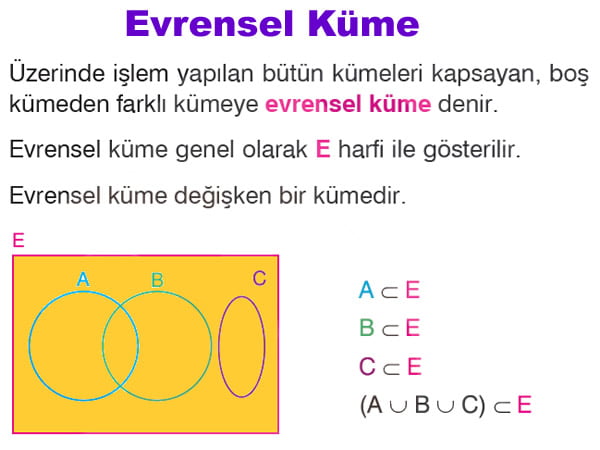
- Evrensel Küme: Çalışılan tüm kümelerin alt kümesi olan kümedir. Genellikle U ile gösterilir.
- Alt Küme: A kümesindeki her eleman B kümesinde de bulunuyorsa, A kümesi B kümesinin alt kümesidir. A ⊆ B olarak gösterilir.
- Kesişim Kümesi: İki kümenin ortak elemanlarının oluşturduğu kümeye denir ve A∩BA ∩ B ile gösterilir.
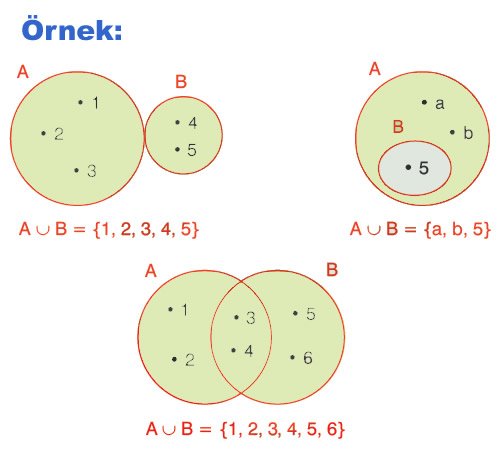
- Birleşim Kümesi: İki kümenin tüm elemanlarının oluşturduğu kümeye denir ve A∪BA ∪ B ile gösterilir.
- Fark Kümesi: A kümesinde olup B kümesinde olmayan elemanların oluşturduğu kümeye denir ve A−BA – B ile gösterilir.
Çözümlü Örnek Test Soruları
Soru 1:
A = {1, 2, 3, 4} ve B = {3, 4, 5, 6} kümeleri veriliyor.
A ∩ B kesişim kümesini bulunuz.
A) {1, 2}
B) {3, 4}
C) {5, 6}
D) {1, 3}
E) {2, 6}
Çözüm:
Kesişim kümesi, iki kümenin ortak elemanlarından oluşur. A ve B kümelerinde ortak olan elemanlar 3 ve 4’tür.
Bu durumda A ∩ B = {3, 4} olur.
Cevap: B
Soru 2:
A = {a, b, c, d} ve B = {c, d, e, f} kümeleri veriliyor.
A ∪ B birleşim kümesini bulunuz.
A) {a, b, c, d}
B) {c, d}
C) {a, b, e, f}
D) {a, b, c, d, e, f}
E) {a, b, c}
Çözüm:
Birleşim kümesi, iki kümedeki tüm elemanlardan oluşur. Aynı olan elemanlar yalnızca bir kez yazılır. A ∪ B = {a, b, c, d, e, f} olur.
Cevap: D
Soru 3:
A = {1, 2, 3, 4, 5} ve B = {3, 4, 6} kümeleri veriliyor.
A – B fark kümesini bulunuz.
A) {1, 2, 5}
B) {3, 4}
C) {1, 6}
D) {2, 3, 5}
E) {1, 5, 6}
Çözüm:
A – B, A kümesinde olup B kümesinde olmayan elemanlar anlamına gelir. A kümesindeki 3 ve 4 elemanları B kümesinde de olduğu için çıkarılır, geriye {1, 2, 5} kalır.
Cevap: A
Soru 4:
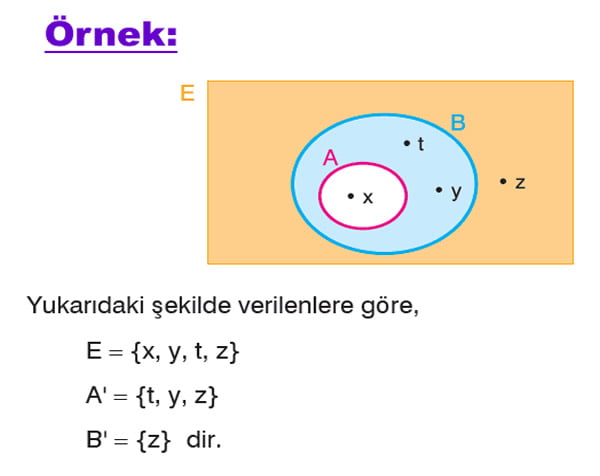
Evrensel küme U = {1, 2, 3, 4, 5, 6, 7} ve A = {2, 4, 6} olduğuna göre, A’nın tümleyeni nedir?
A) {2, 4, 6}
B) {1, 3, 5, 7}
C) {1, 2, 3}
D) {3, 5, 6}
E) {4, 7, 1}
Çözüm:
A’nın tümleyeni, evrensel kümede olup A kümesinde olmayan elemanlardan oluşur. U = {1, 2, 3, 4, 5, 6, 7} ve A = {2, 4, 6} olduğuna göre, A’nın tümleyeni {1, 3, 5, 7} olur.
Cevap: B
Soru 5:
A = {x | x bir asal sayıdır ve x ≤ 10} kümesi aşağıdakilerden hangisidir?
A) {2, 3, 5, 7}
B) {1, 2, 3, 5, 7}
C) {2, 3, 5, 7, 11}
D) {1, 2, 3, 4, 5}
E) {3, 5, 7, 9}
Çözüm:
10’a kadar olan asal sayılar 2, 3, 5 ve 7’dir. Bu nedenle A = {2, 3, 5, 7} olur.
Cevap: A