Kümelerde Birleşim ve Kesişim İşlemleri 9. Sınıf
Kümelerde Birleşim İşlemi
A ve B herhangi iki küme olsun. A ve B kümelerinin tüm elemanlarının oluşturduğu kümeye A ve B kümelerinin “birleşim kümesi” denir. A ve B kümelerinin birleşim kümesi “A ∪ B” ile gösterilir, “A birleşim B” şeklinde okunur.
Kısaca; A ∪ B = {x | x ∈ A veya x ∈ B} dir.
Birleşim İşleminin Özellikleri
Kümelerde Kesişim İşlemi
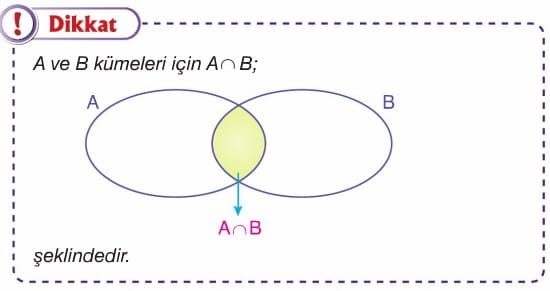
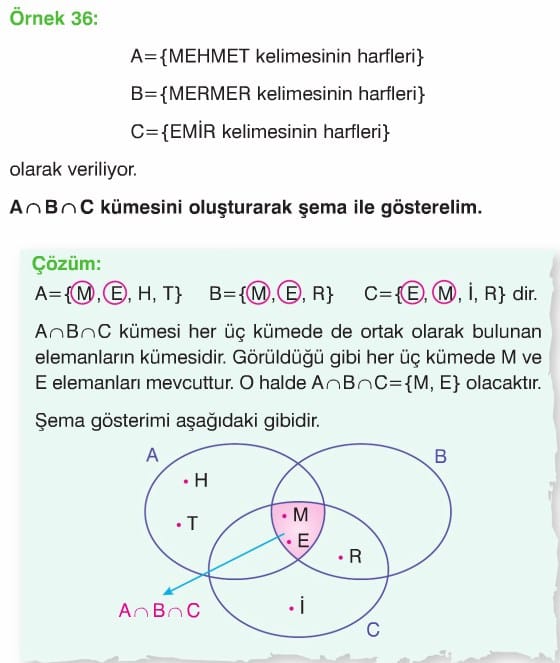
A ve B herhangi iki küme olsun. A ve B kümelerinin ortak elemanlarının oluşturduğu kümeye A ve B kümelerinin “kesişim kümesi” denir. A ve B kümelerinin kesişim kümesi “A ∩ B” ile gösterilir ve “A kesişim B” şeklinde okunur.
Kısaca; A ∩ B = {x | x ∈ A ve x ∈ B} dir.
Kesişim İşleminin Özellikleri
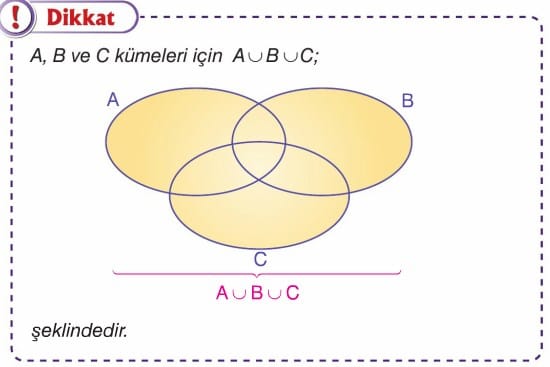
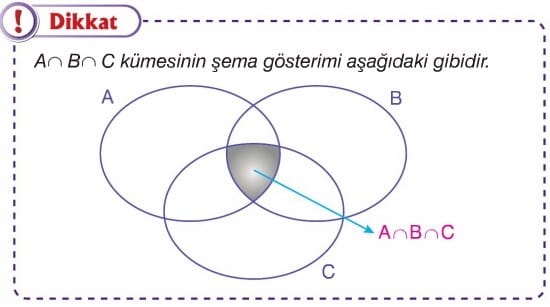
Dikkat: A, B ve C kümeleri için,
- A ∪ (B ∩ C) = (A ∪B) ∩ (A ∪ C) eşitliğine birleşim işleminin kesişim işlemi üzerine “soldan dağılma özelliği” denir.
- A ∩ (B ∪C) = (A ∩ B) ∪ (A ∩ C) eşitliğine kesişim işleminin birleşim işlemi üzerine “soldan dağılma özelliği” denir.
- (A ∩ B) ∪C = (A ∪ C) ∩ (B ∪ C) eşitliğine birleşim işleminin kesişim işlemi üzerine “sağdan dağılma özelliği” denir.
- (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C) eşitliğine kesişim işleminin birleşim işlemi üzerine “sağdan dağılma özelliği” denir.
Birleşim ve Kesişim İşlemleri Çözümlü Sorular
Kümeler Online Testler Tıklayın
Çözümlü Örnek Test Soruları
Soru 1: A = {1, 2, 3} ve B = {3, 4, 5} kümeleri veriliyor. A ∪ B birleşim kümesi nedir?
A) {1, 2, 3}
B) {3, 4, 5}
C) {1, 2, 3, 4, 5}
D) {1, 3, 5}
Cevap: C
Çözüm: A ∪ B birleşim kümesi, her iki kümenin elemanlarını içerir. A ∪ B = {1, 2, 3, 4, 5} olur.
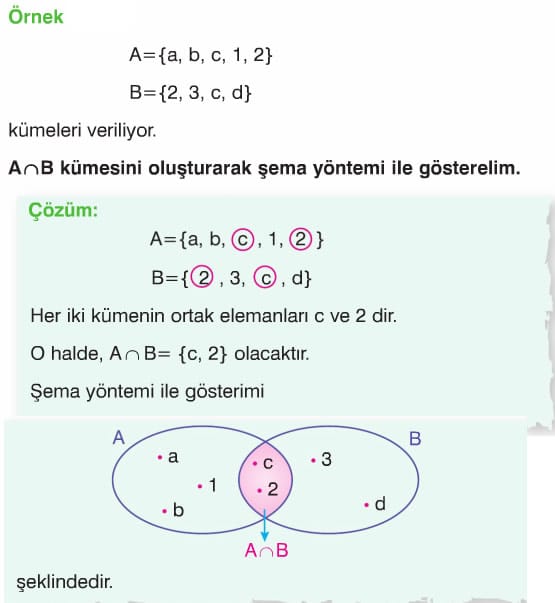
Soru 2: A = {a, b, c} ve B = {b, c, d} kümeleri için A ∩ B kesişim kümesi nedir?
A) {a}
B) {b, c}
C) {a, d}
D) {a, b, c, d}
Cevap: B
Çözüm: A ∩ B kesişim kümesi, her iki kümede ortak olan elemanlardan oluşur. A ∩ B = {b, c} olur.
Soru 3: A = {2, 4, 6, 8} ve B = {4, 5, 6} kümeleri için A ∪ B birleşim kümesi nedir?
A) {2, 4, 5, 6, 8}
B) {4, 6}
C) {2, 5, 8}
D) {2, 4, 6}
Cevap: A
Çözüm: A ∪ B birleşim kümesi, A ve B’nin tüm elemanlarını içerir, yani A ∪ B = {2, 4, 5, 6, 8} olur.
Soru 4: A = {1, 3, 5, 7} ve B = {2, 3, 6, 7} kümeleri için A ∩ B kesişim kümesi nedir?
A) {1, 2, 3, 5, 6, 7}
B) {3, 7}
C) {1, 7}
D) {3, 5}
Cevap: B
Çözüm: A ∩ B kesişim kümesi, her iki kümede ortak olan elemanlardan oluşur, yani A ∩ B = {3, 7} olur.
Soru 5: A = {x | x doğal sayıdır, x < 5} ve B = {3, 4, 5, 6} kümeleri veriliyor. A ∩ B kesişim kümesi nedir?
A) {1, 2, 3, 4}
B) {3, 4}
C) {5, 6}
D) {1, 5}
Cevap: B
Çözüm: A kümesi {0, 1, 2, 3, 4} elemanlarından oluşur. A ve B kümelerinin kesişimi, A ∩ B = {3, 4} olur.
Birleşim işleminin özellikleri: Birleşim işleminin özelliklerini örneklerle açıklayalım.
1) A = {1, 2, 3} ve B = {2, 3, 4} olsun
A ∪ B={1, 2, 3, 4} ve B ∪ A={1, 2, 3, 4}
olacağından A ∪ B = B ∪ A olur. Herhangi iki A ve B kümesi için A ∪ B=B ∪ A eşitliği vardır. Bu eşitliğe “birleşme işleminin değişme özelliği” denir.
2) A = {1, 2, 3} olsun.
A ∪ A = {1, 2, 3} ∪ {1, 2, 3} ={1, 2, 3} = A olur. Bir A kümesi için; A ∪ A = A dır.
3) A = {a, b, c} ve B={ } olsun.
A ∪ B = {a, b, c} ∪ {} = {a, b, c} = A olur. Bir A kümesi için; A ∪ 0 = A dır.
4) A = {1, 2}, B = {3, 4} ve C = {4, 5, 6} olsun.
(A ∪ B) ∪ C = {1, 2, 3, 4} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
A ∪ (B ∪ C) = {1, 2} ∪ {3, 4, 5, 6} = {1, 2, 3, 4, 5, 6} olur.
O halde, (A ∪ B) ∪ C = A ∪ (B ∪ C) yazılabilir. A, B ve C kümeleri için, (A ∪ B) ∪ C = A ∪ (B ∪ C) eşitliği vardır. Bu eşitliğe “birleşme özelliği” denir.
5) A = {a, b, 1}, B={a, b, c, 1, 2} olsun.
A ∪ B={a, b, 1} ∪ {a, b, c, 1, 2} = {a, b, c, 1, 2} = B olur. A alt küme B ise A ∪ B = B dir. Ayrıca; A ∪ B = B oluyorsa, A alt küme B dir.
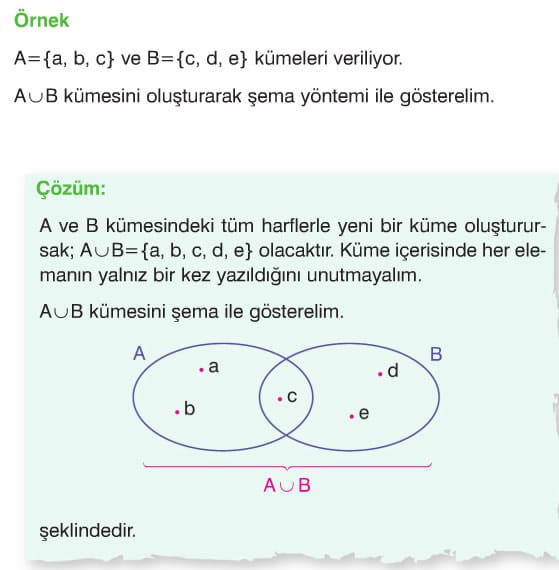
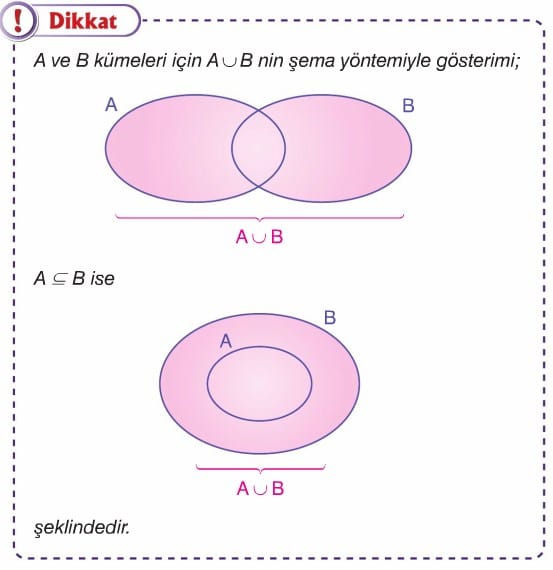
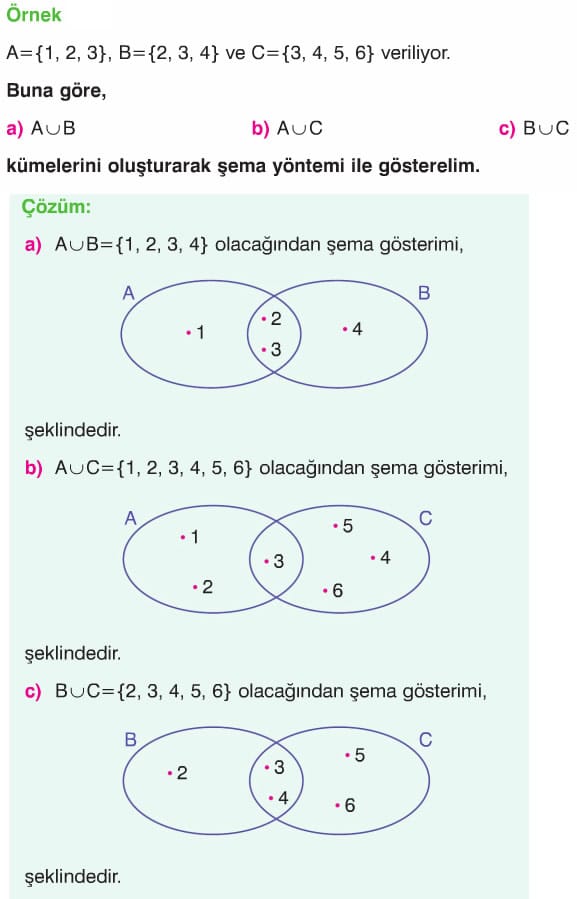
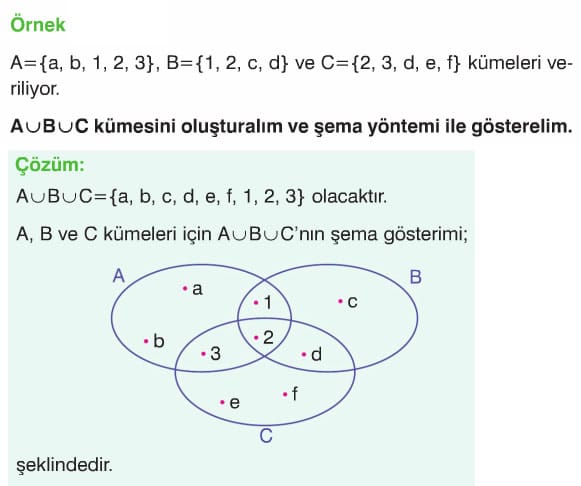

















A birleşim boş küme= boş küme yeri !
Cok iyi anlatmış