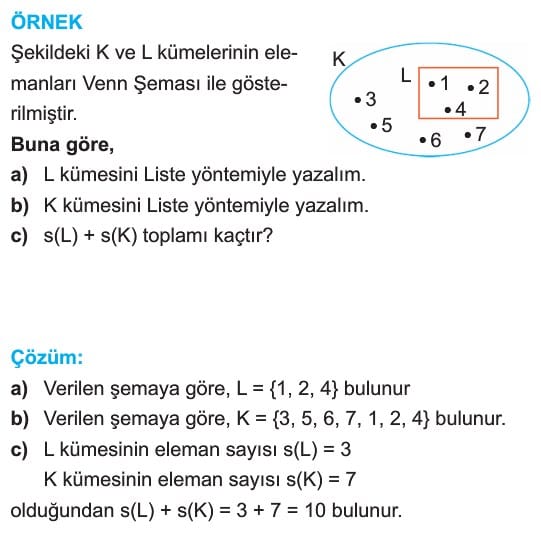
Küme gösterim yöntemleri 9. Sınıf
Üç çeşit küme gösterim yöntemi vardır. Bunlar liste yöntemi, ortak özellik yöntemi ve venn şeması yöntemidir.
1) Liste Yöntemi
Küme elemanlarının, { } biçimindeki bir parantez içine sıra gözetmeksizin, aralarına virgül konularak yazılmasına liste yöntemiyle gösterim denir. Elemanların yer değiştirmesi kümeyi değiştirmez. Örneğin, {1, 2, 3, 4} kümesiyle {3, 4, 1, 2} kümesi aynıdır.
Örnekler:
Aşağıdaki kümeleri liste yöntemiyle gösterelim:
-
“Haftanın p ile başlayan günleri”
Çözüm:A = {pazartesi, perşembe, pazar} -
“Yılın e ile başlayan ayları”
Çözüm:B = {eylül, ekim} -
“MATEMATİK sözcüğündeki harfler”
Çözüm:C = {M, A, T, E, İ, K}
Örnek Çözümü:
A = {1, {1, 2}, 3, {3, 4, 5}, 6} kümesi ile ilgili verilen ifadelerin doğruluğu incelenecektir.
I. 3 ∈ A
-
Doğru, çünkü 3, A kümesinin bir elemanıdır.
II. 2 ∈ A
-
Yanlış, çünkü 2, A kümesinin doğrudan bir elemanı değildir. {1, 2} elemanı A kümesine ait olsa da, bu 2’nin A’nın elemanı olduğu anlamına gelmez.
III. {3, 4, 5} ∈ A
-
Doğru, çünkü {3, 4, 5}, A kümesinin bir elemanıdır.
IV. s(A) = 5
-
Doğru, çünkü A kümesinin elemanları şunlardır:
-
1
-
{1, 2}
-
3
-
{3, 4, 5}
-
6
Toplam 5 eleman bulunmaktadır.
-
Sonuç:
I, III ve IV. ifadeler doğrudur. Doğru cevap: I, III, IV.
2) Venn Şeması Yöntemi
Kümeyi oluşturan nesnelerin kapalı bir eğri (daire, elips, dikdörtgen vb.) içine, önlerine nokta konularak yazılmasına Venn Şeması Yöntemi denir. Bu yöntemde elemanların sırası önemli değildir.
Örnek:
“10’dan küçük çift doğal sayılar” kümesini Venn Şeması ile gösterelim.
Çözüm:
-
Kümenin elemanları belirlenir:
-
10’dan küçük çift doğal sayılar: 0, 2, 4, 6, 8
(Not: Doğal sayılar tanıma göre 0’dan başlayabilir.)
-
-
Bir kapalı eğri (örneğin daire) çizilir ve içine küme elemanları yazılır:
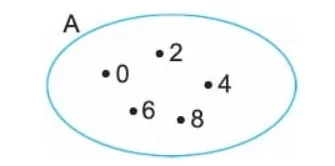
Not:
- Venn şemasında elemanların sırası önemsizdir. Örneğin, 6 ile 8’in yer değiştirmesi şemayı etkilemez.
- Kapalı eğri, kümeyi temsil ettiğinden “A” gibi bir etiketle isimlendirilebilir.
3) Ortak özellik yöntemi
Kümelerin elemanları ortak bir özelliğe sahipse, bu özellik kullanılarak kümenin tanımlanmasına ortak özellik yöntemi denir. Bu yöntem, özellikle eleman sayısı fazla olan kümelerin kısa ve öz şekilde ifade edilmesini sağlar.
Örnek:
Liste yöntemiyle verilen P = {1, 2, 3, 4, …, 99} kümesini ortak özellik yöntemiyle gösterelim.
Kümeler Online Testler Tıklayın
Küme Gösterim yöntemleri çözümlü sorular:
Çözümlü Örnek Test Soruları: Küme Gösterim Yöntemleri
Soru 1: A kümesi {x | x bir doğal sayı ve x < 5} şeklinde ifade edilmiştir. A kümesinin elemanlarını liste yöntemiyle gösteriniz.
- A) {1, 2, 3, 4}
- B) {5, 6, 7, 8}
- C) {0, 1, 2, 3, 4}
- D) {2, 3, 4, 5}
Cevap: C
Çözüm: A kümesinin elemanları, 5’ten küçük doğal sayılardır. Bu durumda A kümesi {0, 1, 2, 3, 4} şeklindedir.
Soru 2: B kümesi {2, 4, 6, 8, 10} olarak verilmiştir. Bu kümeyi ortak özellik yöntemiyle nasıl ifade edebiliriz?
- A) B = {x | x tek bir doğal sayıdır}
- B) B = {x | x 2’den büyük ve 10’dan küçük}
- C) B = {x | x çift bir doğal sayıdır ve 10’dan küçük ya da eşit}
- D) B = {x | x bir asal sayıdır}
Cevap: C
Çözüm: B kümesi, 10’a kadar olan çift doğal sayılardan oluşmaktadır, bu yüzden ortak özellik yöntemiyle {x | x çift bir doğal sayıdır ve 10’dan küçük ya da eşit} olarak ifade edilir.
Soru 3: C = {x | x ∈ Z, -3 ≤ x ≤ 3} kümesinin liste yöntemiyle gösterimi aşağıdakilerden hangisidir?
- A) {0, 1, 2, 3}
- B) {-3, -2, -1, 0, 1, 2, 3}
- C) {1, 2, 3}
- D) {0, 1, 2}
Cevap: B
Çözüm: C kümesi, -3 ile 3 arasındaki tam sayılardan oluşur. Bu durumda C = {-3, -2, -1, 0, 1, 2, 3} olarak listelenir.
Soru 4: A = {1, 3, 5, 7} kümesini Venn şeması ile göstermek için hangi ifadeye ihtiyaç duyarız?
- A) A kümesi doğal sayılardan oluşur.
- B) A kümesi tek sayılardan oluşur.
- C) A kümesi negatif sayılardan oluşur.
- D) A kümesi çift sayılardan oluşur.
Cevap: B
Çözüm: A kümesindeki tüm elemanlar tek sayılardır, bu nedenle A kümesi tek sayılardan oluşmaktadır.
Soru 5: D kümesi {a, e, i, o, u} kümesidir. D kümesini sembolik gösterim yöntemiyle ifade ediniz.
- A) D = {x | x bir sessiz harftir}
- B) D = {x | x bir ünlü harftir}
- C) D = {x | x bir doğal sayıdır}
- D) D = {x | x pozitif bir tam sayıdır}
Cevap: B
Çözüm: D kümesi Türkçedeki ünlü harfleri içerdiğinden {x | x bir ünlü harftir} olarak ifade edilebilir.
Soru 6: E = {x | x 5’in katı olan doğal sayılar} olarak tanımlanmıştır. E kümesinin ilk 4 elemanını liste yöntemiyle gösteriniz.
- A) {5, 10, 15, 20}
- B) {1, 5, 10, 15}
- C) {5, 10, 15, 25}
- D) {0, 5, 10, 15}
Cevap: A
Çözüm: E kümesi, 5’in katı olan doğal sayılardan oluşur. İlk dört elemanı {5, 10, 15, 20} şeklindedir.
Soru 7: F kümesi boş küme olarak verilmiştir. F kümesini liste yöntemiyle nasıl gösterebiliriz?
- A) {0}
- B) {}
- C) {∅}
- D) {1}
Cevap: B
Çözüm: Boş kümenin liste yöntemiyle gösterimi boş bir küme parantezi, yani {} şeklindedir.
Soru 8: G = {x | x asal bir sayı ve x ≤ 10} kümesini liste yöntemiyle gösteriniz.
- A) {1, 2, 3, 5, 7}
- B) {2, 3, 5, 7}
- C) {1, 3, 5, 7, 9}
- D) {2, 4, 6, 8, 10}
Cevap: B
Çözüm: G kümesi 10’dan küçük veya eşit olan asal sayılardan oluşur, yani {2, 3, 5, 7} şeklindedir.
1) Liste Yöntemi: Kümenin tüm elemanları küme parantezi içerisinde virgülle ayrılarak yazılır.
Örnek: 6 dan küçük olan doğal sayıların kümesini liste yöntemi ile gösterelim.
Çözüm: A ={ 0, 1, 2, 3, 4, 5 }
2) Ortak özellik yöntemi: Elemanların ortak özellikleri, küme parantezinin içerisine yazılır.
Örnek: 18 den küçük olan asal sayıların kümesini ortak özellik yöntemi ile gösterelim.
Çözüm: A={ x : x asal sayı ve x<17 }
Örnek: 5 ten küçük olandoğal sayıların kümesini ortak özellik yöntemi ile gösterelim.
Çözüm: A={ x : x < 5 , x ∈ N }
3) Venn şeması yöntemi: Kümenin elemanları kapalı bir eğri içerisine önlerine bir nokta konularak yazılırlar.
Kümedeki tüm elemanların niteliklerini belirten ortak bir söylemle ifade edilmesine ortak özellik yöntemi denir. 10 dan küçük asal sayılar şeklinde ifade edilen kümeyi A={2,3,5,7} şeklinde gösterebiliriz. Örnek: A kümesinin venn diyagramı ile gösterimi aşağıdakilerden hangisidir. A={0, 2, 4, 6, 8, 10} kümesini ortak özellik yöntemi ile gösteriniz. 23102456 sayısındaki rakamların oluşturduğu B kümesi aşağıdakilerden hangisi ile gösterilemez. 10 dan küçük olan sayma sayıları kümesinin elemanlarının sayısal değerlerinin toplamı kaçtır. Şekilde venn şeması yöntemi ile A kümesi verilmiştir. Buna göre aşağıda verilenlerden hangisi yanlıştır.








venn şeması yokkk
deyil var her halde sen görmedin
Eline sağlık
venn şeması yokkk