Soruları anlamakta zorlanıyorsanız İki Kümenin Kartezyen Çarpımı Konu Anlatımı yazımıza giderek konu anlatımına bakabilirsiniz.

Sıralı İkili ve Kartezyen Çarpım Online Testler

9. Sınıf Sıralı İkili ve Kartezyen Çarpım Test 1 Çöz

9. Sınıf Sıralı İkili ve Kartezyen Çarpım Test 2 Çöz

Sıralı İkili ve Kartezyen Çarpım Çözümlü Sorular

Çözümlü Örnek Test Soruları: Sıralı İkili ve Kartezyen Çarpım

1. A = {1, 2} ve B = {3, 4} kümeleri veriliyor. A x B Kartezyen çarpım kümesini bulunuz.

• A) {(1, 3), (1, 4), (2, 3), (2, 4)}
• B) {(1, 2), (3, 4)}
• C) {(3, 1), (4, 1), (3, 2), (4, 2)}
• D) {(1, 4), (2, 4)}

Çözüm: A x B, A kümesindeki her eleman ile B kümesindeki her elemanın sıralı ikililer oluşturulmasıdır. Doğru yanıt A şıkkıdır.

2. A = {a, b} ve B = {1, 2, 3} kümeleri veriliyor. A x B Kartezyen çarpım kümesindeki eleman sayısı kaçtır?

• A) 5
• B) 4
• C) 6
• D) 8

Çözüm: A x B kümesinin eleman sayısı |A| x |B| şeklinde bulunur. |A| = 2 ve |B| = 3 olduğu için 2 x 3 = 6 eleman vardır. Doğru yanıt C şıkkıdır.

3. A = {0, 1} ve B = {x, y} kümeleri için B x A kümesi elemanlarından hangisi doğrudur?

• A) (0, x)
• B) (y, 1)
• C) (1, y)
• D) (x, 0)

Çözüm: B x A ifadesinde ilk bileşen B kümesinden, ikinci bileşen A kümesinden alınır. (y, 1) doğru formattadır. Doğru yanıt B şıkkıdır.

4. A = {3, 4} ve B = {5, 6, 7} kümeleri için A x B Kartezyen çarpımındaki sıralı ikili sayısı kaçtır?

• A) 5
• B) 6
• C) 8
• D) 9

Çözüm: Kartezyen çarpımdaki eleman sayısı |A| x |B| olarak hesaplanır. |A| = 2 ve |B| = 3 olduğundan 2 x 3 = 6 olur. Doğru yanıt B şıkkıdır.

5. A = {1, 2} ve B = {3, 4} kümeleri için A x B kümesindeki (2, 4) sıralı ikilisine karşılık gelen eleman hangisidir?

• A) (1, 3)
• B) (2, 3)
• C) (2, 4)
• D) (1, 4)

Çözüm: (2, 4) sıralı ikilisi, A kümesinden 2 ve B kümesinden 4 elemanını alarak oluşturulur. Doğru yanıt C şıkkıdır.

6. A = {a, b} ve B = {1} kümeleri veriliyor. A x B kümesi hangisidir?

• A) {(a, 1), (b, 1)}
• B) {(1, a), (1, b)}
• C) {(a, b)}
• D) {(1, 1)}

Çözüm: A x B, A kümesindeki her eleman ile B kümesindeki elemanın sıralı ikili olarak birleşimidir: {(a, 1), (b, 1)}. Doğru yanıt A şıkkıdır.

7. A ve B kümeleri için |A| = 3 ve |B| = 4 veriliyor. A x B Kartezyen çarpımının eleman sayısı nedir?

• A) 7
• B) 12
• C) 6
• D) 4

Çözüm: Eleman sayısı |A| x |B| ile bulunur. 3 x 4 = 12 eleman vardır. Doğru yanıt B şıkkıdır.

8. A = {x, y} ve B = {2, 3} kümeleri veriliyor. A x B’de kaç farklı sıralı ikili bulunur?

• A) 2
• B) 3
• C) 4
• D) 5

Çözüm: |A| x |B| = 2 x 2 = 4 farklı sıralı ikili vardır. Doğru yanıt C şıkkıdır.

9. A = {1} ve B = {x, y, z} kümeleri için B x A kümesindeki sıralı ikililerden biri nedir?

• A) (1, x)
• B) (x, 1)
• C) (y, y)
• D) (z, z)

Çözüm: B x A kümesindeki bir eleman B’den ve A’dan sırayla alınır. (x, 1) bu formata uygundur. Doğru yanıt B şıkkıdır.

10. A = {5} ve B = {a, b} kümeleri veriliyor. A x B kümesindeki elemanlardan biri hangisidir?

• A) (a, 5)
• B) (b, 5)
• C) (5, b)
• D) (5, 5)

Çözüm: A x B’de ilk eleman A’dan, ikinci eleman B’den alınır. (5, b) bu kurala uygundur. Doğru yanıt C şıkkıdır.

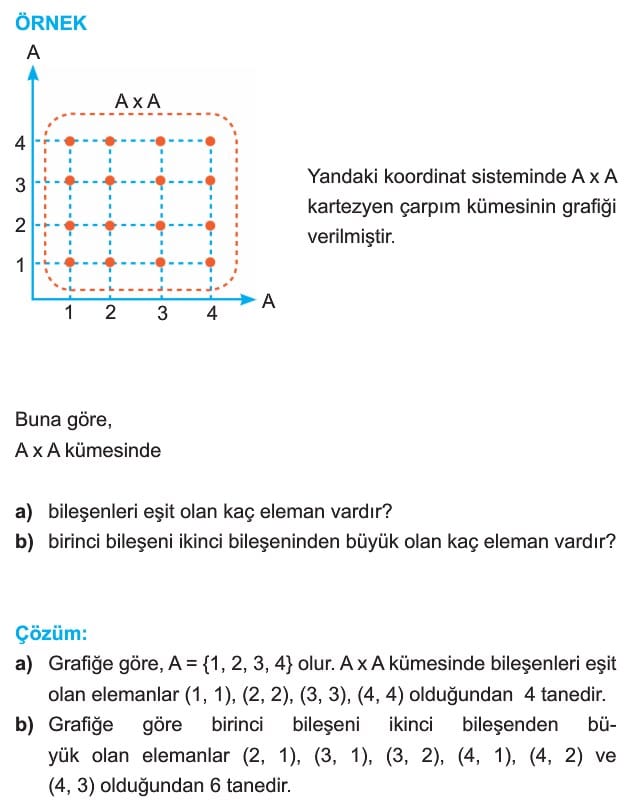
Kartezyen Çarpım: Boş kümeden farklı A ve B kümeleri verilsin. Birinci bileşeni A kümesinden, ikinci bileşeni B kümesinden alınarak oluşturulan tüm sıralı ikililerin kümesine A ve B kümelerinin kartezyen çarpımı denir. A x B” şeklinde gösterilir ve “A kartezyen B” diye okunur.
Kısaca; A x B={(x, y) | elemanıdır  A ve y elemanıdır  B} dir.

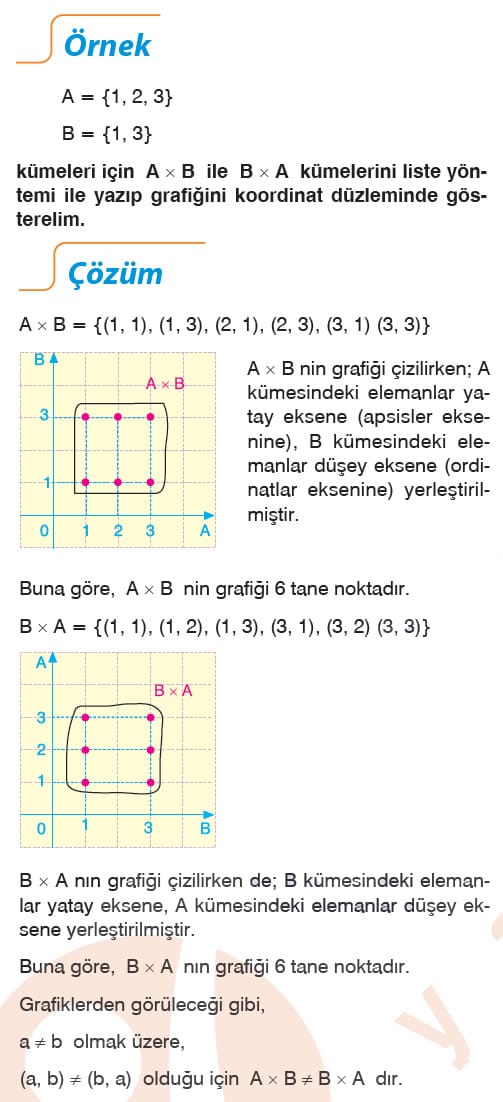
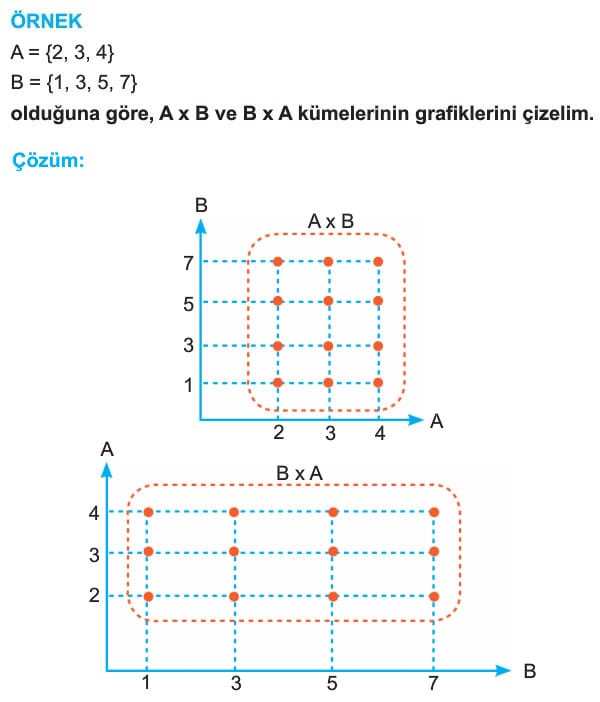
Örnek: A = {1, 2} ve B = {4, 5} kümeleri veriliyor. A x B kümesini oluşturalım.
Çözüm: A x B kümesi, birinci bileşeni A dan, ikinci bileşeni B den alınarak oluşturulan tüm sıralı ikililerden elde edileceğinden,
A x B={(1, 4), (1, 5), (2, 4), (2, 5)} olacaktır.

Örnek: A = {a, b, c} ve B = {2, 3} kümeleri veriliyor. A x B ve B x A kümelerini oluşturalım.
Çözüm: A = {a, b, c} ve B = {2, 3} olduğundan,
A x B = {(a, 2), (a, 3), (b, 2), (b, 3), (c, 2), (c, 3)}
B x A = {(2, a), (2, b), (2, c), (3, a), (3, b), (3, 6)} olacaktır.
Yukarıdaki örnekte görüldüğü gibi A x B, ile B x A kümeleri farklı kümelerdir. Ayrıca A x B ve B x A kümelerinin eleman sayıları eşit ve 6 dır. Kartezyen çarpımının eleman sayısı kümelerin eleman sayılarının çarpımına eşittir.

Örnek: A={x | x < 10, x elemanıdır N)
B={x | 5 küçük eşit x küçük eşit 11, x doğal sayı} kümeleri veriliyor. Buna göre, s(AxB) kaçtır?
A) 60 B) 64 c) 66 D) 70 E) 77
Çözüm: A={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} olacağından s(A)=11
B={5, 6, 7, 8, 9, 10, 11} olacağından s(B)=7 dir. 0 halde, s(AxB)=s(A).s(B)=11.7 = 77 olacaktır. Doğru cevap “E” seçeneğidir.

Örnek: A ve B kümeleri için s(A)=5 ve s(AxB)=20 eşitlikleri verilmiştir. Buna göre, B kümesi aşağıdakilerden hangisi olabilir?
A){1,2} B) (2, 3, 4} C) {a,b,1,2}
D) (2, 3, a} E) {1, 2, 3, b, c}
Çözüm: s(AxB)=s(A).s(B) olacağından verilen eşitlikler yerine yazılırsa, s(AxB)=s(A).s(B)
20=5.s(B) ise s(B)=4 olur. O halde, B kümesi 4 elemanlı bir küme olmalıdır. Dolayısıyla şıklarda 4 elemanlı yalnızca {a, b, 1, 2} kümesi vardır. Doğru cevap “C” seçeneğidir.

Örnek: A, B ve C kümeleri için, s(AxB)=9, s(AxC)=6 olduğuna göre, s(AuBuc) nin alabileceği en büyük değer kaçtır?
A)8 B)9 c)12 D)15 E)16
Çözüm: s(AxB)=s(A).s(B)=9
s(AxC)=s(A).s(C)=6 dır.
s(A)=1 alınırsa, s(B)=9 ve s(C)=6 olacaktır.
s(AuBuC) nin en büyük olabilmesi için A, B ve C kümelerini ayrık küme gibi düşünebiliriz.
O halde, s(AuBuC)=1+9+6=16 olur.
Doğru cevap “E” seçeneğidir.