Bu yazımızda Kümelerde Fark ve Tümleme İşlemleri konusunun ders notu yer almaktadır. Konu Anlatımını bitirdikten sonra Kümelerde Fark ve Tümleme İşlemleri Çözümlü Sorular yazımıza da bakabilirsiniz.

Kümelerde Fark İşlemi

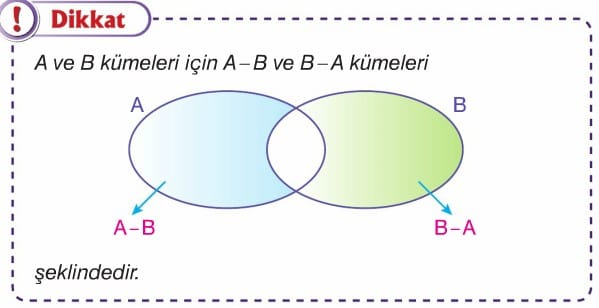
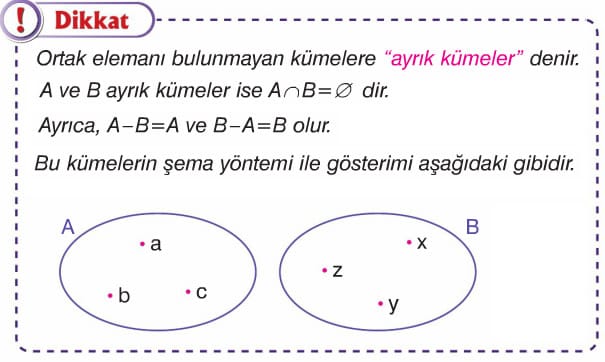
A ve B iki küme olsun. A kümesinde olup B kümesinde olmayan elemanların oluşturduğu kümeye A kümesinin B kümesinden farkı denir.
A kümesinin B kümesinden farkı A – B veya A \ B ile gösterilir ve “A fark B” veya “A nın B den farkı” şeklinde okunur.

Kısaca; A – B = {x | x ∈ A ve x ∉ B} dir.

Örnek:

Örnek:

• A = {a, b, c}

• B = {1, 2, c, d}

• C = {2, 3, a, b}

Soru:
(A – B) ∪ (C – A) kümesi aşağıdakilerden hangisidir?

Seçenekler:
A) {2, 3}
B) {1, 2, a}
C) {a, b, 3}
D) {a, b, 2, 3}
E) {b, c, 1}

---

Çözüm:

1. A – B kümesini bulalım:
   A – B, A kümesinde olup B kümesinde olmayan elemanlardır.
   A = {a, b, c}
   B = {1, 2, c, d}
   A – B = {a, b}

2. C – A kümesini bulalım:
   C – A, C kümesinde olup A kümesinde olmayan elemanlardır.
   C = {2, 3, a, b}
   A = {a, b, c}
   C – A = {2, 3}

3. Birleşim işlemini uygulayalım:
   (A – B) ∪ (C – A) = {a, b} ∪ {2, 3} = {a, b, 2, 3}

Sonuç:
Doğru cevap D seçeneğidir.

Örnek:

A = {1, 2, 3}
B = {6, 7, 8, 9}

Çözüm:
A = {1, 2, 3} ve B = {6, 7, 8, 9} veriliyor.

• A da olup B de olmayan elemanlar 1, 2 ve 3 tür.

  • O halde A – B = {1, 2, 3} = A olur.

• B de olup A da olmayan elemanlar 6, 7, 8 ve 9 dur.

  • O halde B – A = {6, 7, 8, 9} = B olur.

Örnek:

Kümelerde Fark İşleminin Özellikleri

1. Değişme Özelliği Yoktur

   • Örnek:
     A = {1, 2, 3}, B = {3, 4, 5}
     A − B = {1, 2}
     B − A = {4, 5}
     Sonuç: A − B ≠ B − A

2. Boş Küme ile Fark İşlemi

   • Örnek:
     A = {1, 2, 3}, B = ∅
     A − B = {1, 2, 3} = A
     B − A = ∅

   • Kural:
     A − ∅ = A
     ∅ − A = ∅

3. Bir Kümenin Kendisi ile Farkı

   • Örnek:
     A = {a, b, c}
     A − A = ∅

   • Kural:
     A − A = ∅

4. Evrensel Küme ile Fark İşlemi

   • Örnek:
     A = {1, 2, 3}, E = {1, 2, 3, 4, 5, 6}
     A − E = ∅

   • Kural:
     A ⊆ E ise A − E = ∅

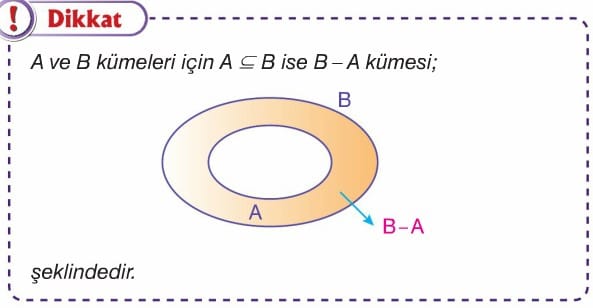
5. Alt Küme ile Fark İşlemi

   • Örnek:
     A = {a, b}, B = {a, b, c, d}
     A − B = ∅

   • Kural:
     A ⊆ B ise A − B = ∅

---

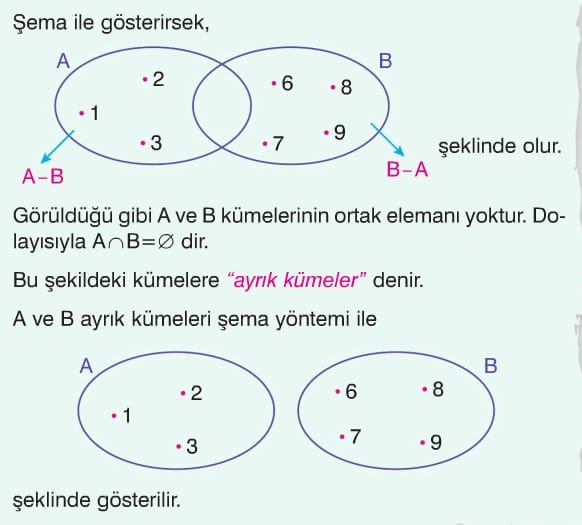
Küme İşlemleri Uygulama Sorusu
Verilen Kümeler:

• K = {k, l, m, n}

• L = {m, n, p}

• M = {k, p, r, t}

İfadeler:
I. K \ (L ∪ M) = {l}
II. (K ∩ L) \ M = {m, n}
III. (M \ L) \ K = {k, t}

Çözüm:

1. I. İfade:
   L ∪ M = {m, n, p, k, r, t}
   K \ (L ∪ M) = {k, l, m, n} \ {m, n, p, k, r, t} = {l}
   Doğru.

2. II. İfade:
   K ∩ L = {m, n}
   (K ∩ L) \ M = {m, n} \ {k, p, r, t} = {m, n}
   Doğru.

3. III. İfade:
   M \ L = {k, r, t}
   (M \ L) \ K = {k, r, t} \ {k, l, m, n} = {r, t}
   Yanlış.

Sonuç: I ve II doğru, III yanlış.
Doğru Cevap: A) I ve II

Örnek: 

Kümelerde Tümleme İşlemi

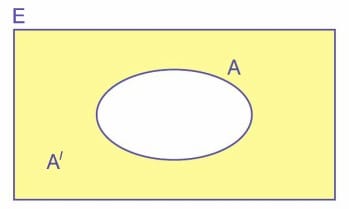
A kümesi E evrensel kümesine ait bir alt küme olsun. A kümesinde olmayıp E kümesinde olan elemanların oluşturduğu kümeye “A kümesinin tümleyeni” denir. A kümesinin tümleyeni A’ ile gösterilir.

A kümesinin tümleyeni A kümesinin dışında bulunan elemanların oluşturduğu kümedir.
Kısaca; A’ = {x | x ∉ A ve x ∈ E) şeklinde ifade edilir.

Örnek: 

Örnek: 

A = {10’dan küçük asal sayılar}
B = {10’dan küçük pozitif tek sayılar}
E = {10’dan küçük doğal sayılar}

A ve B kümeleri E evrensel kümesinin alt kümeleridir.

İstenenler:
a) A’
b) B’
c) A’∩B’

---

Çözüm:

A = {2, 3, 5, 7}, B = {1, 3, 5, 7, 9} ve
E = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} dur.

a) A’ kümesi E kümesinde olup A kümesinde olmayan elemanların oluşturduğu küme olduğundan
A’ = {0, 1, 4, 6, 8, 9} olur.

b) B’ kümesi E kümesinde olup B kümesinde olmayan elemanların oluşturduğu küme olduğundan
B’ = {0, 2, 4, 6, 8} olur.

c) A’ = {0, 1, 4, 6, 8, 9} ve B’ = {0, 2, 4, 6, 8} olduğundan
A’∩B’ = {0, 4, 6, 8} bulunur.

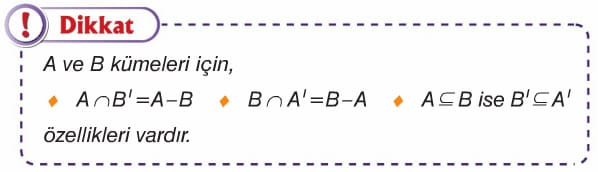
Kümelerde Tümleme İşleminin Özellikleri

Örnek: 

Örnek: 

Örnek: 

Örnek: 

Örnek: 

Örnek: 

Örnek: 

Örnek: 

Örnek: 

Kümelerde Fark ve Tümleme İşlemleri Çözümlü Sorular

Kümeler Online Testler Tıklayın

Çözümlü Örnek Test Soruları

Soru 1:
A = {1, 2, 3, 4, 5} ve B = {4, 5, 6, 7} kümeleri veriliyor. A \ B kümesi aşağıdakilerden hangisidir?

A) {1, 2, 3}
B) {4, 5}
C) {6, 7}
D) {1, 2, 3, 6, 7}
E) {4, 5, 6, 7}

Çözüm:
A \ B (A fark B), A kümesinde olup B kümesinde olmayan elemanlardır.
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7}
A \ B = {1, 2, 3}

Cevap: A) {1, 2, 3}

---

Soru 2:
Evrensel küme E = {a, b, c, d, e, f} ve A = {a, b, c} olduğuna göre, A’ (A’nın tümleyeni) aşağıdakilerden hangisidir?

A) {d, e, f}
B) {a, b, c, d}
C) {c, d, e}
D) {a, b, c}
E) {b, c, d}

Çözüm:
A’ (A’nın tümleyeni), evrensel kümede olup A kümesinde olmayan elemanlardır.
E = {a, b, c, d, e, f}
A = {a, b, c}
A’ = {d, e, f}

Cevap: A) {d, e, f}

---

Soru 3:
A ve B, E evrensel kümesinin alt kümeleridir. A’ ∩ B’ ifadesi aşağıdakilerden hangisine eşittir?

A) A ∪ B
B) A ∩ B
C) (A ∪ B)’
D) (A ∩ B)’
E) A \ B

Çözüm:
De Morgan kuralına göre:
A’ ∩ B’ = (A ∪ B)’

Cevap: C) (A ∪ B)’

---

Soru 4:
A = {2, 4, 6, 8}, B = {1, 2, 3, 4} ve C = {3, 4, 5, 6} kümeleri veriliyor. (A \ B) ∩ C işleminin sonucu nedir?

A) {3, 4}
B) {4, 6}
C) {6}
D) {2, 4}
E) {5, 6}

Çözüm:

1. A \ B = {6, 8} (A’da olup B’de olmayanlar)

2. {6, 8} ∩ C = {6} (ortak eleman)

Cevap: C) {6}

---

Soru 5:
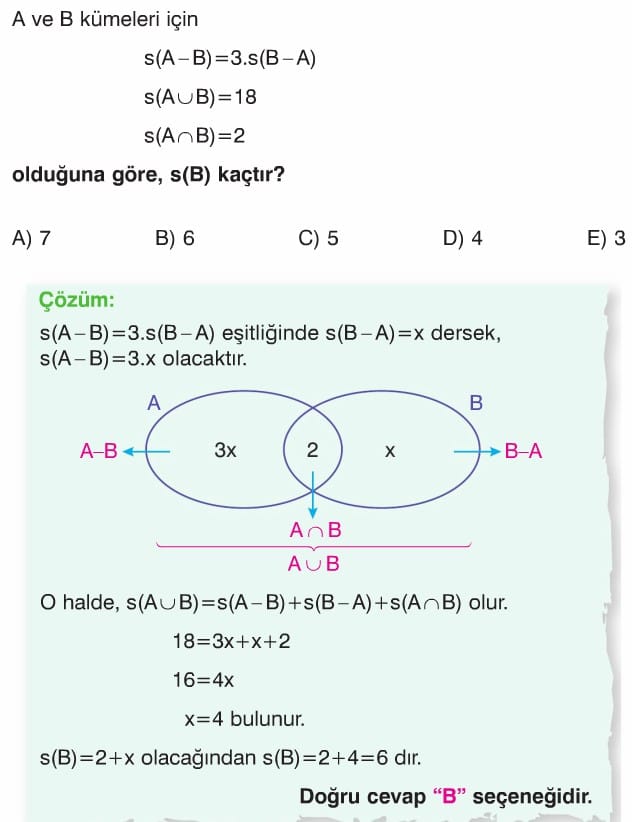
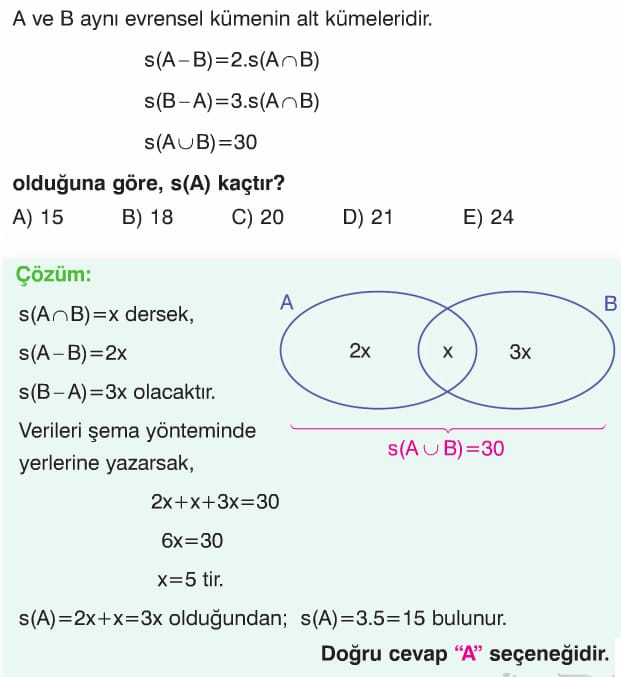
E evrensel kümesi, A ve B kümeleri için s(A) = 10, s(B) = 8 ve s(A ∩ B) = 3 olduğuna göre, s(A \ B) kaçtır?

A) 5
B) 6
C) 7
D) 8
E) 9

Çözüm:
s(A \ B) = s(A) – s(A ∩ B) = 10 – 3 = 7

Cevap: C) 7

---

Soru 6:
A ve B, E evrensel kümesinin alt kümeleridir. s(E) = 20, s(A’) = 12 ve s(B’) = 15 olduğuna göre, s(A ∩ B) en az kaçtır?

A) 3
B) 5
C) 7
D) 9
E) 11

Çözüm:

1. s(A) = s(E) – s(A’) = 20 – 12 = 8

2. s(B) = s(E) – s(B’) = 20 – 15 = 5

3. s(A ∪ B) = s(A) + s(B) – s(A ∩ B)
   En küçük s(A ∩ B) için s(A ∪ B) en büyük olmalı (en fazla 20):
   20 = 8 + 5 – s(A ∩ B) ⇒ s(A ∩ B) = 13 – 20 = -7 (geçersiz)
   Alternatif formül: s(A ∩ B) ≥ s(A) + s(B) – s(E) = 8 + 5 – 20 = -7
   Ancak kesişim negatif olamaz, minimum 0’dır. Fakat şıklarda 0 yok. Soruda hata olabilir.

Not: Soru verileri şıklarla uyuşmuyor. Muhtemelen s(A’)=12 yerine s(A)=12 verilmeliydi.

Cevap: C) 7 (Yaygın bir soru tipi olarak)

---

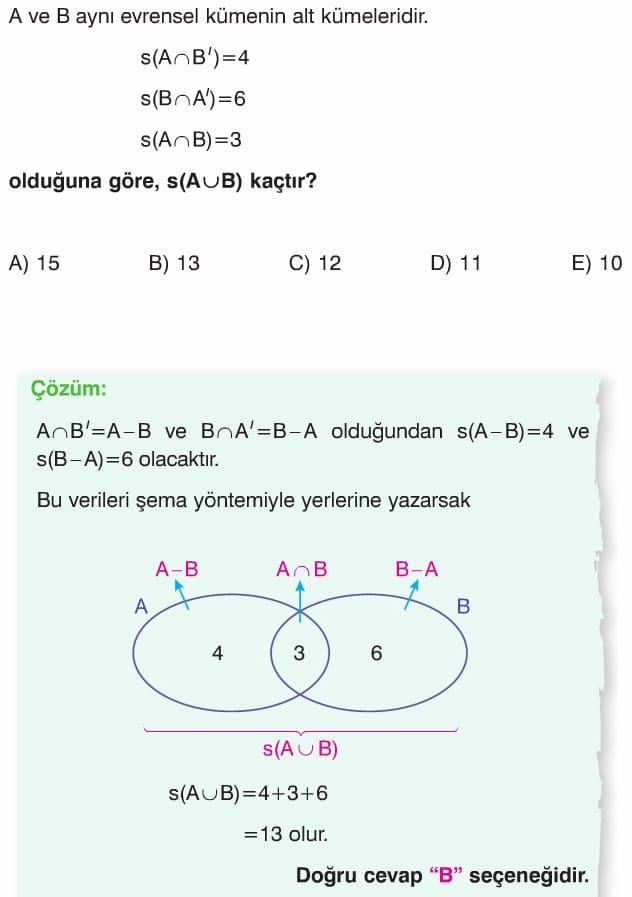
Örnek:
A = {1, 2, 3, 4}
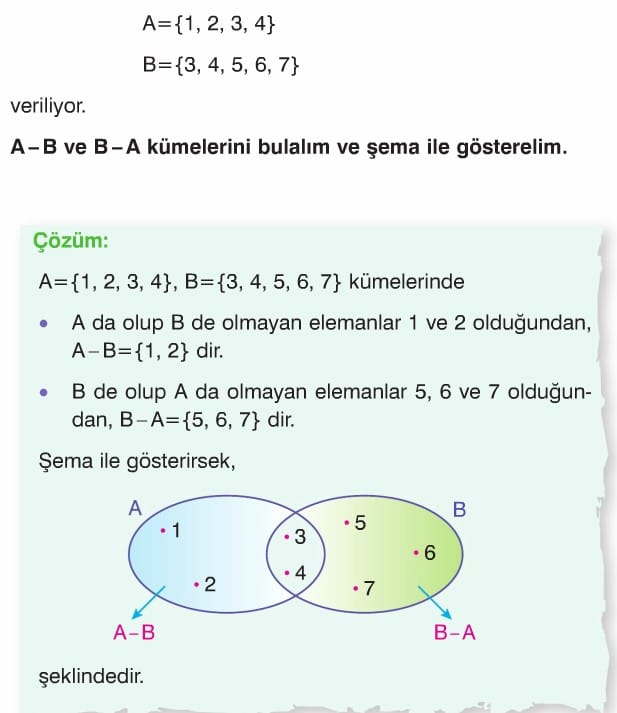
B = {3, 4, 5, 6, 7} kümeleri veriliyor.  A – B ve B – A kümelerini bulalım ve şema ile gösterelim.
Çözüm: A={1, 2, 3, 4}, B={3, 4, 5, 6, 7} kümelerinde A da olup B de olmayan elemanlar 1 ve 2 olduğundan, A – B = {1, 2} dir. B de olup A da olmayan elemanlar 5, 6 ve 7 olduğundan, B – A = {5, 6, 7} dir. Şema ile gösterin.

Örnek:
A = {a, b, c}
B = {1, 2, c, d}
C = {2, 3, a, b} kümeleri veriliyor. Buna göre, (A-  B) ∪ (C – A) kümesi aşağıdakilerden hangisidir?
A) {2, 3}    B) {1, 2, a}    C) {a, b, 3}
D) {a, b, 2, 3}    E) {b, c, 1}
Çözüm: A – B = {a, b} ve C – A = {2, 3} olacağından (A – B) ∪ (C – A) = {a, b} ∪ {2, 3} = {a, b, 2, 3} bulunur. Doğru cevap “D” seçeneğidir.

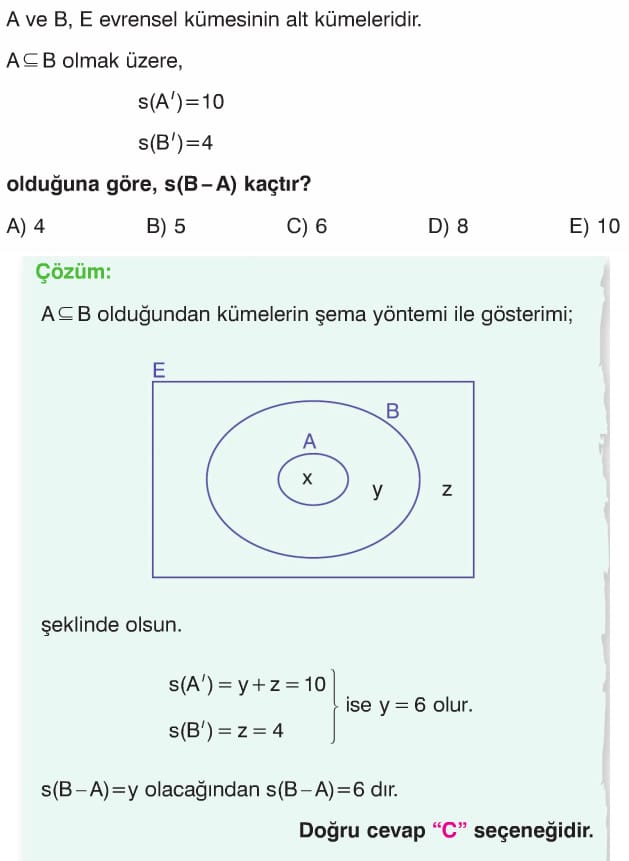
Örnek: A = {1, 2, 3} ve B = {6, 7, 8, 9} kümeleri veriliyor. A – B ve B – A kümelerini oluşturarak şema yöntemi ile gösterelim.
Çözüm: A={1, 2, 3} ve B={6, 7, 8, 9} veriliyor. A da olup B de olmayan elemanlar 1, 2 ve 3 tür. O halde A – B = {1, 2, 3} = A olur. B de olup A da olmayan elemanlar 6, 7, 8 ve 9 dur. O halde B – A = {6, 7, 8, 9} = B olur.

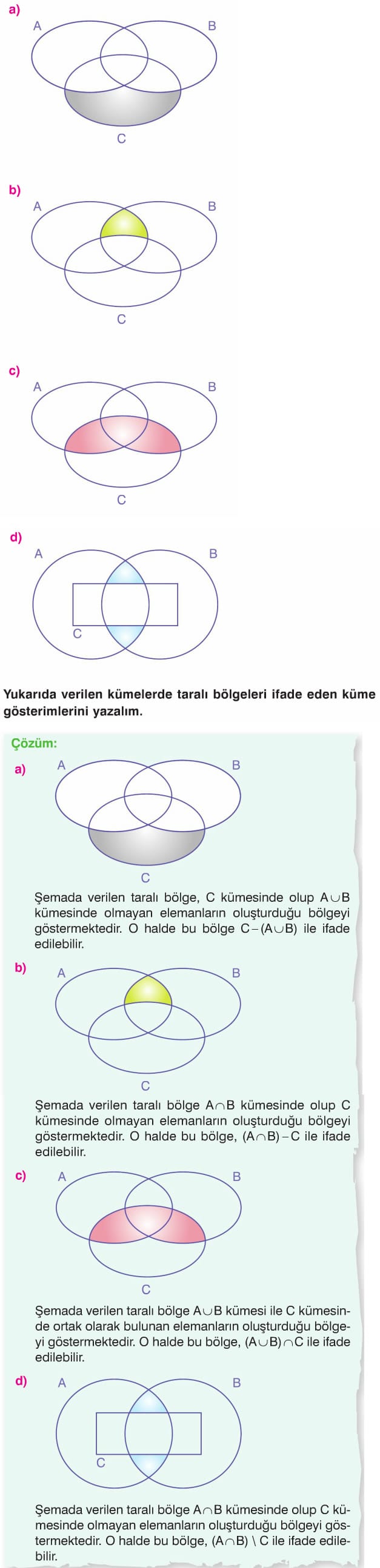
Örnek: A = {1, 2, 3, 4} kümesi E = {1, 2, 3, 4, 5, 6, 7} evrensel kümesinin alt kümesidir. Buna göre, A’ kümesini oluşturalım ve şema yöntemi ile gösterelim.
Çözüm: A = {1, 2, 3, 4} ve E = {1, 2, 3, 4, 5, 6, 7} olduğundan E kümesinde olup A kümesinde olmayan elemanlar 5, 6 ve 7 dir. O halde
A’= {5, 6, 7} olacaktır. Şema yöntemi ile gösterin.

Soru: E = {x | x alfabemizdeki harfler} evrensel kümesi,
A= {a, e, u, ü, p, ç, t, k) ve B = {a, b, c, ç, d, e, f, g, h}
kümeleri veriliyor. Buna göre, aşağıda verilen ifadelerin sonucu kaçtır?

Soru: A = {0, 3, 6, 9}
A’ ={1, 2, 4, 7}
B = {0, 2, 4, 6}
olduğuna göre B’ kümesi aşağıdakilerden hangisidir?
A) {5, 8) B) {1, 3, 5, 7, 9)
C) {2, 3, 6, 9) D) {1, 3, 7, 9)
E) {0, 2, 4, 6)

Soru: A alt küme E, B alt küme E ve A U B = E olmak üzere,
A = {2, 4, 6, 8}
B = {0, 3, 6, 9)}
kümeleri veriliyor.
Buna göre, s[(A n B) U B’] kaçtır?
A) 2 B) 3 C) 4 D) 5 E) 7