İki Kümenin Kartezyen Çarpımı ve Sıralı İkili 9. Sınıf
Sıralı İkili
Boş kümeden farklı A ve B kümeleri için A kümesinden bir a elemanı, B kümesinden bir b elemanı alınarak elde edilen ve (a, b) şeklinde gösterilen ifadeye sıralı ikili denir.
- Bu gösterimde a’ya birinci bileşen, b’ye ikinci bileşen denir.
Sıralı İkililerin Eşitliği
- (a, b) ve (c, d) birer sıralı ikili olsun.
- (a, b) = (c, d) ise a = c ve b = d
- a ≠ b ise (a, b) ≠ (b, a)

Sıralı İkili Soruları ve Çözümleri
Kartezyen Çarpım



Kartezyen Çarpım Grafiği


Kartezyen Çarpım Soruları ve Çözümleri
Kümeler Online Testler Tıklayın
Kartezyen Çarpım konu anlatımı özellikleri soruları örnekleri 9. sınıf İki Kümenin Kartezyen Çarpımı
Öncelikle bu konuda sıralı ikili kavramının bilinmesi gerekmektedir. Kısaca hatırlatırsak (a, b) ifadesine sıralı ikili demiştik. a birinci bileşen ve b ikinci bileşendir. (a, b) = (c, d) ise a = c ve b = c dir.
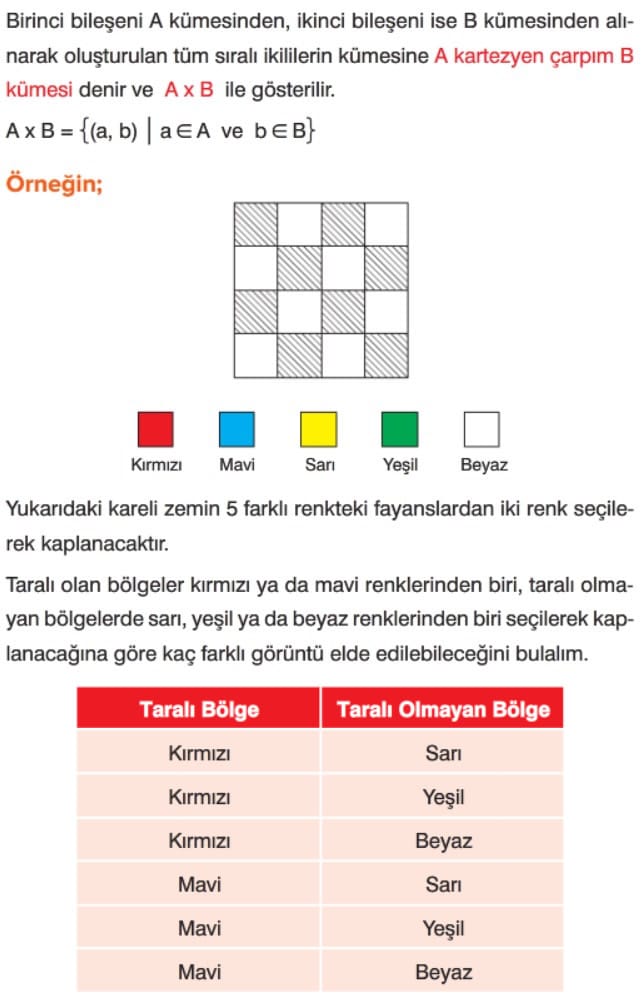
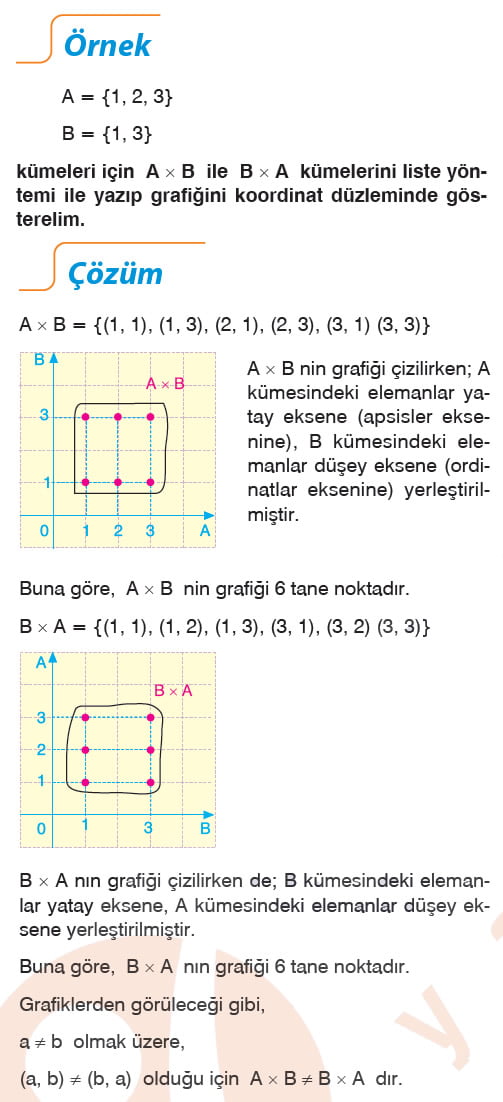
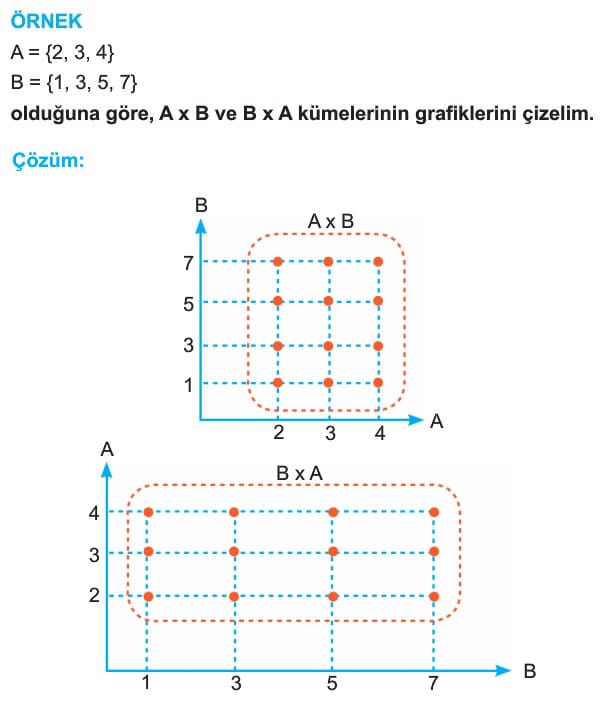
A ve B boş olmayan herhangi iki küme olsun. Birinci bileşeni A kümesinden, ikinci bileşeni B kümesinden alınarak oluşturulan bütün ikililerin kümesine Aile B'nin kartezyen çarpımı denir ve A x B şeklinde gösterilir. A x B = {(x, y) : x ∈ A ve y ∈ B}
Kartezyen çarpımın elemanları liste yöntemi, şema yöntemi ve grafik yöntemi ile gösterilir.
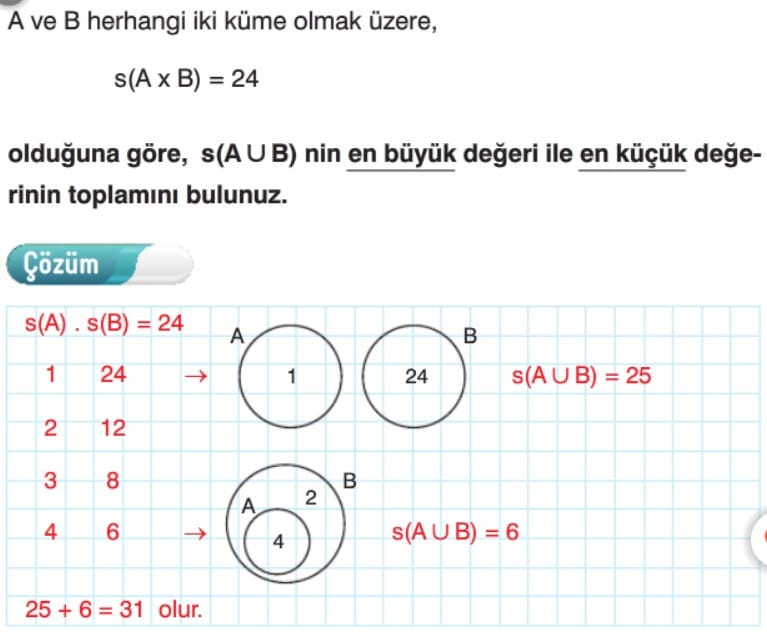
Kartezyen çarpımın eleman sayısı, s(A xB ) = s(A) x s(B) bağıntısı ile bulunur.
Kartezyen çarpımının özellikleri:
Kartezyen çarpımın birleşme özelliği vardır, değişme özelliği yoktur. Kartezyen çarpımın kesişim, birleşim ve fark işlemi üzerinde dağılma özelliği vardır.
A x A = A2
A x B ≠ B x A
AxBxC = (A x B) x C = A x (B x C)
s(A x B) = s(A) . s(B)
A x (B ∩ C) = (A x B) ∩ (A x C)
A x (B ∪ C) = (A x B) ∪ (A x C)
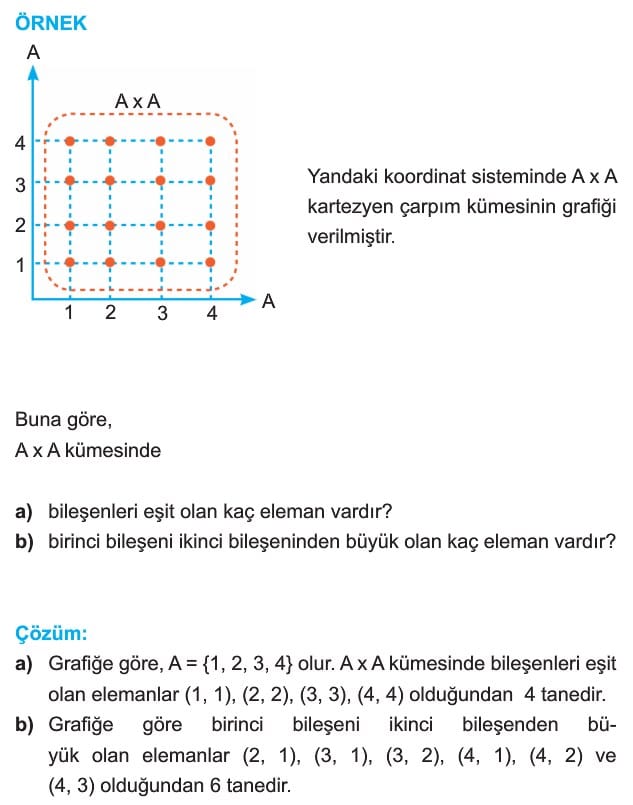
Örnek: Koordinat düzleminde A x A kartezyen çarpım kümesinin grafiği verilmiştir. Buna göre A x A kümesinde
a) Bileşenleri eşit olan kaç eleman vardır.
b) Birinci bileşeni ikinci bileşeninden büyük olan kaç eleman vardır?
Çözüm:
a) Grafiğe göre, A = {1, 2, 3, 4} olur. A x A kümesinde bileşenleri eşit olan elemanlar (1, 1), (2, 2), (3, 3), (4, 4) olduğundan 4 tanedir.
b) Grafiğe göre birinci bileşeni ikinci bileşenden büyük olan elemanlar (2, 1), (3, 1), (4, 1), (4, 2), (4, 3) olduğundan 6 tanedir.
Örnek: A = {1, 2, 3} ve B = {a, b} kümeleri veriliyor. Buna göre B x A kümesinin alt kümesinin kaç tanesinde (a, 1) elemanı bulunur?
Çözüm: s(A) = 3 ve s(B) = 2 olduğundan s(A x B) = 3 . 2 = 6 dır. B x A nın (a, 1) elemanı dışından 5 elemanı vardır. Bu elemanların oluşturduğu 2 üzeri 5 tane alt kümenin her birine (a, 1) eklenerek (a, 1) elemanının bulunduğu 2 üzeri 5 = 32 tane alt küme elde edilir.

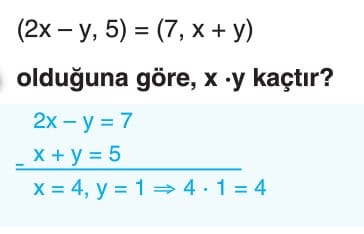






























Faydalı bence 👍👍……….