Üçgende Açı-Kenar İlişkisi

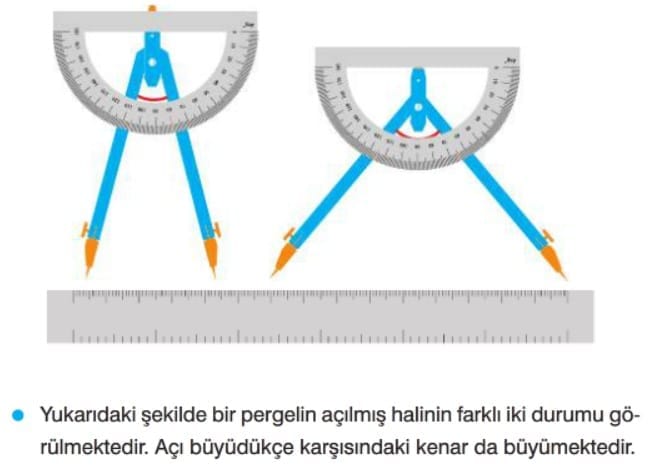
Çözümlü Sorular

Üçgen Eşitsizliği

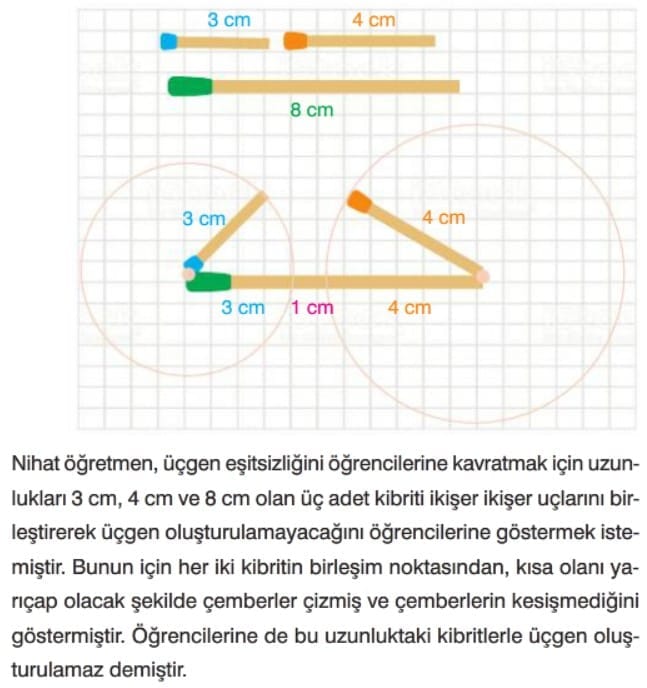
Çözümlü Sorular

Çözümlü Örnek Test Soruları: Üçgende Açı Kenar Bağıntıları ve Üçgen Eşitsizliği

Soru 1:

Bir üçgende kenar uzunlukları a = 7, b = 10 ve c olarak verilmiştir. Bu üçgenin oluşabilmesi için c kenarının alabileceği değer aralığı nedir?
A) 3 < c < 17
B) 4 < c < 18
C) 5 < c < 16
D) 2 < c < 15

Cevap: A
Çözüm: Üçgen eşitsizliğine göre, iki kenarın toplamı diğer kenardan büyük, farkı ise diğer kenardan küçük olmalıdır.
a + b > c → 7 + 10 > c → c < 17
b + c > a → 10 + c > 7 → c > 3
a + c > b → Bu eşitsizlik zaten c > 3 ile sağlanır.
Bu durumda 3 < c < 17.

---

Soru 2:

Bir üçgende kenar uzunlukları sırasıyla a = 6, b = 8, c = 10 olarak verilmiştir. Bu üçgenin en büyük açısı hangisidir?
A) A açısı
B) B açısı
C) C açısı
D) Hepsi eşit

Cevap: C
Çözüm: Üçgende en büyük açı her zaman en uzun kenarın karşısındadır. Burada en uzun kenar c = 10 olduğu için en büyük açı C açısıdır.

---

Soru 3:

Bir üçgende açı ölçüleri A açısı = 40 derece ve B açısı = 60 derece verilmiştir. Buna göre en uzun kenar hangisinin karşısındadır?
A) A açısının
B) B açısının
C) C açısının
D) Belirlenemez

Cevap: C
Çözüm: Üçgende en uzun kenar her zaman en büyük açının karşısındadır. Burada C açısı = 180 – 40 – 60 = 80 derece olduğu için en uzun kenar C açısının karşısındadır.

---

Soru 4:

Bir üçgende kenar uzunlukları x = 6, y = 8 ve z = 10 verilmiştir. Bu üçgenin dik üçgen olup olmadığını kontrol ediniz.
A) Dik üçgen
B) Dar açılı üçgen
C) Geniş açılı üçgen
D) Üçgen değildir

Cevap: A
Çözüm: Dik üçgen olup olmadığını anlamak için Pisagor teoremi uygulanır:
z² = x² + y²
10² = 6² + 8² → 100 = 36 + 64 → 100 = 100.
Bu nedenle üçgen bir dik üçgendir.

---

Soru 5:

Bir üçgende x + y = 12 ve x – y = 4 ise x ve y değerleri nelerdir?
A) x = 8, y = 4
B) x = 6, y = 6
C) x = 10, y = 2
D) x = 7, y = 5

Cevap: A
Çözüm: İki denklem toplanır:
(x + y) + (x – y) = 12 + 4 → 2x = 16 → x = 8
x yerine konulursa: x + y = 12 → 8 + y = 12 → y = 4.

---

Soru 6:

Bir üçgende kenar uzunlukları sırasıyla a = 5, b = 7 ve c = 10 olarak verilmiştir. Bu üçgenin dar açılı bir üçgen olup olmadığını kontrol ediniz.
A) Dar açılı üçgen
B) Dik üçgen
C) Geniş açılı üçgen
D) Üçgen değildir

Cevap: C
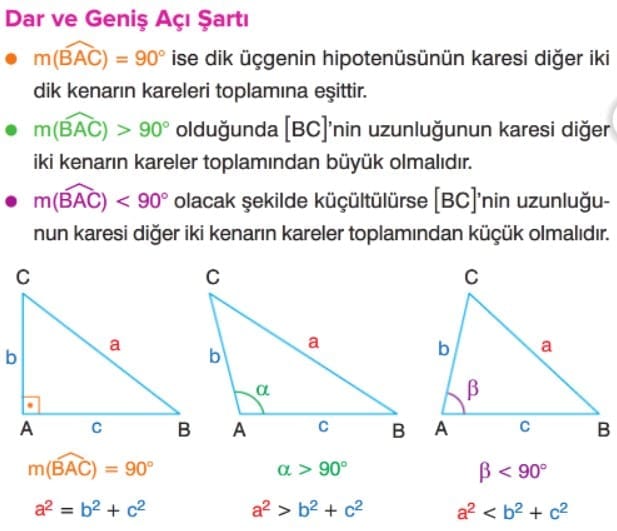
Çözüm: Üçgenin dar açılı olması için en büyük kenar c ile diğer kenarlar arasında c² < a² + b² şartı sağlanmalıdır.
c² = 10² = 100
a² + b² = 5² + 7² = 25 + 49 = 74
100 > 74 olduğundan, bu üçgen geniş açılıdır.

Üçgende Açı-Kenar İlişkisi:

1. İç Açı Toplamı: Bir üçgenin iç açıları toplamı her zaman 180 derecedir. Yani, A, B ve C iç açıları varsa, A + B + C = 180.

2. Dik Üçgen: Dik üçgende, dik açıya karşılık gelen kenarlar “kathet” olarak adlandırılır ve diğer iki kenar “hipotenüs” olarak adlandırılır. A^2 + B^2 = C^2 (Pisagor Teoremi) formülü geçerlidir.

3. Kenar Uzunlukları: Bir üçgenin herhangi bir kenarı, diğer iki kenarın toplamından küçüktür. Örneğin, üçgenin kenarları a, b ve c ise, a + b > c, a + c > b ve b + c > a.

Üçgen Eşitsizliği:

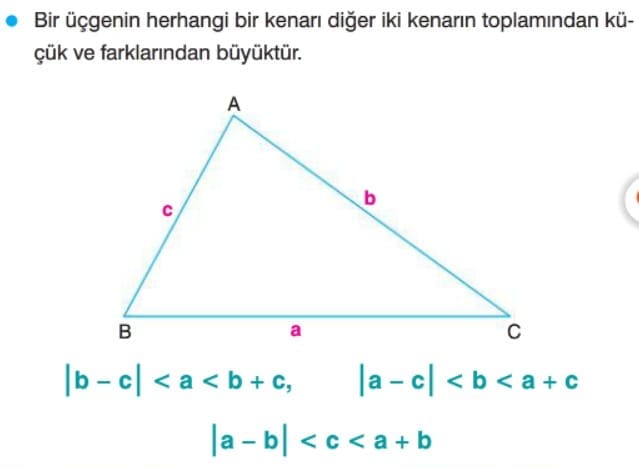
1. Bir Kenarın Uzunluğu: Herhangi bir üçgenin herhangi bir kenarı, diğer iki kenarın toplamından küçüktür.

2. İki Kenarın Uzunluğu: Herhangi bir üçgenin iki kenarı, diğer kenardan daha uzundur.

3. Üç Kenarın Uzunluğu: Üç kenarın uzunlukları ile yapılan herhangi bir açıma uyan bir üçgen, gerçek bir üçgendir.

Tarihçe:

Bu konular, antik Yunan matematikçileri tarafından ele alınmış ve geliştirilmiştir. Özellikle, Pisagor Teoremi’nin (M.Ö. 6. yüzyıl) bu alandaki önemli bir kilometre taşı olduğunu söyleyebiliriz. Yunan matematikçileri, üçgenlerin özelliklerini ve ilişkilerini sistemli bir şekilde inceleyerek bu alana önemli katkılarda bulunmuşlardır.

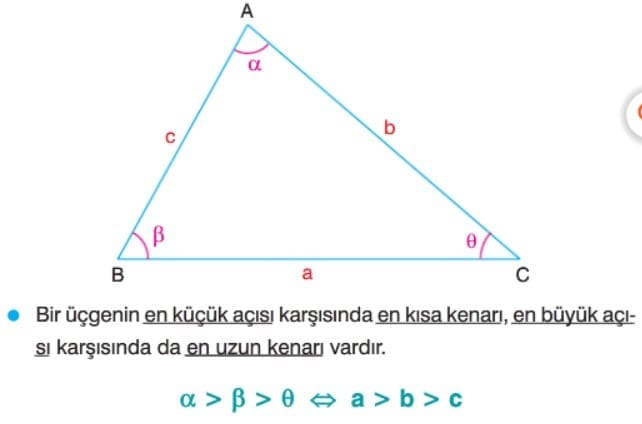
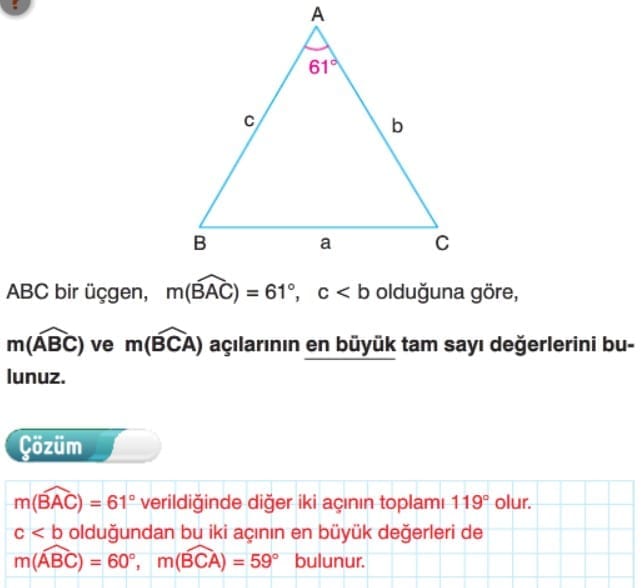
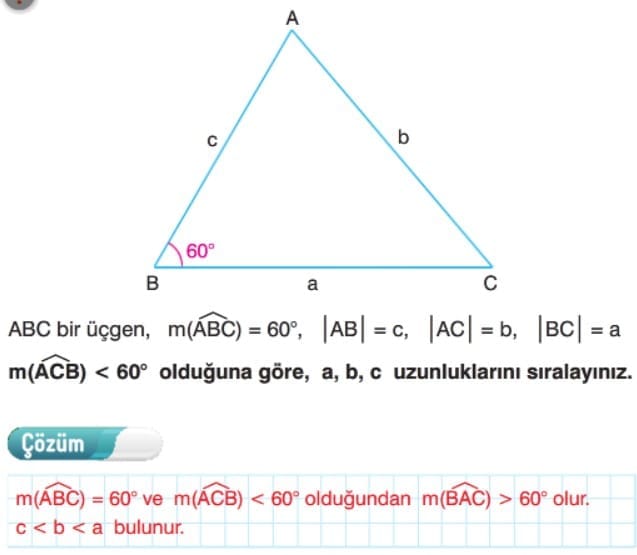
• Bir üçgende; büyük açı karşısında büyük kenar, küçük açı karşısında küçük kenar bulunur.
• Bir üçgende; büyük kenar karşısında büyük açı, küçük kenar karşısında küçük açı bulunur.
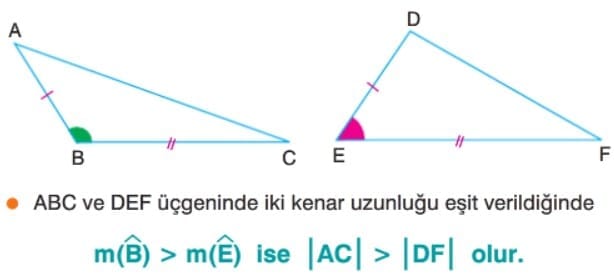
• Bir üçgende iki kenar eş değilse, ölçüsü daha büyük olan açının karşısında daha uzun kenar olur.

Bu kural bir üçgenin kenarları ile açıları arasında geçerlidir. Ancak bir üçgende; örneğin 20° lik bir açının karşısındaki kenar, başka bir üçgendeki 60° lik açının karşısındaki kenardan büyük olabilir. Çünkü bunlar farklı üçgenlerdir.

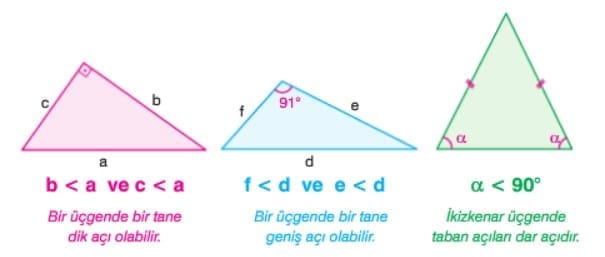
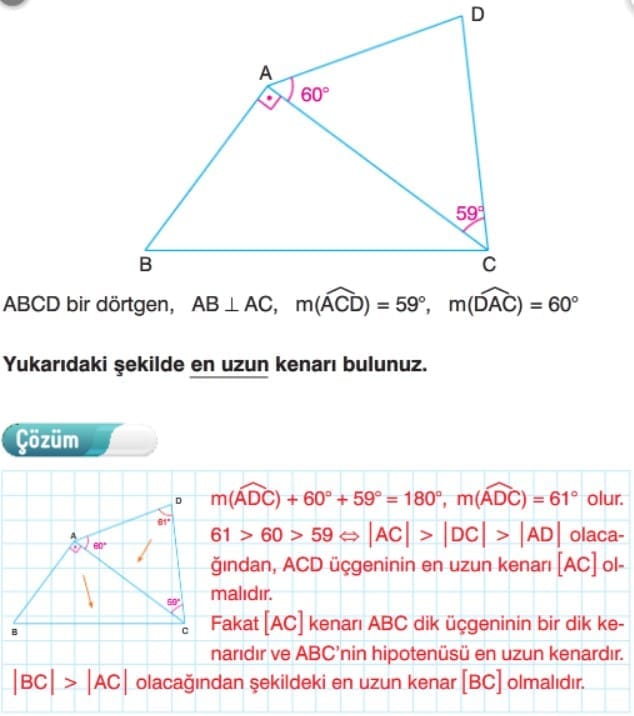
Bilgi: Bir dik üçgende en büyük kenar hipotenüstür. Geniş açılı bir üçgende en büyük kenar geniş açının karşısındaki kenardır.

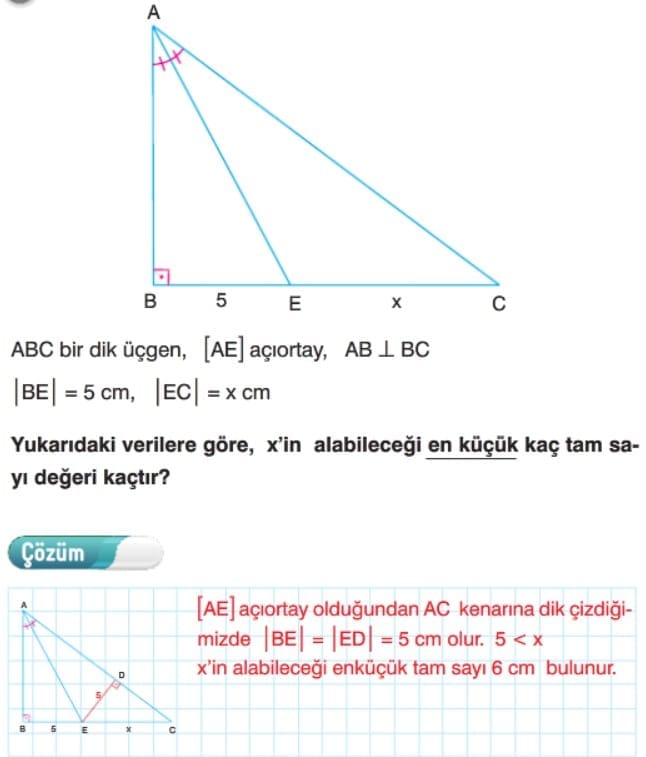
Bir üçgende herhangi bir kenarın uzunluğu diğer iki kenarın uzunlukları farkının mutlak değerinden büyük, toplamından küçüktür.
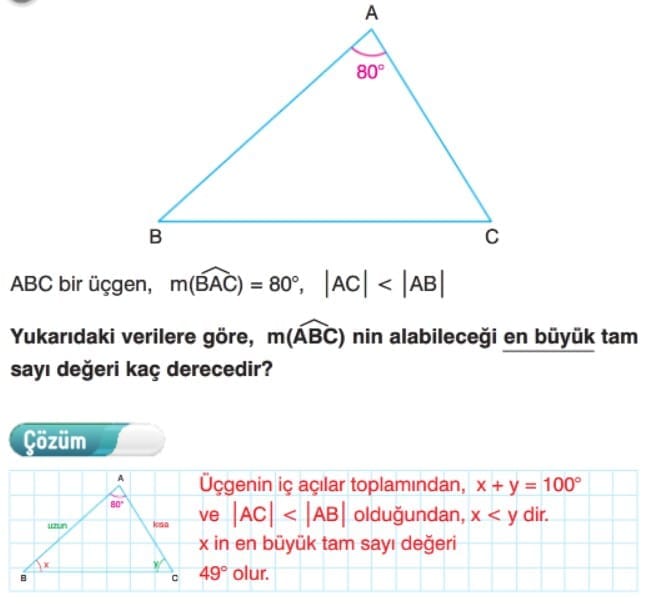
Çözüm: |AB| = |AC| olduğunu varsayalım. Tepe açısının ölçüsü 80° olan bir ikizkenar üçgenin taban açılarından her birinin ölçüsü 50° olur. Ancak |AB| < |AC| verildiğinden C açısı B açısından küçük olmalıdır. Bu durumda C açısı 50° den küçük olacaktır. Yani tam sayı olarak en fazla 49° olabilir.
Not: B açısının en küçük tam sayı değeri sorulsa idi 51° olacaktı.