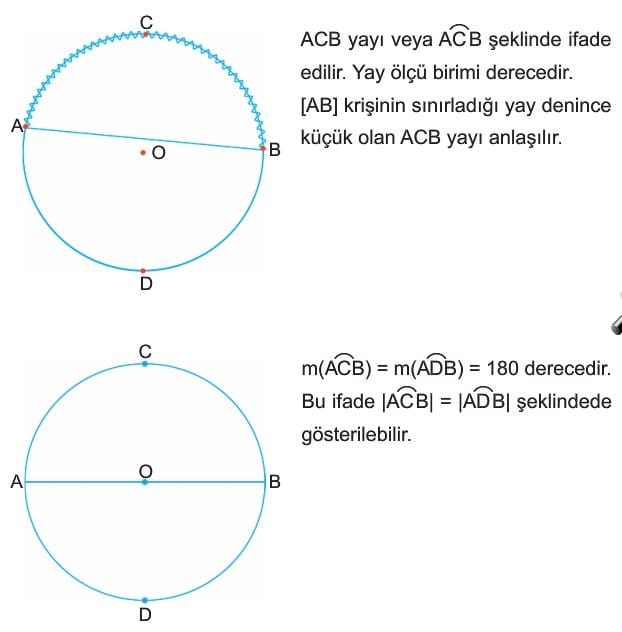
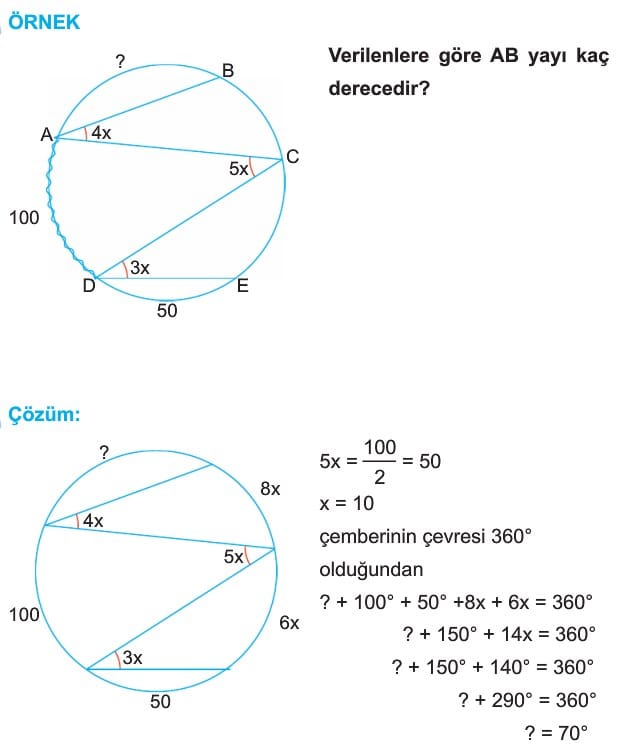
Çemberin iki noktası arasında kalan çember parçasına yay denir.

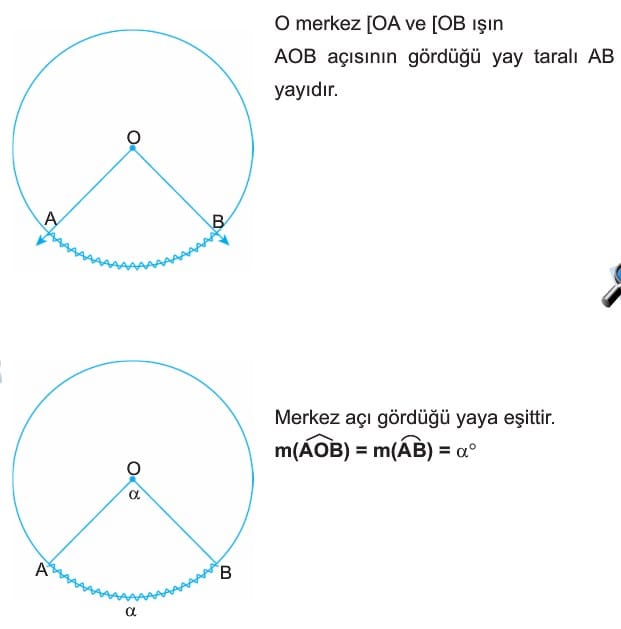
1. Merkez Açı

Köşesi çemberin merkezinde olan açıya merkez açı denir.

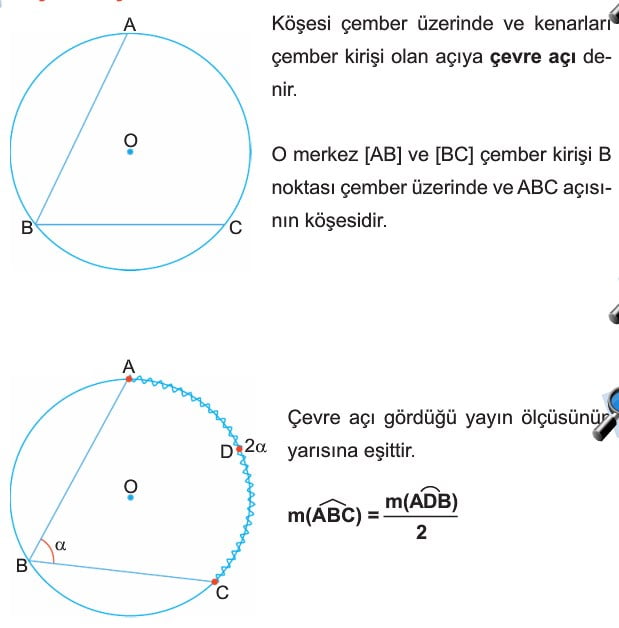
2. Çevre Açı

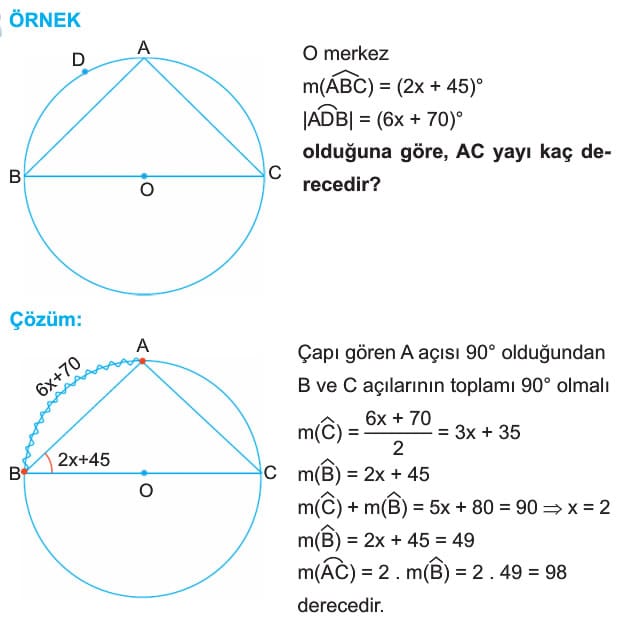
Bilgi: Çapı gören çevre açı 90 derecedir.

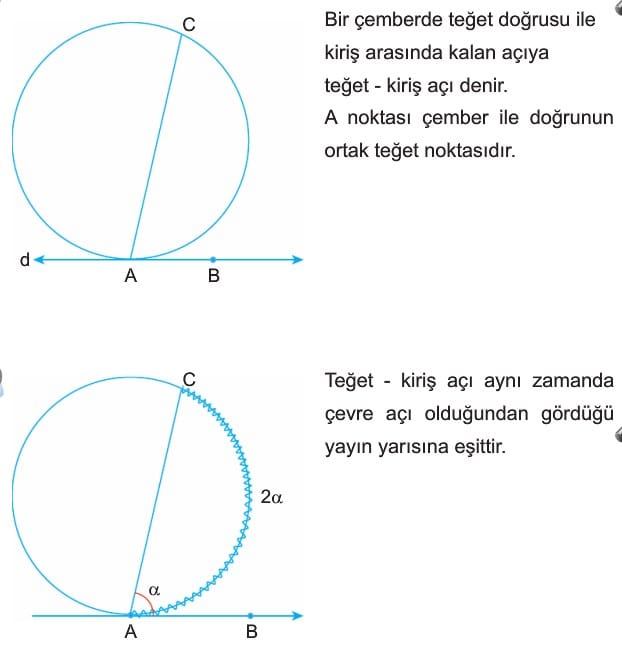
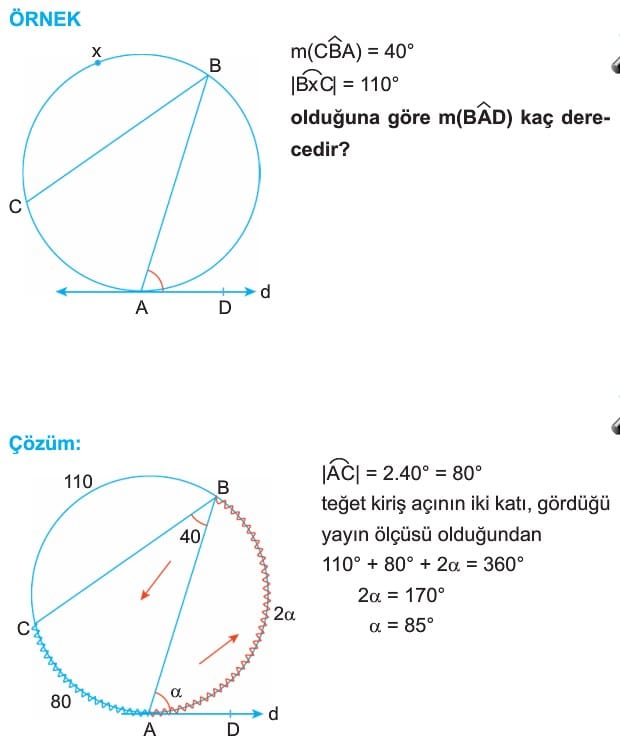
3. Teğet – Kiriş Açı

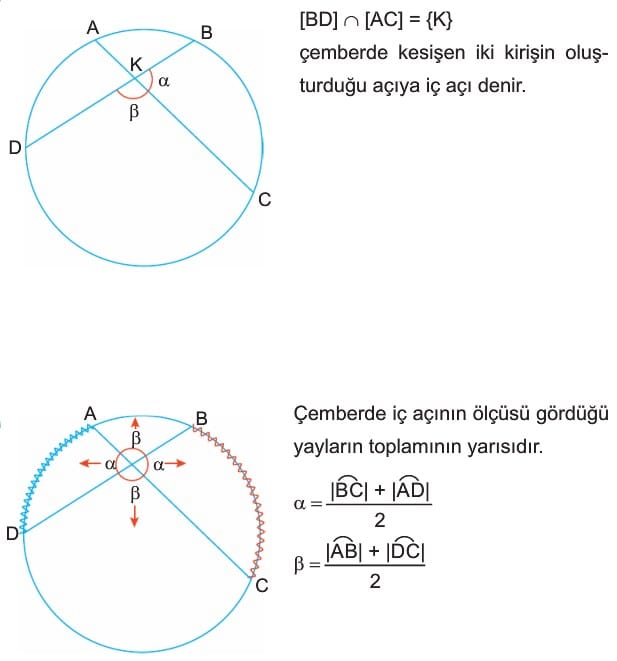
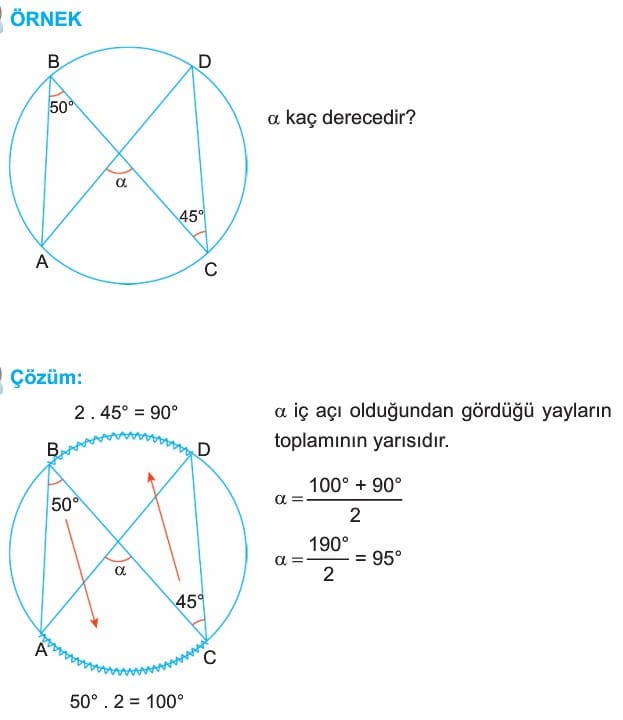
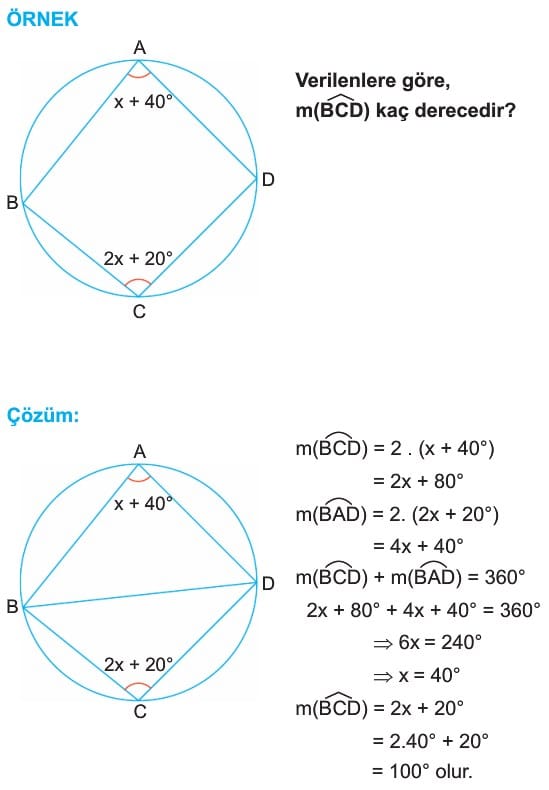
4. Çemberde İç Açı

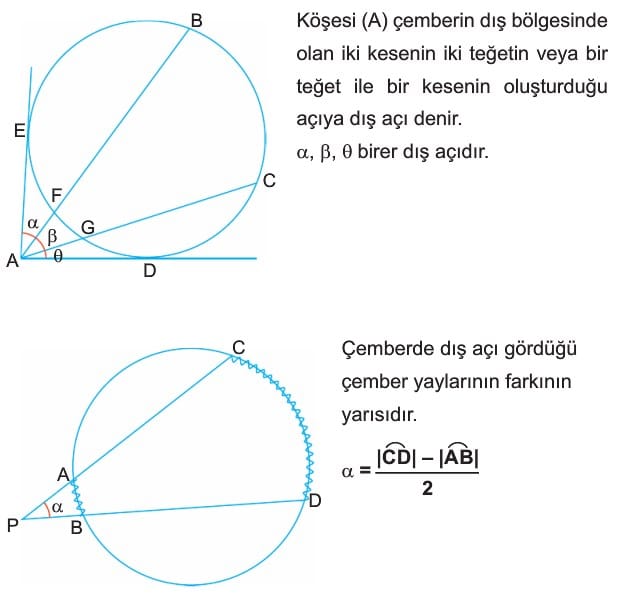
5. Çemberde Dış Açı

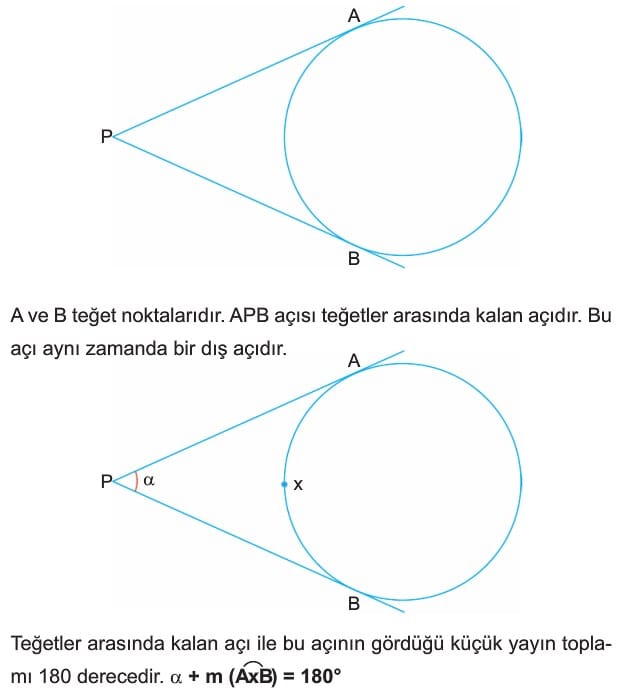
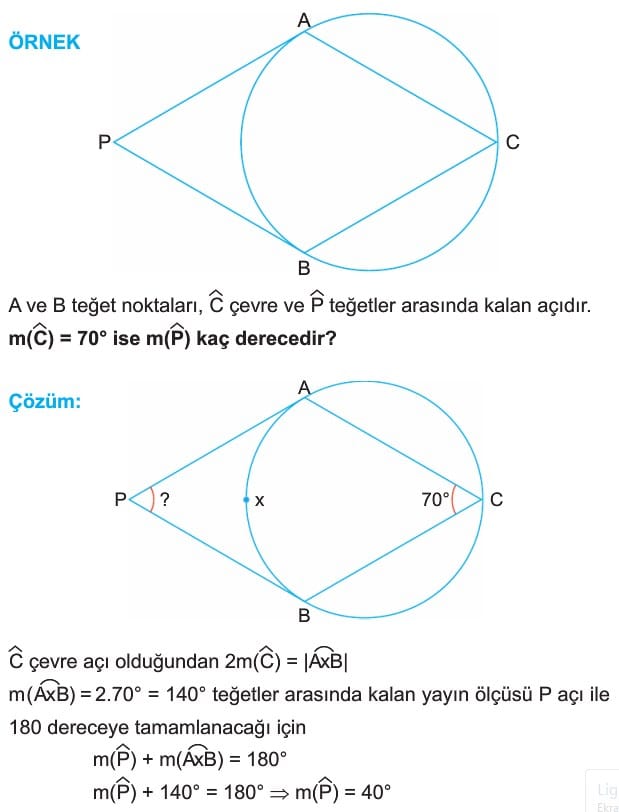
6. Teğetler Arasında Kalan Dış Açı

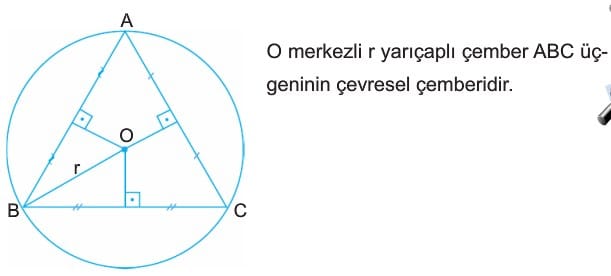
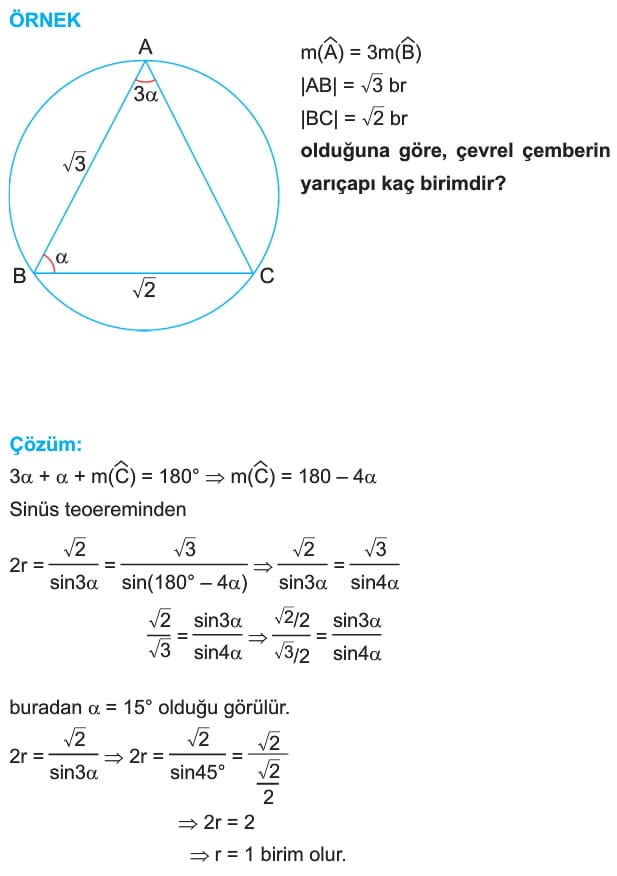
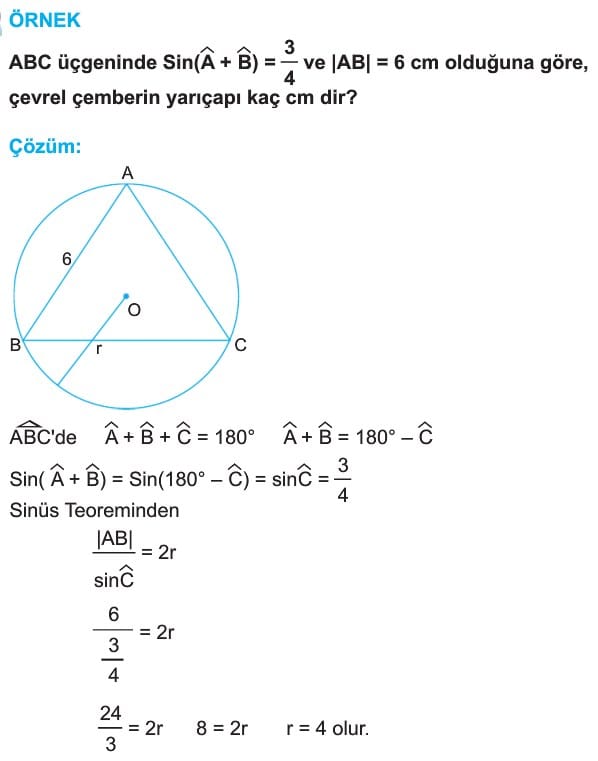
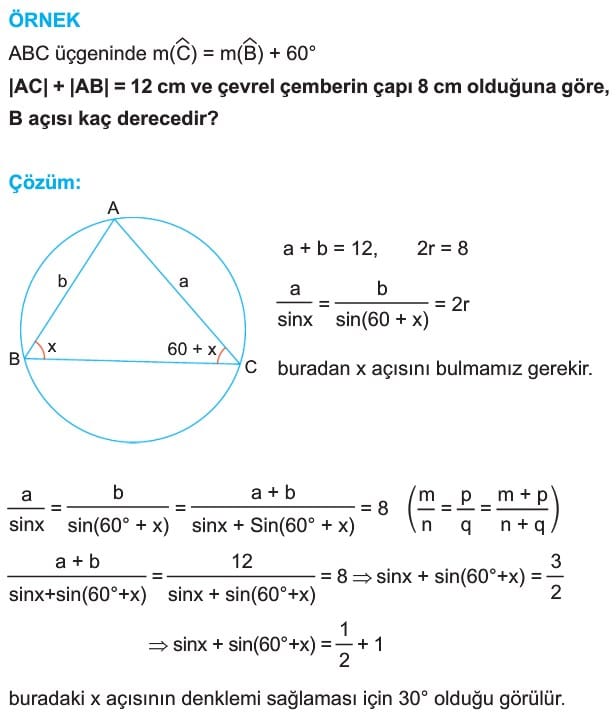
7. Bir Üçgenin Çevrel Çemberi

Bilgi: Tüm üçgenlerin bir çevrel çemberi mutlaka vardır. Üçgenin orta dikmelerinin kesim noktası çevrel çemberin merkezidir.

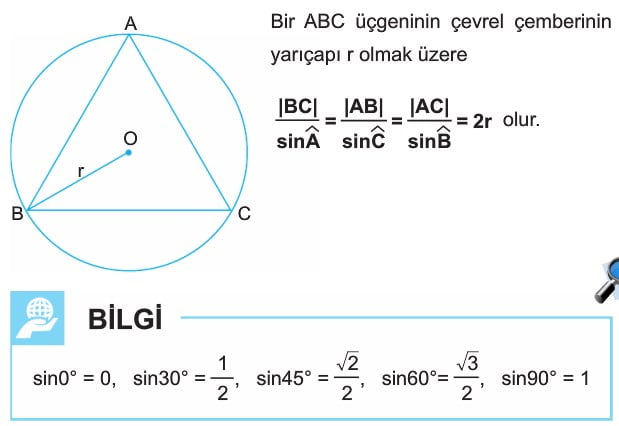
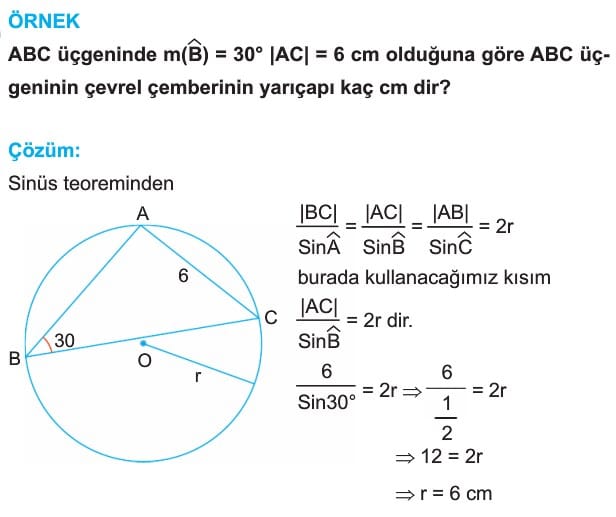
Sinüs Teoremi

Çemberde Açılar Soruları ve Çözümleri

Çözümlü Örnek Sorular: Çemberde Açılar

---

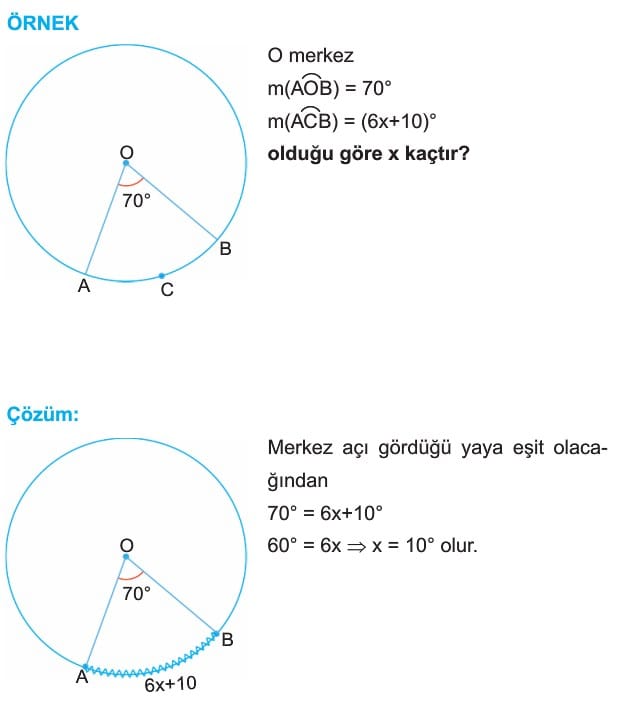
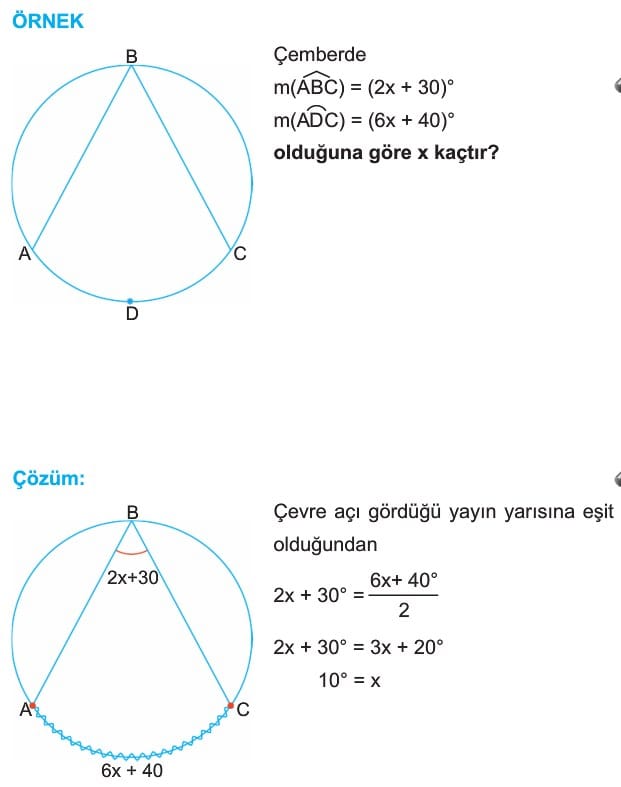
Çözümlü Örnek Soru 1: Çevre Açı ve Merkez Açı İlişkisi

Bir çemberde merkez açının ölçüsü 120° ise, aynı yayı gören çevre açının ölçüsü kaç derecedir?

Çözüm:

Çemberde çevre açı, gördüğü yayın yarısı kadardır. Merkez açı, çevre açının gördüğü yayın tamamını gördüğü için, çevre açı şu formülle bulunur:

Çevre açı = Merkez açı / 2

Çevre açı = 120° / 2 = 60°

Cevap: 60°

---

Çözümlü Örnek Soru 2: Çevre Açı ile Yay İlişkisi

Bir çemberde AB yayı 80° ve bu yayı gören çevre açının ölçüsü x°’dir. Buna göre, x kaçtır?

Çözüm:

Çevre açı, gördüğü yayın yarısıdır. Bu durumda:

Çevre açı (x) = Yay açısı / 2
x = 80° / 2 = 40°

Cevap: 40°

---

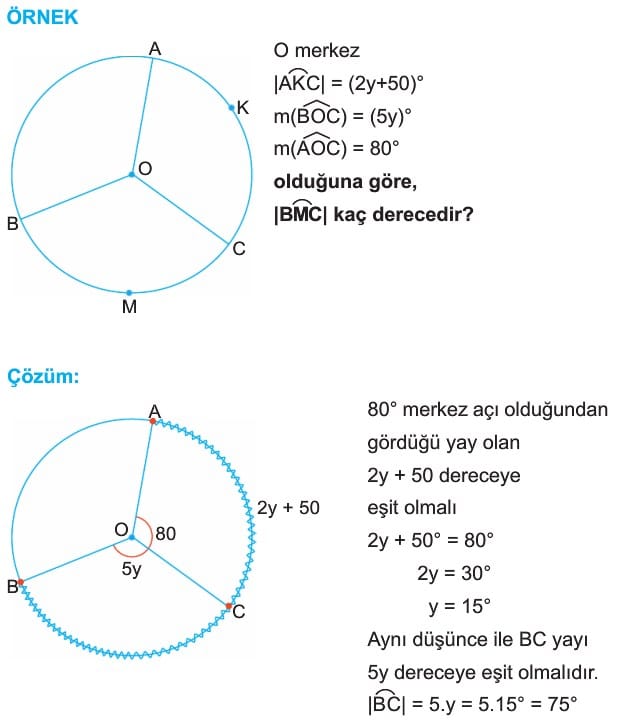
Çözümlü Örnek Soru 3: Merkez Açı ve Çevre Açı Hesaplaması

Bir çemberde AB yayı, merkezde 100° lik bir açı ile görülüyor. Bu yayı gören çevre açı kaç derecedir?

Çözüm:

Çevre açının gördüğü yay, merkez açının tamamını kapsadığı için formül yine aynı olacaktır:

Çevre açı = Merkez açı / 2
Çevre açı = 100° / 2 = 50°

Cevap: 50°

---

Çözümlü Örnek Soru 4: Yay Açısına Göre Çevre Açı Bulma

Bir çemberde bir yay 144°’lik açıyla görülüyor. Bu yayı gören çevre açının ölçüsü nedir?

Çözüm:

Çevre açı, yayı gören açının yarısıdır:

Çevre açı = Yay açısı / 2
Çevre açı = 144° / 2 = 72°

Cevap: 72°

---

Çözümlü Örnek Soru 5: Ters Açı Hesaplaması

Bir çemberde bir yayı gören iki çevre açıdan biri 70° ise, diğer çevre açının ölçüsü kaç derecedir?

Çözüm:

Aynı yayı gören çevre açılar birbirine eşittir. Bu durumda, diğer çevre açı da 70° olur.

Cevap: 70°

---

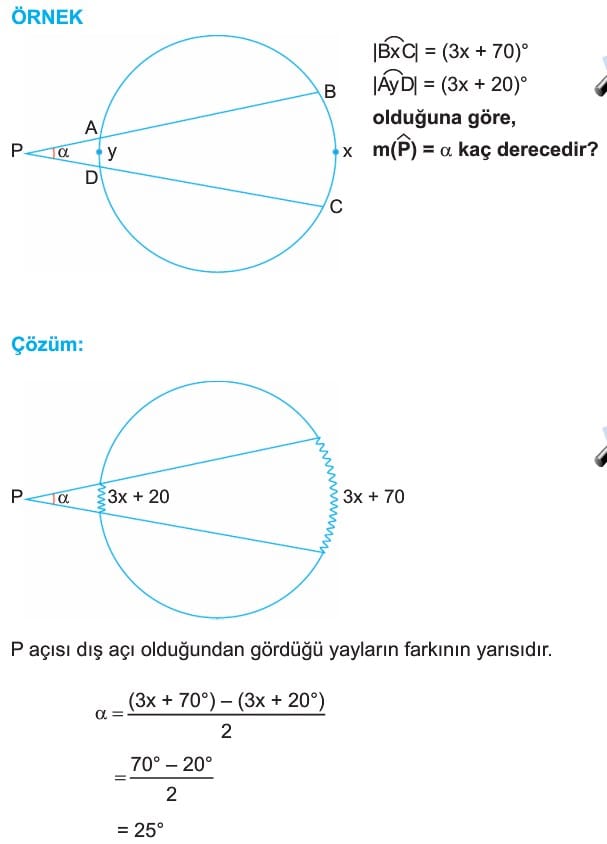
Çözümlü Örnek Soru 6: Dış Açı Hesaplaması

Bir çemberde iki kirişin oluşturduğu dış açının ölçüsü 40°’dir. Buna göre, bu açıya karşılık gelen iki yayın toplamı kaç derecedir?

Çözüm:

Dış açı, gördüğü iki yayın farkının yarısına eşittir. Eğer dış açı 40° ise, bu iki yay arasındaki fark şu şekildedir:

Dış açı = (Büyük yay – Küçük yay) / 2
40° = (Büyük yay – Küçük yay) / 2
Büyük yay – Küçük yay = 80°

Cevap: 80°

---

Çözümlü Örnek Soru 7: Çemberde İç Açı Hesaplaması

Bir çemberde iç açının ölçüsü 50° ve bu açının gördüğü iki yayı belirleyin. Yaylardan biri 120° ise diğer yayı bulun.

Çözüm:

Çemberde iç açı, gördüğü yayların toplamının yarısına eşittir:

İç açı = (Büyük yay + Küçük yay) / 2
50° = (120° + Küçük yay) / 2
100° = 120° + Küçük yay
Küçük yay = 100° – 120°
Küçük yay = 80°

Cevap: 80°

---

Çözümlü Örnek Soru 8: Dış Açı Hesaplaması

Bir çemberde bir dış açının ölçüsü 60° olup bu açıya karşılık gelen küçük yay 70° ise, büyük yayı bulun.

Çözüm:

Dış açı, iki yay arasındaki farkın yarısına eşittir:

Dış açı = (Büyük yay – Küçük yay) / 2
60° = (Büyük yay – 70°) / 2
120° = Büyük yay – 70°
Büyük yay = 120° + 70° = 190°

Cevap: 190°