Olasılık, matematikte günlük hayatımızda sıkça karşılaştığımız belirsiz olayların meydana gelme olasılığını ölçen bir bilim dalıdır. 10. sınıf matematik müfredatında yer alan basit olayların olasılıkları, öğrencilerin temel olasılık hesaplamalarını öğrenmeleri için başlangıç noktasıdır. Basit bir olay, yalnızca bir sonuçla ilişkili olan bir olaydır. Olasılıkla ilgili temel kavramları anlamak, gelecekteki daha karmaşık olasılık problemlerini çözmek için kritik bir beceridir. Bu giriş bölümünde, basit olayların olasılığına giriş yapacağız ve olayların nasıl hesaplandığını öğreneceğiz.

10. sınıf Basit Olayların Olasılıkları Testleri

10. sınıf Basit Olayların Olasılıkları Ders Notu

Olasılık hem günlük hayatta hem de değişik bilim dallarında çok sık kullanılır. Bugün olasılığın ekonomi, meteoroloji, temel bilimler, milli savunma, vb. birçok uygulama alanı vardır.

Deney: Bir olayın sonucunun ne olacağını görmek için yapılan işleme deney denir.
Çıktı: Deneyin sonucunda elde edilebilecek sonuçlara çıktı denir.
Örnek Uzay: Bir deneyde elde edilebilecek tüm çıktıların kümesine Örnek uzay denir ve E ile gösterilir.
Örnek Nokta: Ömek uzayın herhangi bir elemanına örnek nokta denir.

Bir madeni paranın bir kez atılması deneyinde, üste gelen yüz tur; (T) ya da yazı (Y) dır. Burada T ve Y örnek noktalardır.
E = {T, Y} örnek uzaydır.

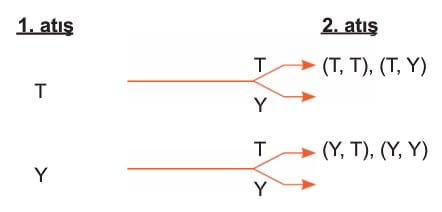
2 madeni para atıldığında örnek uzay, E = {(T, T), (T, Y), (Y, T), (Y, Y)} dır.

O halde, 1 madeni para atıldığında örnek uzay 2 elemanlıdır. 2 madeni para atıldığında örnek uzay 2² elemanlıdır.
…
…
n madeni para atıldığında örnek uzay 2ⁿ elemanlıdır.

Bir zarın bir kez atılması deneyinde; zarın üst yüzüne 1, 2, 3, 4, 5, 6 gelebileceği için örnek uzay,
E = (1, 2, 3, 4, 5, 6) dır ve s(E) = 6 dır.
Şimdi 2 zar atıldığında örnek uzayı bulalım.

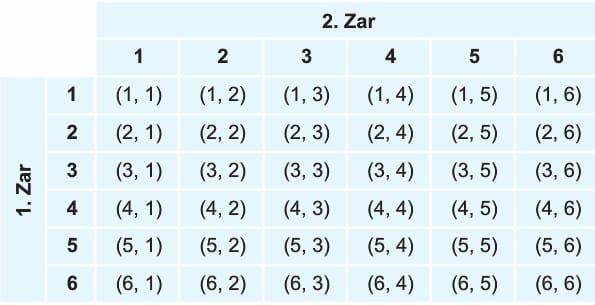
Zarların her birinin 6 yüzünde birbirinden farklı 6 sayı olduğundan örnek uzayın eleman sayısı 6 . 6 = 36 dır.
O halde,
1 zarın 1 kez atılması deneyinde örnek uzay 6 elemanlıdır.
1 zarın 2 kez atılması deneyinde örnek uzay 6² elemanlıdır.
…
…
1 zarın n kez atılması deneyinde örnek uzay 6ⁿ elemanlıdır.

Not: n tane zarın havaya atılması deneyinin örnek uzayı ile bir zarın arka arkaya n defa atılması deneyinin örnek uzayı birbirinin aynısıdır. Aynı şekilde n tane madeni paranın havaya atılması deneyinin örnek uzayı ile bir madeni paranın arka arkaya n defa havaya atılması deneyinin örnek uzayı birbirinin aynısıdır.

Eş Olası Durumlar

Eş Olası Olmayan Durumlar

Olay, imkânsız Olay, Kesin Olay

Olay: Örnek uzayın alt kümelerinden her birine olay denir.
imkânsız Olay: Boş kümeye imkânsız olay denir.
Kesin Olay: E örnek uzayının kendisine kesin olay denir.

Örneğin 2 zarın havaya atılması deneyinde,
a) Zarların üst yüzüne gelen sayıların toplamının 9 olması olayına A dersek;
A = {(3,6), (4, 5), (5, 4), (6, 3)} ve s(A) = 4 olur.
b) Zarların üst yüzüne gelen sayıların toplamının 14 olması imkânsız olaydır.
c) Üst yüze gelen sayıların toplamının 13 den küçük olma olayına kesin olay denir.

AYRIK OLAYLAR

Ayrık Olaylar: Bir örnek uzaya ait iki olayın kesişimi boş küme ise bu iki olaya ayrık olaylar denir.

Mesela, içerisinde 5 mavi, 8 beyaz bilye bulunan bir torbadan rastgele iki bilye çekiliyor. Bu bilyelerin ikisinin de beyaz olması olayıyla ikisi de mavi olması olayının kesişimi boş küme olduğundan bu olayla ayrıktır.

A ve B aynı örnek uzaya alt iki olay olsun. A ∩ B = Ø olduğundan bu olaylara ayrık olaylar denir.

NOT:

• A ve B olayları ayrık olaylar olup, her iki olayın aynı anda olma olasılığı P(A) . P(B) formülü ile bulunur.
• Ayrık iki olayın birleşiminin olasılığı P(A ∪ B) = P(A) + P(B) formülü ile bulunur.

Hilesiz iki zar atılıyor. Zarların üst yüzüne gelen sayıların toplamının 9 olması ile üst yüze gelen sayıların aynı olması ayrık olaydır.

Ayrık Olmayan Olaylar

Olasılık Fonksiyonu

Çözümlü Örnek Test Soruları: Basit Olayların Olasılıkları

Soru 1:

Bir zar atıldığında üst yüzeye gelen sayının çift olma olasılığı nedir?
A) 1/6
B) 1/3
C) 1/2
D) 2/3

Cevap: C
Çözüm: Bir zarın yüzeyinde 6 sayı bulunur: {1, 2, 3, 4, 5, 6}. Çift sayılar: {2, 4, 6} (3 adet).
Olasılık = İstenen durumların sayısı / Tüm durumların sayısı = 3 / 6 = 1/2.

Soru 2:

Bir torbada 5 kırmızı, 4 mavi ve 3 sarı top bulunmaktadır. Torbadan rastgele çekilen bir topun kırmızı olma olasılığı nedir?
A) 1/4
B) 1/3
C) 5/12
D) 7/12

Cevap: C
Çözüm: Toplam top sayısı = 5 + 4 + 3 = 12.
Kırmızı topların sayısı = 5.
Olasılık = 5 / 12.

Soru 3:

Bir torbada 8 top vardır: 3 kırmızı, 2 mavi ve 3 yeşil. Torbadan rastgele çekilen bir topun mavi olmama olasılığı nedir?
A) 1/4
B) 3/4
C) 2/3
D) 5/8

Cevap: B
Çözüm: Mavi topların sayısı = 2.
Mavi olmayan topların sayısı = 8 – 2 = 6.
Olasılık = 6 / 8 = 3 / 4.

Soru 4:

Bir zar iki kez atıldığında toplamlarının 7 olma olasılığı nedir?
A) 1/6
B) 5/36
C) 1/3
D) 1/12

Cevap: B
Çözüm: İki zarın toplamının 7 olması için şu durumlar geçerlidir:
(1,6), (2,5), (3,4), (4,3), (5,2), (6,1) → Toplam 6 durum.
Tüm durumların sayısı = 6 * 6 = 36.
Olasılık = 6 / 36 = 1 / 6.

Soru 5:

Bir deste karttan (52 kart) rastgele bir kart çekildiğinde çekilen kartın kupa olma olasılığı nedir?
A) 1/4
B) 1/2
C) 1/13
D) 3/4

Cevap: A
Çözüm: Bir destede 13 kupa kartı vardır.
Olasılık = 13 / 52 = 1 / 4.

Soru 6:

Bir kutuda 4 kırmızı, 3 mavi ve 5 yeşil bilye vardır. Rastgele seçilen bir bilyenin kırmızı ya da mavi olma olasılığı nedir?
A) 7/12
B) 1/2
C) 5/12
D) 3/4

Cevap: A
Çözüm: Toplam bilye sayısı = 4 + 3 + 5 = 12.
Kırmızı ya da mavi bilye sayısı = 4 + 3 = 7.
Olasılık = 7 / 12.