• Çember üzerinde farklı iki nokta arasında kalan çember parçasına yay denir.
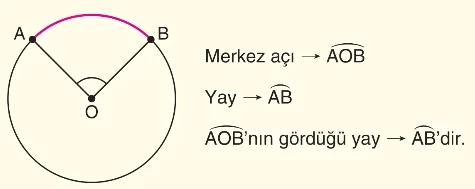
• Köşesi çemberin merkezinde olan açıya merkez açı ve bu açının iç bölgesinde (kolları arasında) kalan yaya da merkez açının gördüğü yay denir.
• Çemberi oluşturan toplam yayın ölçüsü 360 derecedir.

Merkez Açı – Yay Ölçüsü İlişkisi:

Merkez açının ölçüsü, gördüğü yayın ölçüsüne daima eşittir.

• Eğer bir merkez açının ölçüsü $\alpha$ ise, bu merkez açının gördüğü yayın ölçüsü de $\alpha$‘dır.
• Bir çemberin tamamının ölçüsü $360^\circ$‘dir.

Yayın Uzunluğu Hesaplama:

Yay uzunluğu, çemberin tamamının çevre uzunluğunun, yayın ölçüsüne (veya merkez açının ölçüsüne) orantılı bir parçasıdır.

Yayın uzunluğu ($L$), çemberin çevresinin $\frac{\text{Merkez Açı}}{360^\circ}$ katına eşittir.

Burada:

• $r$: Yarıçap
• $\pi$: Pi sayısı
• $\alpha$: Merkez açının ölçüsü (veya yayın ölçüsü)

Bu formül, sadece yayın ölçüsünü değil, aynı zamanda yayın uzunluğunu bulmak için kullanılır.

---

Soru 1:

$O$ merkezli bir çemberde, merkez açının ölçüsü $70^\circ$‘dir. Bu merkez açının gördüğü yayın ölçüsü kaç derecedir?

A) $35$

B) $70$

C) $140$

D) $290$

Çözüm 1:

Kural gereği, çemberde merkez açının ölçüsü, gördüğü yayın ölçüsüne eşittir.

Merkez açı $= 70^\circ$ ise, Gördüğü Yayın Ölçüsü $= 70^\circ$’dir.

Doğru Cevap: B

---

Soru 2:

Çapı $20 \text{ cm}$ olan bir çemberde $90^\circ$‘lik merkez açının gördüğü yayın uzunluğu kaç $\text{cm}$‘dir? ($\pi = 3$ alınız.)

A) $5$

B) $10$

C) $15$

D) $20$

Çözüm 2:

1. Çevre uzunluğunu bulma:

   Çap $D = 20 \text{ cm}$. $Ç = \pi \cdot D = 3 \times 20 = 60 \text{ cm}$.

2. Yayın uzunluğunu hesaplama:

    

   $$L = \text{Çevre} \times \frac{\text{Merkez Açı}}{360^\circ}$$

    

   $90^\circ$, $360^\circ$’nin $\frac{90}{360} = \frac{1}{4}$’üdür (Çeyrek çember).

    

   $$L = 60 \text{ cm} \times \frac{90}{360}$$
   $$L = 60 \times \frac{1}{4}$$
   $$L = 15 \text{ cm}$$

Doğru Cevap: C

---

Soru 3:

$O$ merkezli bir çemberde, $\text{AOB}$ merkez açısının gördüğü $\text{AB}$ yayının ölçüsü $115^\circ$‘dir. $\text{AOB}$ açısının ölçüsü kaç derecedir?

A) $115$

B) $230$

C) $245$

D) $360$

Çözüm 3:

Merkez açının ölçüsü, gördüğü yayın ölçüsüne eşittir.

Yayın Ölçüsü $= 115^\circ$ ise, Merkez Açı ($\text{AOB}$) $= 115^\circ$’dir.

Doğru Cevap: A

---

Soru 4:

Yarıçapı $6 \text{ cm}$ olan bir çemberin çevre uzunluğu $36 \text{ cm}$‘dir. $60^\circ$‘lik merkez açının gördüğü yayın uzunluğu kaç $\text{cm}$‘dir?

A) $3$

B) $6$

C) $12$

D) $18$

Çözüm 4:

Verilen çevre uzunluğunu kullanacağız: $Ç = 36 \text{ cm}$.

 

 

$60^\circ$, $360^\circ$’nin $\frac{60}{360} = \frac{1}{6}$’sıdır.

 

Doğru Cevap: B

---

Soru 5:

$O$ merkezli bir çemberde $36^\circ$‘lik merkez açının gördüğü yay, çemberin çevresinin kaçta kaçıdır?

A) $\frac{1}{10}$

B) $\frac{1}{8}$

C) $\frac{1}{6}$

D) $\frac{1}{5}$

Çözüm 5:

Yayın çemberin çevresine oranı, merkez açının $360^\circ$’ye oranına eşittir.

 

 

Sadeleştirme yapılırsa:

 

Doğru Cevap: A

---

Soru 6:

Yarıçapı $12 \text{ cm}$ olan bir çemberde, $\text{AB}$ yayının uzunluğu $6 \pi \text{ cm}$‘dir. Bu yayı gören merkez açının ölçüsü kaç derecedir? ($\pi$ yerine sayısal değer kullanmayınız.)

A) $60$

B) $90$

C) $120$

D) $150$

Çözüm 6:

1. Çevreyi $\pi$ cinsinden hesaplama:

   $Ç = 2 \cdot \pi \cdot r = 2 \cdot \pi \cdot 12 = 24 \pi \text{ cm}$

2. Yayın uzunluğu formülünü kullanma:

    

   $$L = \text{Çevre} \times \frac{\alpha}{360^\circ}$$
   $$6 \pi = 24 \pi \times \frac{\alpha}{360^\circ}$$
3. $\alpha$’yı bulma:

   Denklemin her iki tarafındaki $\pi$’ler sadeleşir:

    

   $$6 = 24 \times \frac{\alpha}{360}$$
   $$\frac{6}{24} = \frac{\alpha}{360}$$
   $$\frac{1}{4} = \frac{\alpha}{360}$$

    

   İçler dışlar çarpımı yapılır:

    

   $$4 \times \alpha = 360$$
   $$\alpha = 360 \div 4 = 90^\circ$$

Doğru Cevap: B

---

Soru 7:

Bir çemberdeki merkez açıların ölçüleri $1:2:3:4$ oranındadır. En büyük merkez açının gördüğü yayın ölçüsü kaç derecedir?

A) $72$

B) $108$

C) $144$

D) $180$

Çözüm 7:

1. Oran toplamını bulma:

   Oranlar $1k, 2k, 3k, 4k$ olsun.

   Toplam oran: $1k + 2k + 3k + 4k = 10k$

2. $k$ değerini bulma:

   Çemberdeki merkez açıların toplamı $360^\circ$’dir.

    

   $$10k = 360^\circ$$
   $$k = 36^\circ$$
3. En büyük açıyı bulma:

   En büyük merkez açı $4k$’dır.

    

   $$\text{En Büyük Açı} = 4k = 4 \times 36^\circ = 144^\circ$$
4. Yayın ölçüsünü bulma:

   Merkez açının ölçüsü, gördüğü yayın ölçüsüne eşittir.

    

   $$\text{Yayın Ölçüsü} = 144^\circ$$

Doğru Cevap: C