Açı Çeşitleri 9. Sınıf
Dar Açı
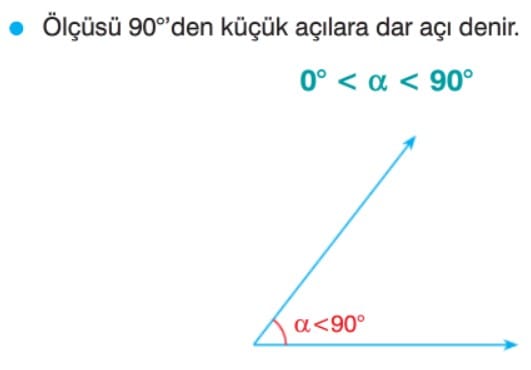
Dik Açı
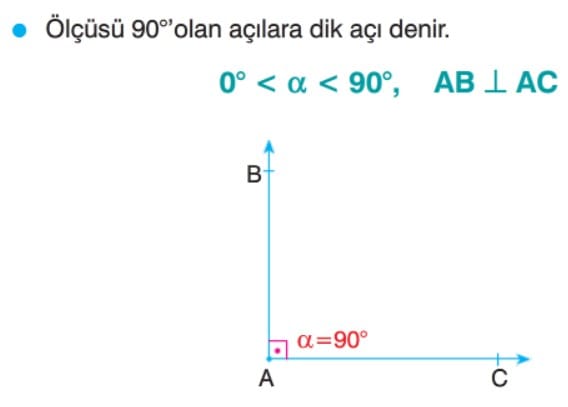
Geniş Açı
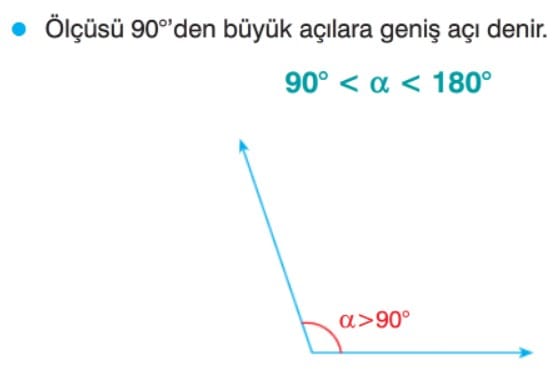
Doğru Açı
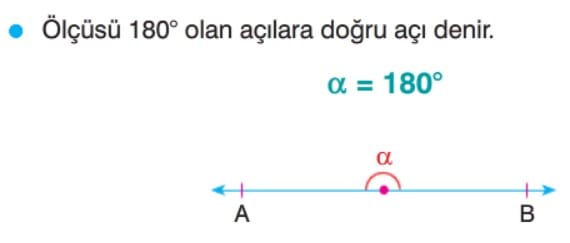
Tam Açı

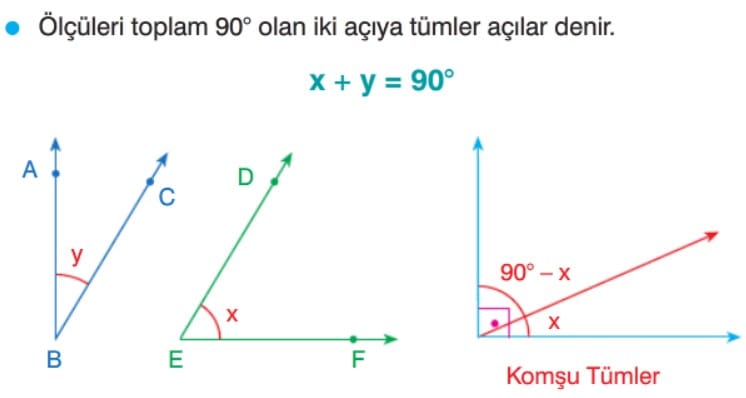
Tümler Açı
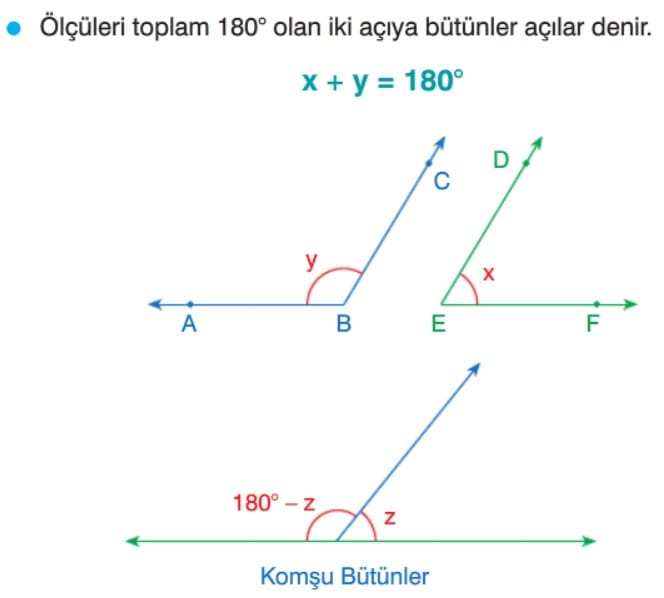
Bütünler Açı
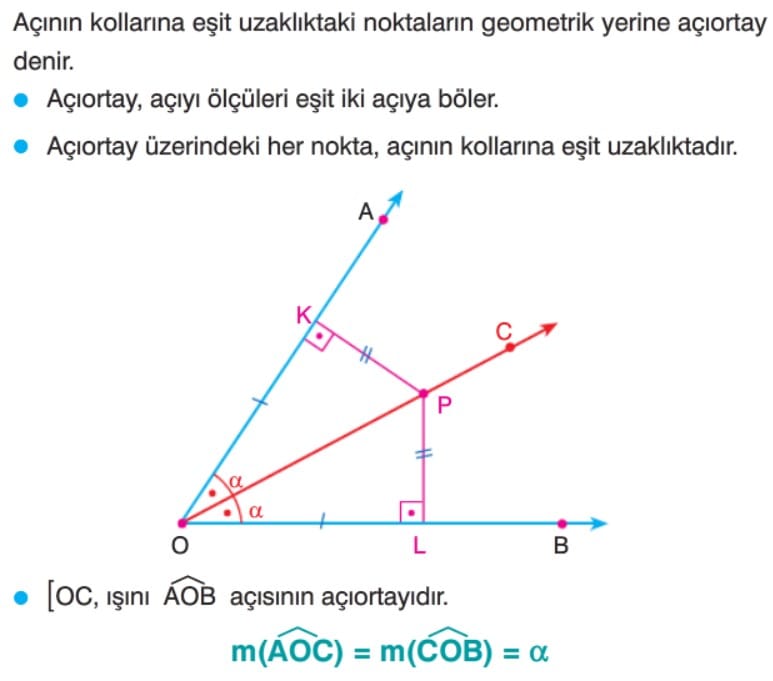
Açıortay
Çözümlü Sorular
Paralel İki Doğrunun Bir Kesenle Yaptığı Açılar
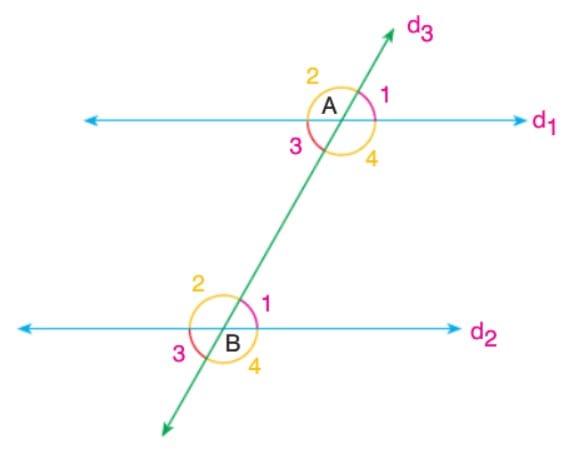
Yöndeş Açılar

İç Ters Açılar

Dış Ters Açılar

Karşıt Durumlu Açılar

Bilgi:
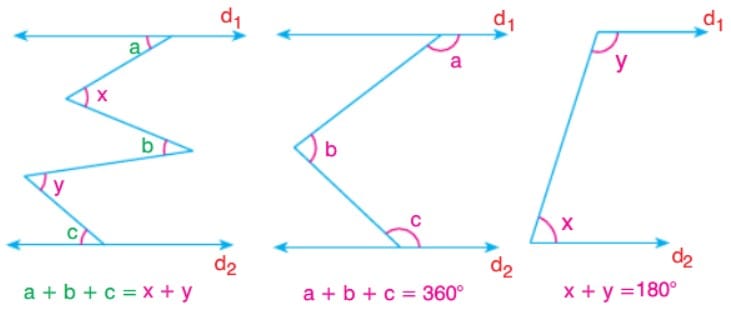
Çözümlü Sorular
Açı Çeşitleri konu anlatımı soruları çözümleri 9. Sınıf Matematik
Soru: CD ışını ile OA ışını paralel, OB ışını OE ışınına dik, BCD açısı 4x derece olduğuna göre EOA = x açısı kaç derecedir?
Çözüm: CD ve OA ışınları paralel olduklarından dolayı BCD ve BOA açıları yöndeş açılar olup ölçüleri eşittir. Buna göre 4x = 90 + x ise x = 30 derece olarak bulunur.
Soru: AB ve CD doğruları birbirine paralel, EH ve FH doğru parçaları birbirine dik, EG doğru parçası ile FK ışını birer açıortay olduğuna göre, KGE = x açısının ölçüsünü bulunuz.
Çözüm: EG doğru parçası ile FK ışını açıortay olduklarından dolayı AEG ve GEH açıları eşit ve a olsun, CFK ve KFH açıları eşit ve b olsun. Şekilde AB ve CD doğruları paralel olduklarından dolayı BEH ve HFD açıların ölçüleri toplamı EHF açısının ölçüsüne eşittir. Buradan c + d = 90 derece bulunur. AEB ve CFD açıları doğru açılar olduklarından ölçüleri 180 derecedir. 2a + c + 2b = 360 derece ve 2a + 2b + (c + d) = 360 derece, 2 (a + b) + 90 derece = 360 derece, a + b = 135 derece olur. a + b 135 derece olduğundan x = 180 - 135 den 45 derece olarak bulunur.
Açılar, iki ışın veya kenar arasındaki yönlendirilmiş uzay bölgesidir. Açılar, derece veya radyan gibi ölçü birimleriyle ifade edilirler. Açılar, genellikle konik kesitler, trigonometri, geometri ve diğer matematik konularında önemli bir rol oynar.
Tümler ve Bütünler Açılar Problemleri:
- Gerçek hayat problemlerinde tümler ve bütünler açılar kullanılarak açı ölçüleri hesaplanabilir.
- Örneğin, bir dik üçgenin bir açısı verildiğinde, tümler açılar kullanılarak diğer açıların ölçüsü bulunabilir.
Geometrik Şekillerde Tümler ve Bütünler Açılar:
- Kare, dikdörtgen veya paralel kenar gibi geometrik şekillerde tümler ve bütünler açılar sıkça karşımıza çıkar.
- Örneğin, dikdörtgenin karşılıklı köşegenleri birbirine bütünler açılardır.
Bu kavramlar, antik Yunan matematikçileri tarafından ele alınmıştır. Özellikle Euclid'in "Öklidyen Geometri" adlı eseri, bu tür konseptleri detaylı bir şekilde açıklar. Açılarla ilgili temel kavramlar ve özellikler, antik Yunan matematiğinin yanı sıra Ortaçağ ve Rönesans dönemlerinde de geliştirilmiştir. Geometrinin temel prensipleri olarak, tümler ve bütünler açılar günümüzde de matematik eğitiminde önemli bir yer tutmaktadır.