Geometri, çevremizdeki şekilleri ve bu şekillerin özelliklerini inceleyen bir matematik dalıdır. Geometrik şekiller, matematiğin temel konularından biridir ve hayatımızın birçok alanında karşımıza çıkar. Çizgiler, açıların ölçülmesi, çokgenler ve daireler gibi şekillerin doğru tanımlanması ve bu şekillerin özelliklerini bilmek, öğrencilerin matematiksel düşünme becerilerini geliştirmeleri için önemlidir. Bu yazıda, temel geometrik şekilleri ve bu şekillerin özelliklerini inceleyeceğiz.

5. Sınıf Temel Geometrik Şekiller ve Özellikleri Testleri

5. Sınıf Temel Geometrik Şekiller ve Özellikleri Ders Notu (2024 – 2025 Yeni Müfredat)

Nokta

Kalemin kâğıda dokundurulmasıyla oluşan iz bir nokta modelidir. Noktanın eni, boyu ve derinliği yoktur. Noktalar büyük harf ile gösterilir.

Doğru Parçası

Düz bir çizgi oluşturmak için kullanılan ve üzerinde birimlerin olmadığı cetvele ölçüsüz cetvel (çizgeç) denir.

Ölçüsüz Cetvel

Örnek: Ölçüsüz cetvel kullanarak iki nokta arası düz ve hiç boşluk kalmayacak şekilde noktalarla dolduralım.

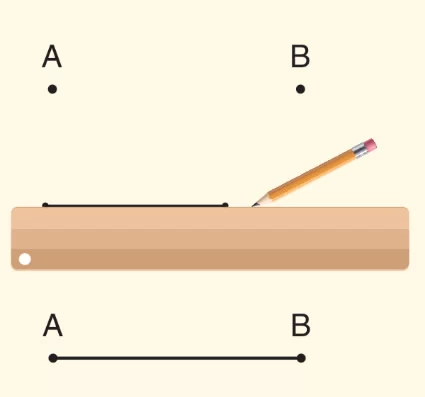
• İki nokta arasındaki tüm noktaların oluşturduğu düz çizgiye doğru parçası denir.

Yukarıdaki doğru parçası CD veya DC doğru parçası diye okunur.
Sembolle; [CD] veya [DC] şeklinde gösterilir.

Işın:

• Bir noktadan başlayarak belirli bir yönde sınırsız uzayan noktalardan oluşan düz çizgiye ışın denir. Işınlar, başlangıç noktasına ve üzerindeki bir noktaya verilen harfler ile isimlendirilir. Başlangıç noktası K olan ve L noktasından geçen ışın KL ışını şeklinde okunur ve aşağıdaki gibi gösterilir;

Doğru:

• Her iki yönden de sınırsız olarak devam eden noktalardan oluşan düz çizgiye doğru denir. Doğrular, üzerinde bulunan farklı iki nokta ile isimlendirilerek sembolle gösterilir. Ayrıca doğrular aşağıda görüldüğü gibi küçük harfle de adlandırılabilir.

Doğru Parçasının Uzunluğu:

• Doğru parçası iki nokta ile adlandırılır. Örneğin, A ve B noktaları arasında bir doğru parçası varsa, bu doğru parçası [AB] veya [BA] olarak gösterilir.
• Eğer bu doğru parçasının uzunluğunu ifade etmek istiyorsak, uzunluğu şu şekilde yazarız: ∣AB∣ = uzunluk

Burada, |AB| sembolü, A ve B noktaları arasındaki doğru parçasının uzunluğunu ifade eder. Cetvel ile ölçüldüğünde, örneğin 8 cm ise, şu şekilde gösterilir: ∣AB∣=8 cm

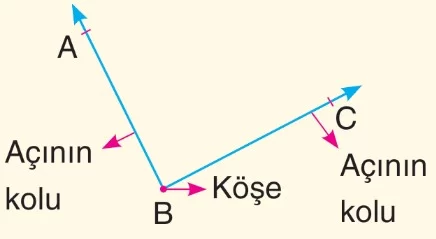
Açı:

Başlangıç noktaları aynı olan iki ışından oluşan şekle açı denir. Aşağıdaki ABC açısı, CBA açısı veya  şeklinde gösterilir. Aynı zamanda açı, bir ışının üzerindeki bir noktadan dışındaki bir noktaya gelene kadar yaptığı dönme miktarı olarak da tanımlanabilir.

Çember:

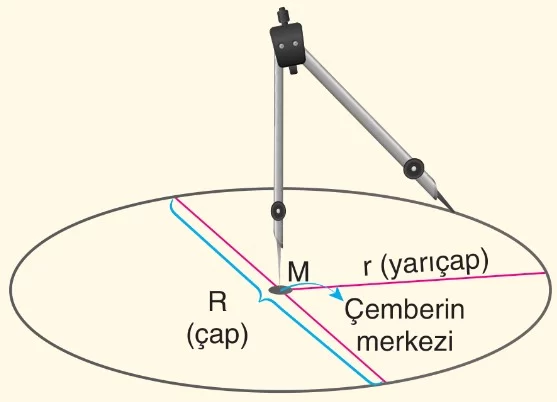
• Sabit bir noktaya eşit uzaklıkta bulunan noktaların oluşturduğu geometrik şekle çember denir. Çember çizmek için pergel kullanılır.
• Pergelle bir çember çizildiğinde pergelin sivri ucu çemberin merkezini, açıklığı ise çemberin yarıçapını gösterir.
• Çemberin merkezi ile çember üzerindeki herhangi bir noktayı birleştiren doğru parçasına yarıçap denir ve r harfi ile isimlendirilir.
• Çemberin merkezinden geçerek çember üzerindeki herhangi iki noktayı birleştiren doğru parçasına çap denir ve R harfi ile gösterilir.

Çember Çizimi:

Pergel kullanılırken önce pergelin kolları arasında rastgele bir açıklık oluşturulur. Daha sonra pergelin sivri ucu merkez kabul edilen bir noktaya konur ve sabitlenir. Pergelin kalem takılan diğer ucu bu sivri uç etrafında bir tam tur döndürülür.

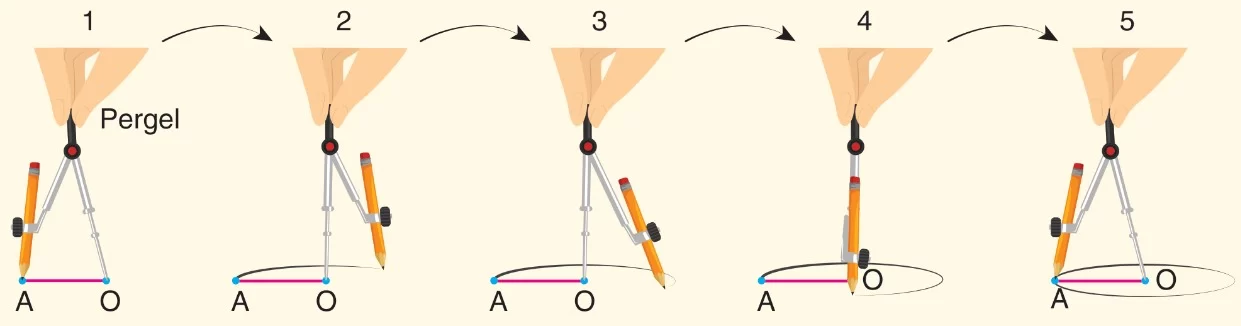
Böylece çember oluşturulur.

Doğruya Dikme Çizme:

• Bir doğruya dışındaki veya üzerindeki bir noktadan dik olarak çizilen doğru, doğru parçası veya ışına dikme denir.
• Bir doğru ile dışındaki bir noktayı birleştiren doğru parçalarından en kısa olanı bu noktadan doğruya çizilen dikmedir.
• Bir doğruya dışındaki bir noktadan dikme çizebilmek için gönye kullanılır.
• 
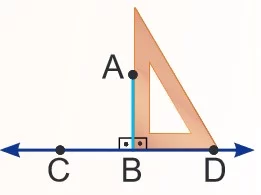
  Diklik “┴” sembolü ile gösterilir ve [AB] ┴ CD yazılır.

Bir Doğruya Dışındaki Bir Noktadan Dik Çizme:

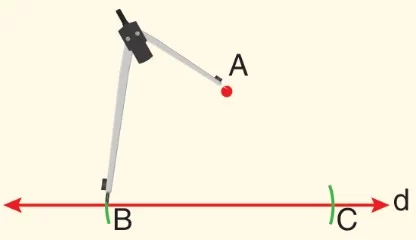
• Bir cetvel yardımı ile d doğrusu çizilir ve dışında bir A noktası belirlenir.

• Pergelin sivri ucunu A noktasına yerleştirip doğruyu iki noktada kesecek şekilde yay çizilir.

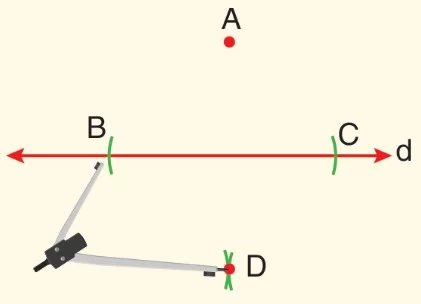
• Pergelin uçları arasındaki açıklığı değiştirmeden B ve C noktalarına sivri ucunu koyup iki yay çizilir. Kesim noktasına ise D ismi verilir.

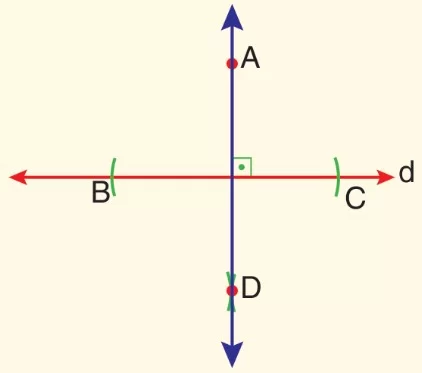
• Son olarak cetvel yardımıyla A ve D noktalarından geçecek şekilde bir doğru çizilir.

Düzlem: Düzlem, kenarları ve kalınlığı olmayan düz bir yüzeyin geometrik modelidir. Her yönden sonsuza kadar uzanır.