Üçgende Kenarortay (Ağırlık Merkezi) 9. Sınıf
Kenarortay konularını tekrar ettikten sonra “9. Sınıf Üçgende Kenarortay Çözümlü sorular ve testler” için bağlantıya tıklayabilirsiniz.
Kenarortay
-
Bir üçgenin kenarının orta noktası ile bu kenarın karşı köşesini birleştiren doğru parçasına kenarortay denir.
-
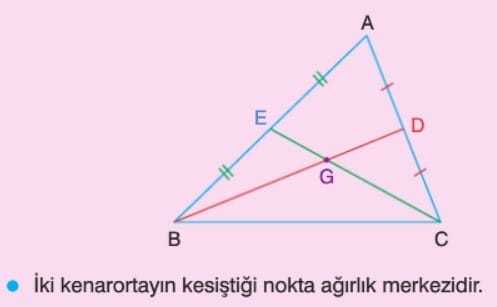
Üçgenin üç kenarortayı bir noktada kesişir.
-
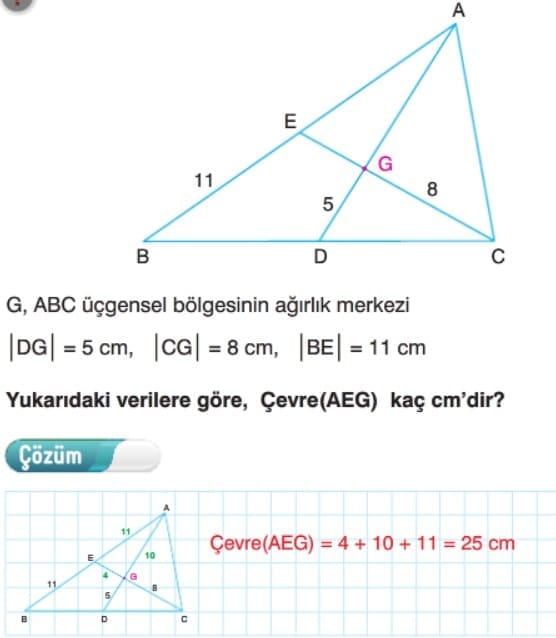
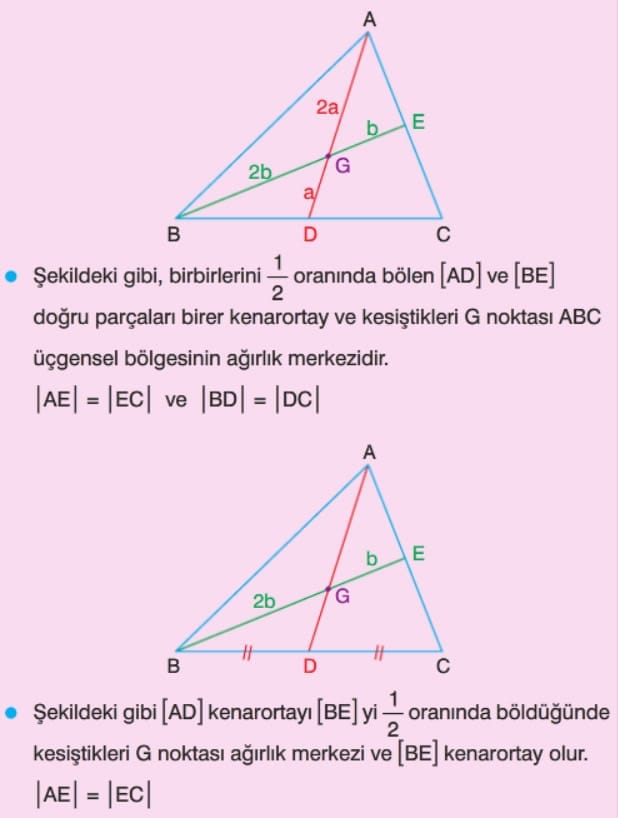
Kenarortayların kesim noktası (G noktası) ABC üçgensel bölgesinin ağırlık merkezidir.
-
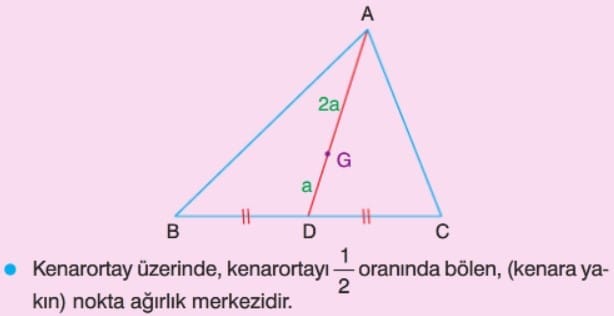
Üçgensel bölgenin ağırlık merkezi her zaman kenarortay üzerindedir. Ağırlık merkezi, kenarortayı kenara yakın şekilde 1’e 2 oranında böler.
Üçgende Kenarortay (Ağırlık Merkezi) Çözümlü Sorular
Çözümlü Örnek Test Soruları
Konu: Üçgende Kenarortay ve Ağırlık Merkezi
1. Bir üçgende kenarortayların kesişim noktası aşağıdakilerden hangisidir?
A) Diklik merkezi
B) Ağırlık merkezi
C) Çevrel çember merkezi
D) İç teğet çember merkezi
Cevap: B) Ağırlık merkezi
Çözüm: Bir üçgende kenarortaylar bir noktada kesişir ve bu noktaya ağırlık merkezi (G) denir. Ağırlık merkezi, üçgeni dengeleyen noktadır ve kenarortayları 2:1 oranında böler.
2. Bir ABC üçgeninde AG = 6 cm ve G noktası ağırlık merkezi ise, GA:AG oranı kaçtır?
A) 1:2
B) 2:1
C) 3:1
D) 1:3
Cevap: B) 2:1
Çözüm: Ağırlık merkezi, kenarortayları 2:1 oranında böler. Yani, AG = 2x ve GB = x olacak şekilde AG:GB = 2:1 oranı vardır.
3. Bir üçgenin ağırlık merkezi hangi doğru parçalarının kesişimiyle bulunur?
A) Kenarortaylar
B) Yükseklikler
C) Açortaylar
D) Kenar orta dikmeler
Cevap: A) Kenarortaylar
Çözüm: Üçgende kenarortaylar bir noktada kesişir ve bu noktaya ağırlık merkezi denir. Yüksekliklerin kesişimi diklik merkezi, açıortayların kesişimi iç teğet çember merkezi, kenar orta dikmelerin kesişimi ise çevrel çember merkezi olarak adlandırılır.
4. Bir ABC üçgeninde kenarortay uzunlukları aşağıdakilerden hangisine bağlıdır?
A) Sadece kenar uzunluklarına
B) Sadece açı ölçülerine
C) Kenar uzunlukları ve açı ölçülerine
D) Sadece üçgenin çevresine
Cevap: C) Kenar uzunlukları ve açı ölçülerine
Çözüm: Kenarortay uzunluğu, üçgenin kenar uzunluklarına ve iç açılarının büyüklüklerine bağlıdır. Kenar uzunlukları arttıkça kenarortaylar da uzayabilir.
5. Bir üçgende kenarortayların oluşturduğu ağırlık merkezi ile ilgili aşağıdaki ifadelerden hangisi yanlıştır?
A) Üçgenin her zaman iç bölgesindedir.
B) Kenarortayları 2:1 oranında böler.
C) Ağırlık merkezi, üçgenin kütle merkezi gibi davranır.
D) Ağırlık merkezi, her zaman üçgenin en uzun kenarında bulunur.
Cevap: D) Ağırlık merkezi, her zaman üçgenin en uzun kenarında bulunur.
Çözüm: Ağırlık merkezi her zaman üçgenin iç bölgesinde yer alır. Ancak belirli bir kenarda olması gerekmez, üçgenin genel şekline bağlı olarak farklı konumlarda olabilir. Bu yüzden D seçeneği yanlıştır.
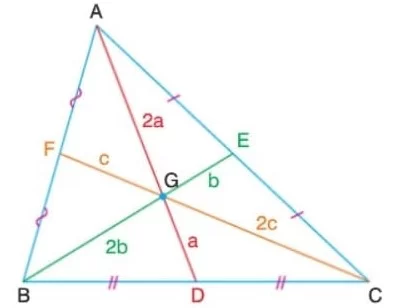
Bir üçgenin kenarortayları bir noktada kesişir. Bu nokta üçgenin ağırlık merkezidir. G noktası, ABC üçgeninin ağırlık merkezi olur. Bir üçgende bir köşeyi karşısındaki kenarın orta noktasına birleştiren doğru parçasına 0 kenara ait kenaortay denir.
[AD], [BC] kenarına ait kenarortaydır. Va ile gösterilir. Bir üçgende ağırlık merkezi üçgenin kenarortaylarını 2’ye 1
oranında böler. Yukarıdaki ABC üçgeninde;
|AG| =2|GF|, |BG| =2|GD| ve |CG| =2|GE| dir.
Bilgi: Bir üçgende iki kenara ait kenarortayın kesim noktası o üçgenin ağırlık merkezi olur. Üçüncü kenara ait olan kenarortay da o noktadan geçmek zorundadır.
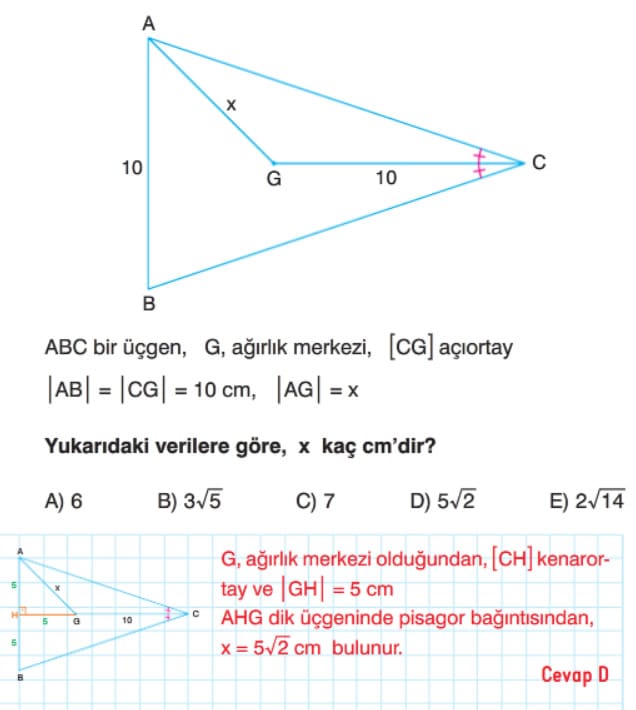
Çözüm: G ağırlık merkezi olduğundan [CG] yi uzatırsak [CH] kenarortay olur.
|AH| = |HB| =4 cm dir.
|GC| =6 cm ise
|HG| =3 cm dir.
[CH], hem açıortay hem de kenarortay olduğundan ABC üçgeni ikizkenar üçgen ve dolayısıyla [CH] doğru parçası [AB] doğru parçasına dik olur.
AHG (3 – 4 – 5) üçgeninden |AG| = 5 cm olur.
G ağırlık merkezi olduğundan
|AG| = 2|GD|
5 = 2 . x ise x = 2,5 cm bulunur.
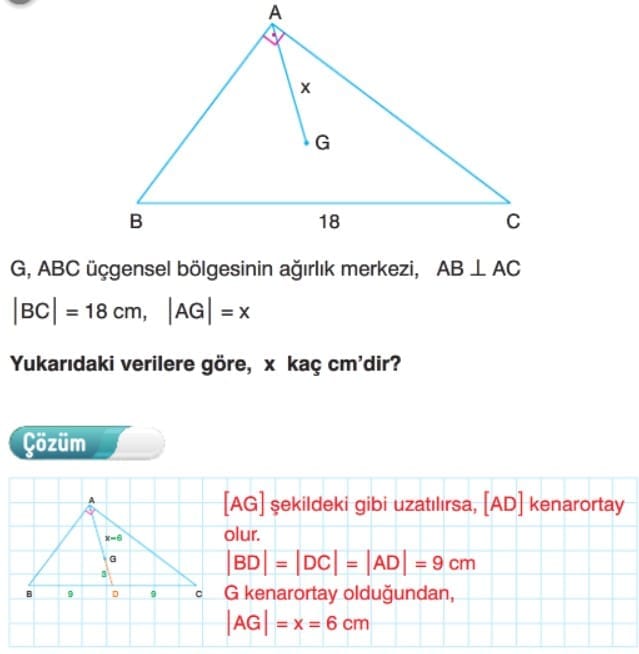
Çözüm: G ağırlık merkezi olduğundan [BD] kenarortay olur.
|AD| = |DC| = 12 cm dir.
ABC dik üçgen olduğundan
|BD| = 12 cm olur.
|BG| = 2|GD| olduğundan
|GD| = 4 cm ve |BG| = 8 cm bulunur.
Bilgi: Bir dik üçgende hipotenüse ait kenarortay hipotenüsün yarısına eşittir.
ABC dik üçgeninde |AD| = |DC| = |BD| dir. Eğer bir dik üçgende bu üç uzunluktan iki tanesi eşit ise üçüncüsü de eşit olur. Bu üç uzunluğun eşit olduğu üçgenler ise dik üçgen olur.
Kenarortayın Tanımı: Bir üçgenin bir kenarını ortadan iki eşit parçaya bölen doğruya “kenarortay” denir. Kenarortay, üçgenin bir kenarı üzerinde yer alır ve karşılık gelen açıyı iki eşit parçaya böler.
Kenarortayın Tarihçesi: Kenarortay konusu, antik Yunan matematikçilerinin çalışmalarına dayanmaktadır. Euclid’in “Elements” adlı eseri, üçgenlerin özellikleri üzerine detaylı bir inceleme sunar. Euclid, M.Ö. 300 civarında yaşamıştır ve geometri üzerine yazdığı eserleri, matematiksel bilginin temelini atmıştır.
Kenarortayın Özellikleri:
- Bir Kenarı İki Eşit Parçaya Böler: Kenarortay, bir üçgenin bir kenarını ortadan iki eşit parçaya böler. Bu, kenardaki iki üçgenin birbirine eşit olduğu anlamına gelir.
- Üçgenin Kenarı Üzerinde Yer Alır: Kenarortay, üçgenin bir kenarı üzerinde bulunur ve diğer iki kenarı ortalar.
- Üçgenin Karşılık Gelen Açısını İki Eşit Parçaya Böler: Kenarortay, üçgenin bir kenarındaki karşılık gelen açıyı iki eşit parçaya böler.