Denklem ve Eşitsizlik Sistemleri 11. Sınıf
1. iKiNCİ DERECEDEN İKİ BİLİNMEYENLİ DENKLEM SİSTEMLERİ
A) İkinci Dereceden İki Bilinmeyenli Denklemler
a, b, c, d, e, f gerçek sayılar ve a, b, c sayılarından en az ikisi sıfırdan farklı olsun.
ax2 + bxy + cy2 + dx + ey + f = 0
şeklindeki denklemlere ikinci dereceden iki bilinmeyenli denklem denir.
B) Denklem Sistemleri
İki bilinmeyenli en az iki denklemden oluşan denklem sisteminde, denklemlerden en az biri ikinci dereceden ise bu sisteme ikinci dereceden iki bilinmeyenli denklem sistemi denir.
Dikkat:
Denklem sistemindeki denklemlerin ortak çözümü de, denklem sisteminin çözüm kümesini verir. Bu çözüm kümesi genellikle sorularda ÇK ile gösterilir.
Örneğin;
x2 – y = – 10 (I)
2x – y = 7 (II)
denklem sisteminde II nolu denklemde
2x – y = 7 ve y = 2x -y
olduğundan I nolu denklemde y yerine 2x – 7 yazılıp çözüme gidilebilir.
2. İKİNCİ DERECEDEN BİR BİLİNMEYENLİ EŞİTSİZLİKLER
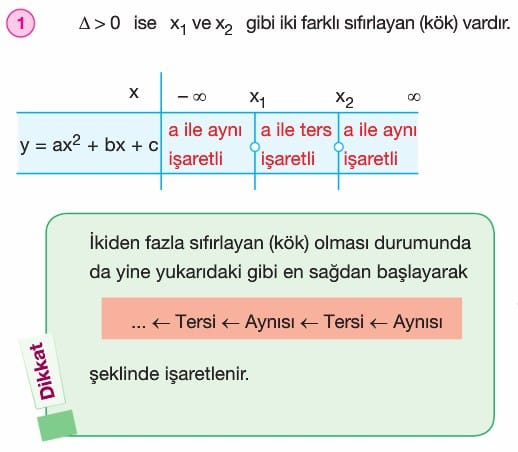
A) İkinci Dereceden Bir Bilinmeyenli Fonksiyonun İşareti
a ≠ 0 ve f: R → R olmak üzere
f(x) = y = ax2 + bx + c fonksiyonunun işareti aşağıdaki gibi incelenir.


B) İkinci Dereceden Bir Bilinmeyenli Eşitsizliklerin Çözümü
a, b, c ∈ R ve a ≠ 0 olmak üzere,
ax2 + bx + c > 0
ax2 + bx + c < 0
ax2 + bx + c ≥ 0
ax2 + bx + c ≤ 0
ifadelerinin her birine ikinci dereceden bir bilinmeyenli eşitsizlik denir. Çözüm yapılırken;
- Önce, f(x) = ax2 + bx + c fonksiyonunun işaret tablosu yapılır.
- Sonrada eşitsizliğin yönüne göre, tabloda belirtilen aralık çözüm kümesini oluşturur.

Dikkat:
a ∈ R+ olmak üzere
ax2 + bx + c = 0 denkleminin kökleri x1 ve x2 (x1 < x2) olsun.
- ax2 + bx + c < O eşitsizliğininin çözüm kümesi kökler arası, yani (x1, x2) aralığıdır.
- ax2 + bx + c > O eşitsizliğininin çözüm kümesi de kökler dışı yani (-∞, x1) u (x1, ∞) olur.
C) Eşitsizliğin Daima Sağlanması Durumu
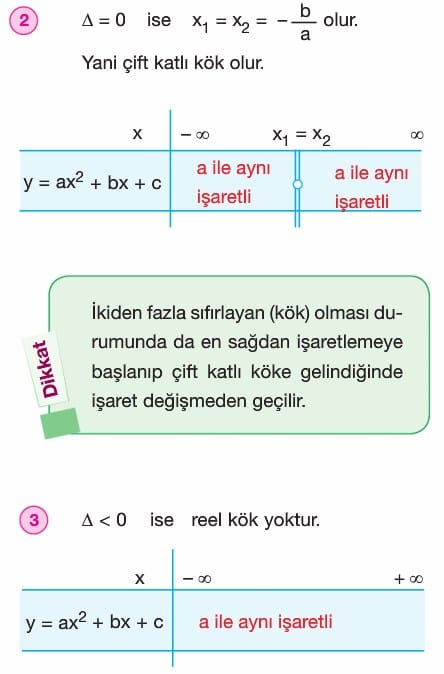
- ax2 + bx + c < 0 eşitsizliğinin daima (her x gerçek sayısı için) sağlanması için
Δ < 0 ve a < 0 olmalı. - ax2 + bx + c > 0 eşitsizliğinin daima (her x gerçek sayısı için) sağlanması için
Δ < 0 ve a > 0 olmalı.
D) Gerçek Sayılardaki Çözüm Kümesinin Boş Küme Olması Durumu
- ax2 + bx + c < 0 eşitsizliğinin gerçek sayılardaki çözüm kümesinin Ø olması için
Δ < 0 ve a > 0 olmalıdır. - ax2 + bx + c > 0 eşitsizliğinin gerçek sayılardaki çözüm kümesinin Ø olması için
- Δ < 0 ve a < 0 olmalıdır.
E) Poinomların Çarpımı Şeklindeki Eşitsizlikler
P(x) . Q(x) . R(x) < 0 veya
P(x) . Q(x) . R(x) > 0
şeklindeki eşitsizliklere ait işaret tablosu yapılırken
P(x) . Q(x) . R(x)
ifadesinin sıfırlayanları tabloda yerleştirilir. P(x), Q(x) ve R(x) ifadelerinin her birinin işaret durumuna göre çarpımın işareti bulunup, işaret tablosunda en sağdaki bölmeden başlayarak
… ← Aynısı ← Tersi ← Aynısı
şeklinde işaretlenir. Bu işaretlemede çift katlı köklere (çift miktarda olan köklere) dikkat edilir.
F) Polinomların Bölümü Şeklindeki Eşitsizlikler
P(x)Q(x)<0 veya P(x)Q(x)>0
gibi eşitsizliklere ait işaret tablosu yapılırken
P(x) = 0 ve Q(x) = 0 olmasını sağlayan x değerleri tabl
oda yerleştirilir.
P(x)Q(x)
ifadesinin işareti bulunup en sağ bölmeden başlayarak
… ← Aynısı ← Tersi ← Aynısı
şeklinde işaretlenir.
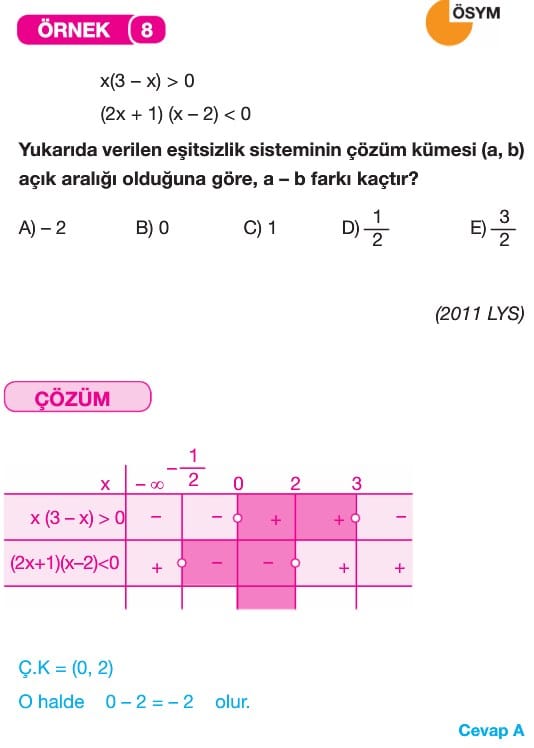
G) Eşitsizlik Sistemleri
Verilen bir eşitsizlik sisteminin çözümü bulunurken
- Her bir eşitsizliğin çözüm aralığı bulunur.
- Bulunan çözüm aralıklarının kesişim kümesi bulunur.
Bu kesişim kümesi eşitsizlik sisteminin çözüm kümesini oluşturur.
Çözümlü Örnek Test Soruları
Soru 1:
Bir mağazada A ürünü, B ürününden 10 TL daha pahalıdır. A ve B ürünlerinden toplam 5 adet alınmış ve 180 TL ödenmiştir. Buna göre, A ve B ürünlerinin fiyatlarını belirleyiniz.
A) A = 40 TL, B = 30 TL
B) A = 45 TL, B = 35 TL
C) A = 50 TL, B = 40 TL
D) A = 55 TL, B = 45 TL
E) A = 60 TL, B = 50 TL
Soru 2:
Verilen eşitsizliği çözünüz:
2x – 3 > 5
A) x > 4
B) x > 5
C) x > 3
D) x > 1
E) x > 6
Soru 3 (Yeni Nesil Soru):
Bir inşaat projesinde kullanılan çimento torbalarının ağırlığı standart olarak 50 kg’dır. İşçiler, yükleme sırasında torbaların bir kısmını yanlışlıkla yığmış ve torbaların yarısından fazlası 2 kg eksik ağırlıkla yüklenmiştir. Bu durumda, eksik yüklenen torba sayısı, toplam torba sayısının 1 bölü 3’ünden daha azdır. Toplam torba sayısı en az kaç olmalıdır?
A) 15
B) 18
C) 21
D) 24
E) 27
Soru 4:
x ve y birbirinden farklı iki sayıdır. x – y = 6 ve 2x + y = 14 olduğuna göre, x ve y kaçtır?
A) x = 10, y = 4
B) x = 8, y = 2
C) x = 12, y = 6
D) x = 7, y = 1
E) x = 6, y = 0
Soru 5:
Verilen denklemi çözünüz:
4x – 2(3x + 1) = 5x – 7
A) x = -5
B) x = 2
C) x = 1
D) x = -2
E) x = 3
Soru 6 (Yeni Nesil Soru):
Bir bahçede yetiştirilen elma ağaçları için sulama işlemi yapılmaktadır. Sulama işlemi, ağaç sayısına bağlı olarak değişen iki farklı yöntemle yapılmaktadır:
- Birinci yöntemde, her ağaç için 3 litre su kullanılır.
- İkinci yöntemde, ilk 10 ağaç için toplam 40 litre su, sonraki her ağaç için ise 2 litre su kullanılır.
Toplam 15 ağacın sulandığı bir bahçede, hangi yöntem daha fazla su harcar ve fark ne kadardır?
A) Birinci yöntem 15 litre daha fazla su harcar
B) İkinci yöntem 10 litre daha fazla su harcar
C) Birinci yöntem 5 litre daha fazla su harcar
D) İkinci yöntem 5 litre daha fazla su harcar
E) Fark yoktur, iki yöntem de eşit miktarda su harcar
Soru 7:
Verilen sistemin çözüm kümesini bulunuz:
x – 2y = 4
3x + y = 7
A) (2, -1)
B) (3, 1)
C) (4, 2)
D) (1, 0)
E) (0, -2)
Soru 8:
Bir üçgenin iç açılarının toplamı 180 derecedir. Bu üçgenin iki açısı eşit olup her biri x derecedir. Üçüncü açı ise x’in iki katı kadar olduğuna göre, x kaçtır?
A) 30
B) 40
C) 45
D) 50
E) 60
Soru 9 (Yeni Nesil Soru):
Bir çiftlikte inekler ve koyunlar bulunmaktadır. Çiftlikteki inek sayısının koyun sayısından 5 fazla olduğu ve toplamda 60 bacak olduğu bilinmektedir. Bir inek 4, bir koyun 2 bacaklı olduğuna göre, çiftlikte kaç koyun bulunmaktadır?
A) 8
B) 10
C) 12
D) 14
E) 16
Soru 10:
Bir sayının karesi, aynı sayının iki katına eşittir. Bu sayıyı bulunuz.
A) 0
B) 1
C) 2
D) 3
E) 4

















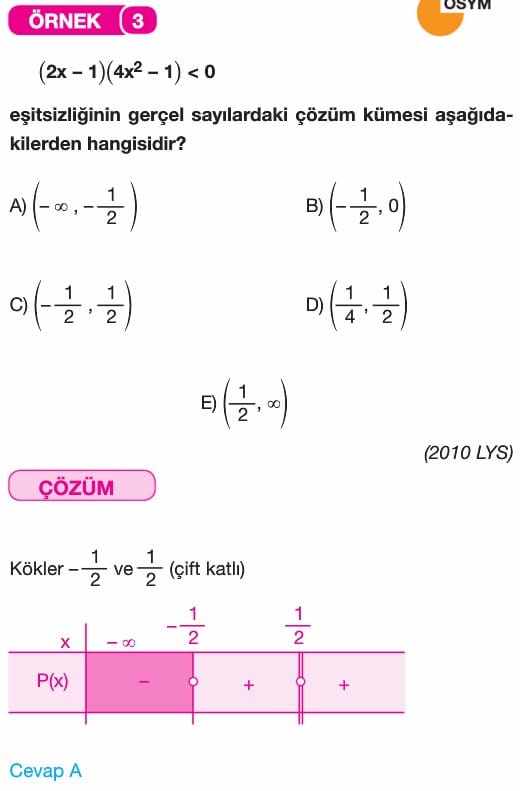




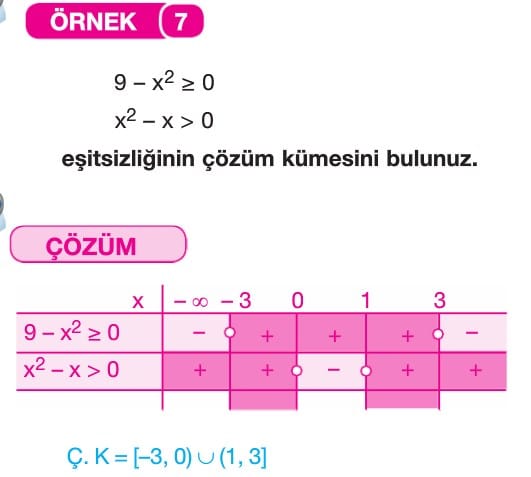



Örnek üçte parantez içerisinde ki ifadenin karesi ni Edebiyat hocası mı aldı ?
Cevap: (1-2y)^2 bu ifadeden bahsediyorsanız eğer bunun açılımında bir hata yok. 1-4y+4y^2
Tesekkurler super anlatilmis
teşekkür ederim