Matematikte sayma yöntemleri, belirli bir olayın kaç farklı şekilde gerçekleşebileceğini sistematik bir şekilde bulmamızı sağlar. Sayma yöntemleri, özellikle olasılık hesaplamalarının temelini oluşturur ve günlük hayatta karşılaşılan birçok problemde kullanılır. 10. sınıf matematik müfredatında, bu yöntemler öğrencilere olayların sıralanması, seçilmesi ve düzenlenmesiyle ilgili temel kavramları öğretir. Permütasyon, kombinasyon, çarpma ve toplama ilkeleri gibi başlıklarla, bir problemi farklı yaklaşımlarla çözme yetisi kazandırılır. Sayma yöntemleri, olayları daha hızlı ve doğru bir şekilde analiz etmeye yardımcı olur ve olasılık konusuna sağlam bir temel oluşturur. Bu giriş bölümünde, sayma yöntemlerinin mantığını kavramak ve bu yöntemlerin nasıl uygulanacağını öğrenmek için gerekli adımları inceleyeceğiz.

10. sınıf Sayma Yöntemleri Testleri

10. sınıf Sayma Yöntemleri Ders Notu

Toplama ve Çarpma Yöntemlerini Kullanarak Sayma

Toplama Yoluyla Sayma

Ayrık iki kümenin birleşiminin eleman sayısını toplama işlemi yaparak bulmaya, toplama yoluyla sayma yöntemi adı verilir. A ve B sonlu ve ayrık iki küme olmak üzere
s(A U B) = s(A) + s(B) dir.

Örneğin: Bir öğrencinin 5 farklı gömleği ve 4 farklı pantolonu vardır. Bu öğrenci 1 gömlek veya 1 pantolonu 5+4=9 farklı şekilde giyer.
Örneğin: Bir sınıfta 12 kız ve 14 erkek öğrenci vardır. Buna göre bu sınıfta toplam (12 + 14 = 26) öğrenci bulunmaktadır.

Çarpma Yoluyla Sayma

Ayrık iki kümenin kesişiminin eleman sayısını çarpma işlemi yaparak bulmaya, çarpma yoluyla sayma yöntemi adı verilir.

m herhangi bir işlemin gerçekleşme yollarının sayısını, n de ikinci bir işlemin gerçekleşme yollarının sayısını göstersin. m yoldan birisi ile yapılan ilk işlemden sonra ikinci işlem n yolla yapılabiliyorsa bu iki işlem birlikte m.n yolla yapılabilir. Bu durum işlem sayısı arttığında da geçerlidir. Yani; A, B ve C boş olmayan ayrık birer küme olmak üzere,

i) A ve B kümelerinden birer eleman seçerek oluşturulabilecek tüm sıralı ikililerin sayısı;
s(AxB) = s(A) . s(B)

ii) A, B ve C kümelerinden birer eleman seçilerek oluşturulacak tüm sıralı üçlülerin sayısı;
s(AxBxC) = s(A) . s(B) . s(C)

şeklinde çarpma işlemi ile bulunur.

Sonraki Konu: Faktöriyel

Sayma Yöntemleri Soru Çözümleri

Not:

Rakamları tekrarlı sayılar yazılırken

• Her bir rakamın her bir basamağa yazılabileceği unutulmamalıdır.
• Bir şart verilmişse şartın olduğu basamak öncelikle ele alınır.
• Verilen elemanlar arasında o varsa yazılacak sayının ilk basamağına 0 gelemeyeceği dikkate alınmalıdır.
• Her basamağa yazılabilecek rakam adetleri çarpılarak sonuç hesaplanır.

Rakamları tekrarsız sayılar yazılırken

• Soruda şart varsa öncelikle şartın olduğu basamak ele alınır.
• Verilen elemanlar içinde 0 varsa ilk basamağa 0 yazılamaz.
• Her bir basamakta kullanılabilecek rakam sayısı özel durumlar yoksa bir azaltılır.
• Her basamağa yazılabilecek rakam adetleri çarpılır.

1. ÜNİTE: SAYMA VE OLASILIK

A. Sıralama ve Seçme

• Sayma Yöntemleri
• Faktöriyel
• Permütasyon
• Tekrarlı Permütasyon
• Kombinasyon
• Pascal Üçgeni ve Binom Açılımı

B. Basit Olayların Olasılıkları

• Basit Olayların Olasılıkları

Çözümlü Örnek Test Soruları

Soru 1:
Bir tiyatro kulübünde 5 erkek ve 3 kız vardır. Bu kulüpten bir erkek ve bir kız seçilerek bir gösteri yapılacaktır. Kaç farklı seçim yapılabilir?

A) 8
B) 12
C) 15
D) 20
E) 30

Çözüm:
Bir erkek 5 farklı şekilde, bir kız 3 farklı şekilde seçilebilir. Bu durumda toplam seçim sayısı 5 * 3 = 15’tir.

Doğru Cevap: C

Soru 2:
Bir okuldaki kütüphanede 4 tarih, 3 edebiyat ve 2 coğrafya kitabı bulunmaktadır. Bir tarih, bir edebiyat ve bir coğrafya kitabı kaç farklı şekilde seçilebilir?

A) 9
B) 12
C) 18
D) 24
E) 36

Çözüm:
Bir tarih kitabı 4 farklı, bir edebiyat kitabı 3 farklı ve bir coğrafya kitabı 2 farklı şekilde seçilebilir.
Toplam seçim sayısı: 4 * 3 * 2 = 24.

Doğru Cevap: D

Soru 3:
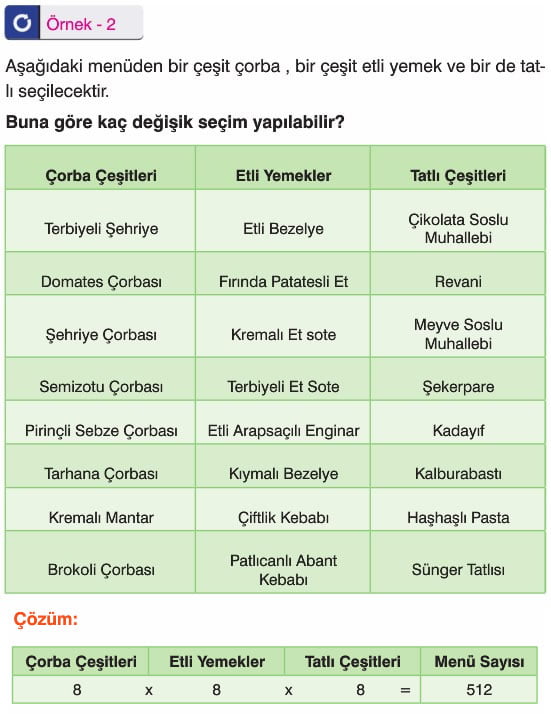
Bir restoranda 3 çorba, 5 ana yemek ve 4 tatlı çeşidi bulunmaktadır. Bir çorba, bir ana yemek ve bir tatlıdan oluşan kaç farklı yemek kombinasyonu yapılabilir?

A) 12
B) 24
C) 60
D) 70
E) 80

Çözüm:
Bir çorba 3 farklı, bir ana yemek 5 farklı ve bir tatlı 4 farklı şekilde seçilebilir.
Toplam seçim sayısı: 3 * 5 * 4 = 60.

Doğru Cevap: C

Soru 4:
Bir öğrencinin 5 farklı matematik, 4 farklı fizik kitabı bulunmaktadır. Bir matematik ve bir fizik kitabı seçme sayısı kaçtır?

A) 9
B) 15
C) 20
D) 25
E) 30

Çözüm:
Bir matematik kitabı 5 farklı, bir fizik kitabı ise 4 farklı şekilde seçilebilir.
Toplam seçim sayısı: 5 * 4 = 20.

Doğru Cevap: C

Soru 5:
Bir markette 6 farklı meyve ve 4 farklı sebze bulunmaktadır. Bir meyve ve bir sebzeden oluşan bir alışveriş kombinasyonu kaç farklı şekilde yapılabilir?

A) 10
B) 12
C) 20
D) 24
E) 30

Çözüm:
Bir meyve 6 farklı, bir sebze ise 4 farklı şekilde seçilebilir.
Toplam seçim sayısı: 6 * 4 = 24.

Doğru Cevap: D

Soru 6:
Bir tiyatro oyununda 3 farklı başrol, 2 farklı yardımcı rol bulunmaktadır. Bir başrol ve bir yardımcı rolden oluşan kaç farklı oyuncu seçimi yapılabilir?

A) 5
B) 6
C) 8
D) 9
E) 10

Çözüm:
Bir başrol 3 farklı, bir yardımcı rol ise 2 farklı şekilde seçilebilir.
Toplam seçim sayısı: 3 * 2 = 6.

Doğru Cevap: B

Soru 7:
Bir spor takımı 4 farklı forma ve 3 farklı şort kullanmaktadır. Bir forma ve bir şorttan oluşan kaç farklı kombinasyon yapılabilir?

A) 6
B) 7
C) 10
D) 12
E) 15

Çözüm:
Bir forma 4 farklı, bir şort ise 3 farklı şekilde seçilebilir.
Toplam seçim sayısı: 4 * 3 = 12.

Doğru Cevap: D

Soru 8:
Bir giyim mağazasında 5 farklı tişört ve 4 farklı pantolon bulunmaktadır. Bir tişört ve bir pantolondan oluşan kaç farklı kombinasyon yapılabilir?

A) 9
B) 10
C) 15
D) 20
E) 25

Çözüm:
Bir tişört 5 farklı, bir pantolon ise 4 farklı şekilde seçilebilir.
Toplam seçim sayısı: 5 * 4 = 20.

Doğru Cevap: D

Soru 9:
Bir öğrenci, 6 farklı kalem ve 3 farklı silgi arasından bir kalem ve bir silgi seçmek istiyor. Kaç farklı seçim yapılabilir?

A) 8
B) 12
C) 15
D) 18
E) 20

Çözüm:
Bir kalem 6 farklı, bir silgi ise 3 farklı şekilde seçilebilir.
Toplam seçim sayısı: 6 * 3 = 18.

Doğru Cevap: D

Soru 10:
Bir sınıfta 7 kız ve 5 erkek öğrenci bulunmaktadır. Bu sınıftan bir kız ve bir erkek öğrenci kaç farklı şekilde seçilebilir?

A) 12
B) 24
C) 30
D) 35
E) 40

Çözüm:
Bir kız 7 farklı, bir erkek ise 5 farklı şekilde seçilebilir.
Toplam seçim sayısı: 7 * 5 = 35.

Doğru Cevap: D

Soru: Bir restoranda 5 çeşit yemek, 3 çeşit salata ve 4 çeşit tatlı bulunmaktadır. Ali, bir yemek, bir salata ve bir tatlı sipariş verecektir. Ancak Ali, sadece birinci ve dördüncü yemekleri seçerse tatlı olarak sadece ikinci ve üçüncü tatlıları seçebilmektedir. Diğer yemekler için herhangi bir tatlı seçme kısıtlaması yoktur. Ali’nin kaç farklı şekilde sipariş verebileceğini bulun.

Çözüm:

Eğer Ali birinci veya dördüncü yemekleri seçerse, tatlı olarak sadece ikinci ve üçüncü tatlıları seçebilir. Bu durumda:

• Yemek için 2 seçenek (birinci ve dördüncü yemek),
• Tatlı için 2 seçenek (ikinci ve üçüncü tatlı),
• Salata için herhangi bir kısıtlama olmadığından 3 seçenek vardır. Bu kısıtlı durumda toplam seçenek sayısı:
  2×3×2=12

Eğer Ali diğer yemekleri (ikinci, üçüncü veya beşinci) seçerse, tatlı seçimi serbesttir. Bu durumda:

• Yemek için 3 seçenek,
• Tatlı için 4 seçenek,
• Salata için yine 3 seçenek vardır. Bu durumda toplam seçenek sayısı:
  3×3×4=36

Sonuç olarak toplam farklı sipariş sayısı: 12+36=48

Soru: Bir spor salonunda 6 farklı koşu bandı, 4 farklı ağırlık makinesi ve 3 farklı bisiklet bulunmaktadır. Spor salonunda aynı anda 3 kişi egzersiz yapacaksa, her kişi farklı bir alet kullanmak zorundadır. Bu 3 kişinin egzersiz yapma kombinasyonları kaç farklı şekilde olabilir?

Çözüm: Bu durumda her kişi farklı bir cihaz kullanacağından, seçenekler şu şekilde olacaktır:

• Koşu bandı için 6 seçenek,
• Ağırlık makinesi için 4 seçenek,
• Bisiklet için 3 seçenek vardır.

Toplamda: 6×4×3=72 farklı kombinasyon oluşur.