Geometri, matematiksel düşünme ve uzayda nesnelerin özelliklerini anlama becerisini geliştiren önemli bir disiplindir. 5. sınıf seviyesinde, temel geometrik çizimlerle tanışmak öğrenciler için şekilleri kavrama, ölçme ve inşa etme yeteneklerini güçlendirmede ilk adımdır. Bu konu, açı, doğru, çokgen, daire ve simetri gibi temel kavramların öğrenilmesi ve bunların nasıl çizileceği üzerine yoğunlaşır.

5. Sınıf Temel Geometrik Çizimlerin Özellikleri Testleri

5. Sınıf Temel Geometrik Çizimlerin Özellikleri Ders Notu (2024 – 2025 Yeni Müfredat)

• Bir noktadan sonsuz sayıda doğru çizilebilir.

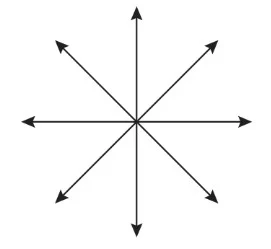
• İki noktadan yalnızbir tane doğru çizilebilir.

Dikme

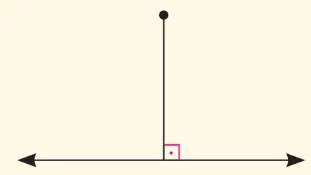
• Bir doğruya dışındaki bir noktadan yalnız bir dikme çizilebilir. Dikme, noktadan doğruya çizilebilecek en kısa doğru parçasıdır.

• Bir doğruya dışındaki farklı noktalardan eşit veya farklı uzunluklarda dikmeler çizilebilir. Çizgeç ile d doğrusu ve A, B, C noktaları çizelim.

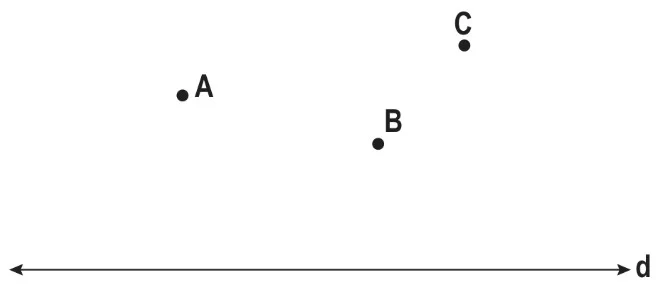
Gönye kullanarak A, B ve C noktalarından d doğrusuna dikmeler çizelim.

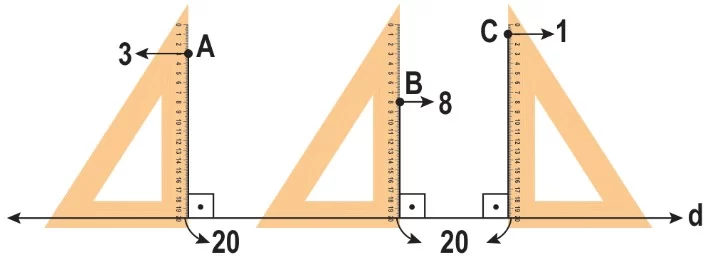
A’dan çizilen dikme uzunluğu 17 cm, B’den çizilen dikme uzunluğu 12 cm, C’den çizilen dikme uzunluğu 19 cm olan dikmeler farklı uzunlukta olabilir.

Eş Doğru Parçaları

Pergel ve cetvel yardımıyla eş doğru parçaları elde edebiliriz.

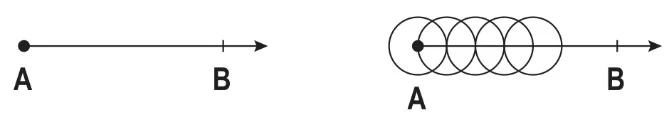
Bir doğru üzerinde pergel yardımıyla çemberler çizerek eşit uzunlukta doğru parçaları oluşturulabilir. Bu çizim yapılırken doğru üzerinde bir nokta alınır ve çember çizilir. Pergelin açıklığı değiştirilmeden ve merkezi ilk çemberin doğru ile kesişim noktası olan diğer çemberler çizilir. Çemberlerin yarıçapları eşit olacağından, istenildiği kadar eş doğru parçası oluşturulabilir.

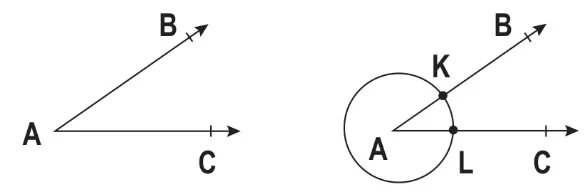
Merkezi A noktası olan bir çember çizilir. Çemberin ışınları kestiği noktalara K ve L noktaları işaretlenir. |AK| = |AL| olduğu görülür.
A açısının kollarından eşit uzunlukta doğru parçaları elde edilebilir.

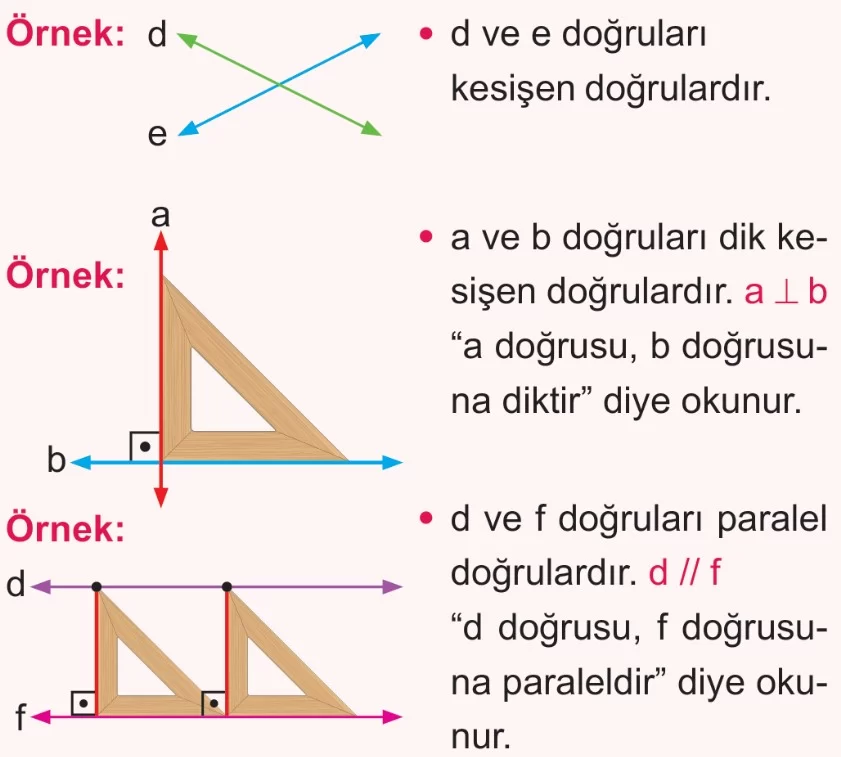
Paralel Doğrular ve Kesişen Doğrular

• Birbirinin dikmesi olan doğrular, ortak bir noktada kesişirler. İşte bu şekilde ortak bir noktada kesişen doğrulara kesişen doğrular denir.
• Kesişen doğruların arasındaki açı 90° ise bu doğrulara dik kesişen doğrular denir. Diklik “⊥” sembolü ile gösterilir.
• Bir doğruya, eşit uzaklıkta ve aynı doğrultudaki noktalar bir doğru oluşturulur. Bu iki doğru arasındaki uzaklık değişmediği için bu doğrulara paralel doğrular denir. “//” paralellik sembolüdür. d // m şeklinde gösterilir ve “d doğrusu, m doğrusuna paraleldir.” şeklinde okunur.

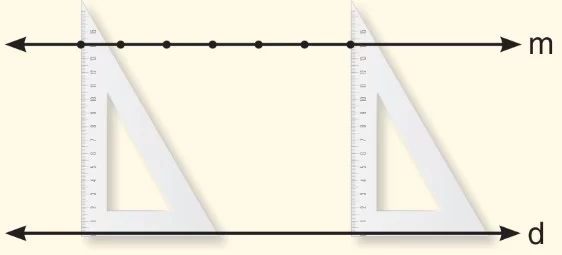
Aşağıdaki d doğrusu üzerine gönyeyle eşit uzunlukta noktalar çizelim.

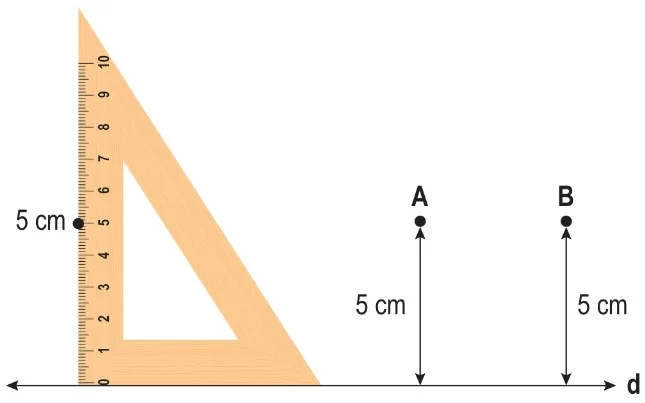
Bir çizgeç yardımıyla d doğrusuna eşit uzaklıktaki noktaları birleştirerek m doğrusunu oluşturalım.

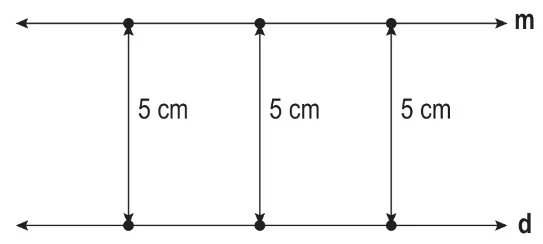
m doğrusu ile d doğrusu birbirine paralel doğrular olup m // d sembolü ile gösterilir.

Çözümlü Örnek Test Soruları

Soru 1:

Bir kareyi düzgün bir şekilde dört eş parçaya ayırmak için kaç doğru çizilir? Çizdiğiniz doğrular karenin hangi özelliklerine göre çizilmelidir?

Çözüm:
Bir kareyi dört eş parçaya ayırmak için iki doğru çizilmelidir. Bu doğrulardan biri, karenin yatay orta noktasından geçerken diğeri dikey orta noktasından geçmelidir. Bu doğrular karenin kenarlarına dik olmalı ve birbirini karenin merkezinde kesmelidir. Böylece kare, dört eşit küçük kareye bölünmüş olur.

Cevap: 2 doğru çizilmelidir.

Soru 2:

Bir düzgün altıgenin iç açılarının her biri kaç derecedir? Düzgün altıgenin çizimi yapılırken hangi geometrik şekilden faydalanılır?

Çözüm:
Düzgün altıgenin her bir iç açısını bulmak için çokgenlerde iç açı formülünü kullanırız:

Bir düzgün çokgenin iç açılarının toplamı = (n – 2) × 180°
Altıgen için n = 6 olduğundan:

İç açı toplamı = (6 – 2) × 180° = 4 × 180° = 720°

Her bir iç açı:
720° ÷ 6 = 120°

Düzgün altıgenin çizimi yapılırken, genellikle eşkenar üçgenlerden faydalanılır. Çünkü altıgen, merkezden geçen doğrularla altı eşit üçgene bölünebilir.

Cevap: Her bir iç açı 120°’dir ve çizim için eşkenar üçgenlerden faydalanılır.

Soru 3:

Bir dikdörtgenin köşegenleri çizildiğinde elde edilen üçgenler ne tür üçgenlerdir? Dikdörtgenin köşegenlerinin uzunlukları nasıl bulunur?

Çözüm:
Bir dikdörtgenin köşegenleri çizildiğinde, dikdörtgen dört eş üçgene bölünür. Bu üçgenlerin her biri ikizkenar dik üçgendir çünkü dikdörtgenin köşegenleri birbirine eşit ve kenarları dik keser.

Köşegen uzunluğu, Pisagor teoremi kullanılarak bulunabilir. Eğer dikdörtgenin kısa kenarı a, uzun kenarı b ise köşegenin uzunluğu:

Köşegen = √(a² + b²)

Cevap: İkizkenar dik üçgenler oluşur, köşegen uzunluğu Pisagor teoremi ile bulunur.

Soru 4:

Bir eşkenar üçgenin kenar uzunluğu 6 cm’dir. Bu üçgenin yüksekliği kaç santimetredir? (√3 = 1.73 alın)

Çözüm:
Eşkenar üçgende yükseklik, bir kenarı ortadan iki eşit parçaya böler ve 90° açı oluşturur. Yüksekliği bulmak için Pisagor teoremini kullanabiliriz. Bir kenarın yarısı, yükseklik ve eşkenar üçgenin kenarı üçgen oluşturur:

Kenarın yarısı = 6 cm ÷ 2 = 3 cm
Pisagor teoremi:
6² = 3² + yükseklik²
36 = 9 + yükseklik²
yükseklik² = 36 – 9
yükseklik² = 27
yükseklik = √27 = 5.2 cm (yaklaşık)

Cevap: Yükseklik yaklaşık 5.2 cm’dir.

Soru 5:

Bir çemberin çapı ile çevresi arasındaki ilişkiyi açıklayınız. Eğer bir çemberin çapı 10 cm ise, bu çemberin çevresi kaç santimetredir? (π = 3.14 alın)

Çözüm:
Bir çemberin çevresi, çap ile π sayısının çarpımıyla bulunur. Çevre formülü:

Çevre = π × çap

Eğer çemberin çapı 10 cm ise, çevresi:

Çevre = 3.14 × 10 cm
Çevre = 31.4 cm

Cevap: Çevre 31.4 cm’dir.

Alternatif Bilgi:

Paralel Doğruların Özellikleri

1. Aynı Düzlemde Bulunurlar: Paralel doğrular, mutlaka aynı düzlem üzerinde yer almalıdır. Farklı düzlemlerde bulunan doğrular, birbirleriyle kesişmeseler bile paralel olarak kabul edilmez.
2. Eşit Uzaklık: Paralel doğruların tüm noktaları arasında sabit bir uzaklık vardır. Bu uzaklık hiçbir zaman değişmez.
3. Hiçbir Zaman Kesişmezler: Paralel doğrular sonsuza kadar uzatıldığında bile hiçbir noktada birbirleriyle kesişmezler.
4. Aynı Yönde İlerlerler: Paralel doğrular, aynı yönde ilerler ve yönleri birbirine zıttı ya da farklı olmaz.

Paralel Doğruların Günlük Yaşamda Kullanımı

Paralel doğruların birçok farklı kullanım alanı vardır. Örneğin:

• Demiryolları: Tren rayları paralel doğrulara örnek olarak gösterilebilir. Raylar, aynı doğrultuda ilerler ve birbirlerine hiçbir zaman yaklaşmazlar.
• Binaların Cepheleri: Birçok bina tasarımında paralel çizgiler kullanılır. Bina duvarları, mimari açıdan paralel çizgilerle tasarlanır ve bu, yapıya estetik bir denge kazandırır.
• Yol Şeritleri: Karayollarında görülen şeritler de paralel doğrulardır. Şeritler, araçların düzenli bir şekilde hareket etmesini sağlar.

Paralel Doğruların Çizimi

Paralel doğrular, çizim sırasında cetvel ve gönye gibi araçlar kullanılarak oluşturulabilir. İki doğrunun paralel olduğunu doğrulamak için aralarındaki mesafenin her noktada eşit olup olmadığını ölçmek gerekir.

Çizim adımları şu şekildedir:

• Cetvel yardımıyla bir doğru çizin.
• Doğruya belirli bir uzaklıkta başka bir doğru çizin.
• Bu iki doğrunun her noktasındaki mesafeyi ölçerek paralel olup olmadığını kontrol edin.