İkizkenar Üçgen 9. Sınıf
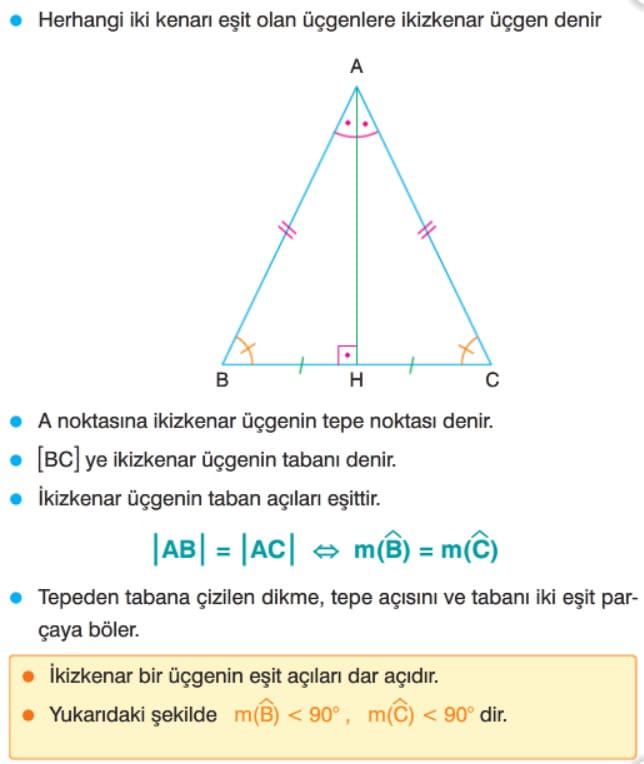
İkizkenar Üçgen Çözümlü Sorular
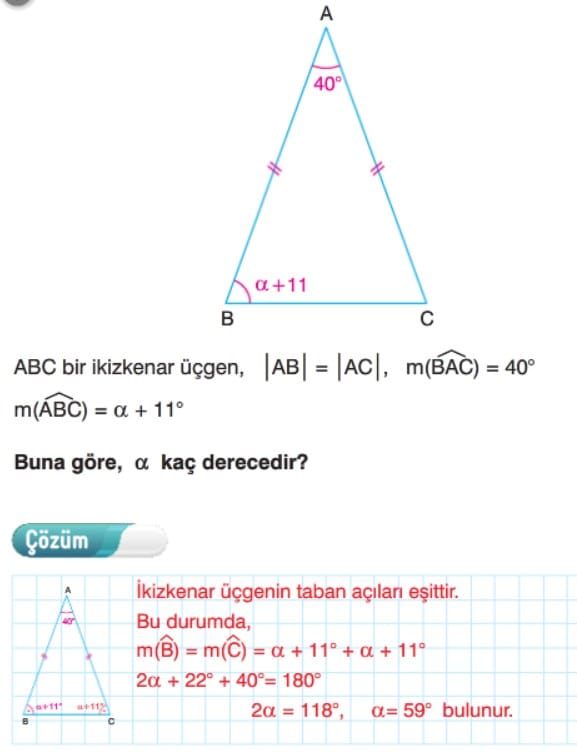
İkizkenar Üçgen konu anlatımı çözümlü sorular 9.sınıf matematik tyt
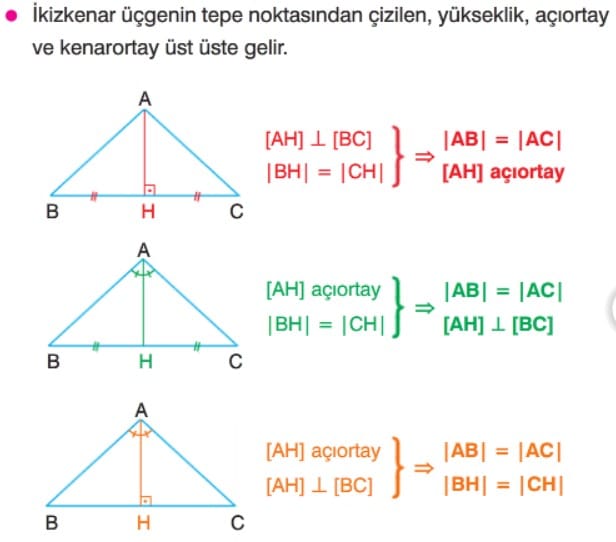
Bir ikizkenar üçgende tepe noktasından çizilen açıortay, kenarortay ve yükseklik çakışıktır. Bir üçgende bu üç yardımcı elemandan iki tanesi aynı doğru parçası ise bu üçgen ikizkenardır. Herhangi bir açısının ölçüsü 60° olan bir ikizkenar üçgen eşkenardır.
[BD] yi uzatarak [AC] yi kestiği noktaya H diyelim. İkizkenar üçgende tepe açısından çizilen açıortay, tabana hem dik hem de iki eşit parçaya böler.
Çözüm: O halde [BH] diktir [AC] ve |AH| = |HC| olur. ABH veya BCH dik üçgeninde pisagor bağıntısından,
|BH| = 12 cm olur.
|DH| = 12 - 9 = 3 cm dir.
ADH dik üçgeninde pisagor bağıntısından
x = kök 34 bulunur.
Çözüm: İkizkenar üçgenin tepe açısından çizilen yükseklik aynı zamanda kenarortay ve BC uzunluğu da 16 cm olduğundan dolayı AH yüksekliğini çizersek BH = HC = 8 cm ve DH uzunluğu da 2 cm olur. ADH dik üçgeninde pisagor teoremini kullanırsak AC uzunluğunun karesi 36 ya eşit çıkar. Buradan AH = 6 cm olur. AHC dik üçgeninde pisagor bağıntısından AC uzunluğu 10 cm bulunur. Buradan ABC üçgeninin çevresinin uzunluğu 36 cm bulunur.
30° nin karşısındaki dik kenar hipotenüs uzunluğunun yarısına; 60° nin karşısındaki dik kenar ise, 30° nin karşısındaki kenarın kök 3 katına eşittir. Bir dik üçgende, dik kenarlardan birinin uzunluğu hipotenüsün yarısı ise, bu bir 30° - 60° - 90° dik üçgenidir. Bir dik üçgende, dik kenarlardan birinin uzunluğu diğerinin kök 3 katı ise, bu bir 30° - 60° - 90° dik üçgenidir.