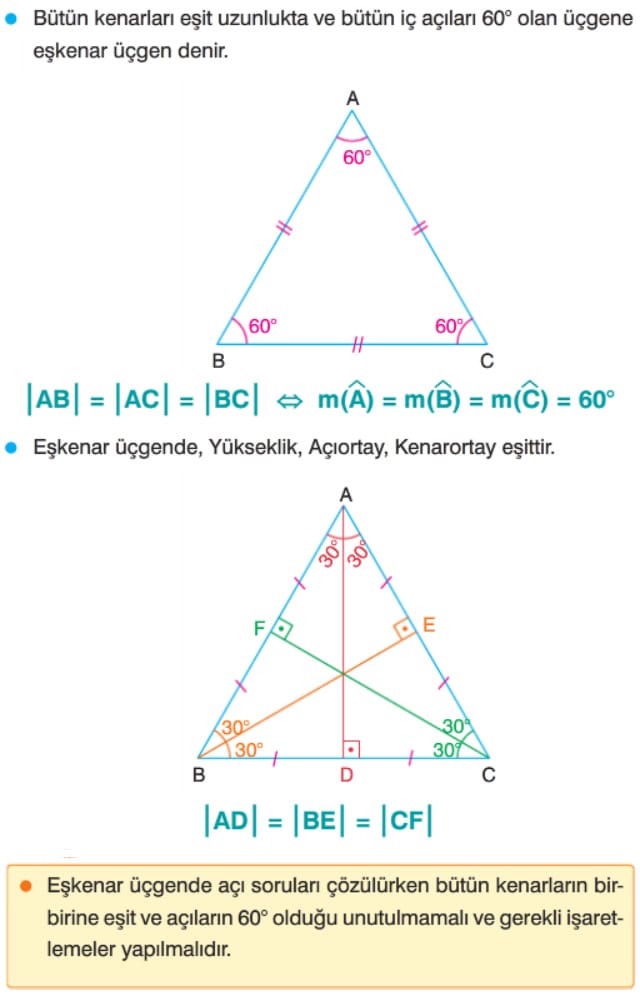
Eşkenar Üçgen konu anlatımı Çözümlü Sorular 9.sınıf matematik tyt

Üç kenarı birbirine eş ve iç açılarının her birinin ölçüsü 60° dir. Herhangi bir yükseklik eşkenar üçgeni iki tane (30°, 60°, 90°) üçgenine ayırır. Eşkenar üçgenin bir kenarına a dersek,
|BH| = |HC| = a / 2 ve |AHl=a kök 3 / 2 olur.
Eşkenar üçgenin yükseklikleri, açıortayları ve kenarortayları eşittir.
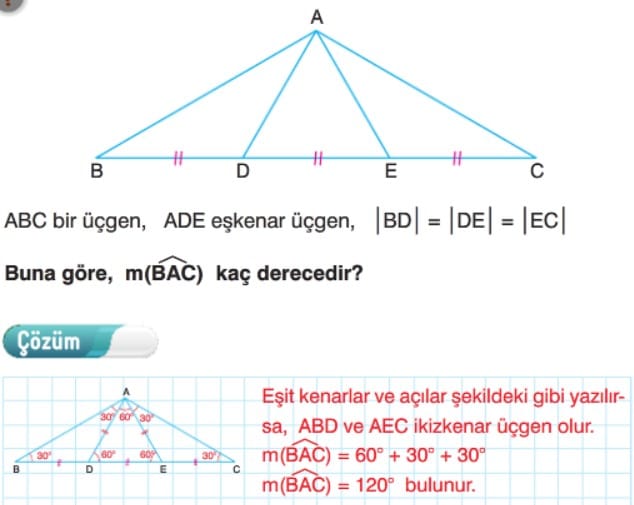
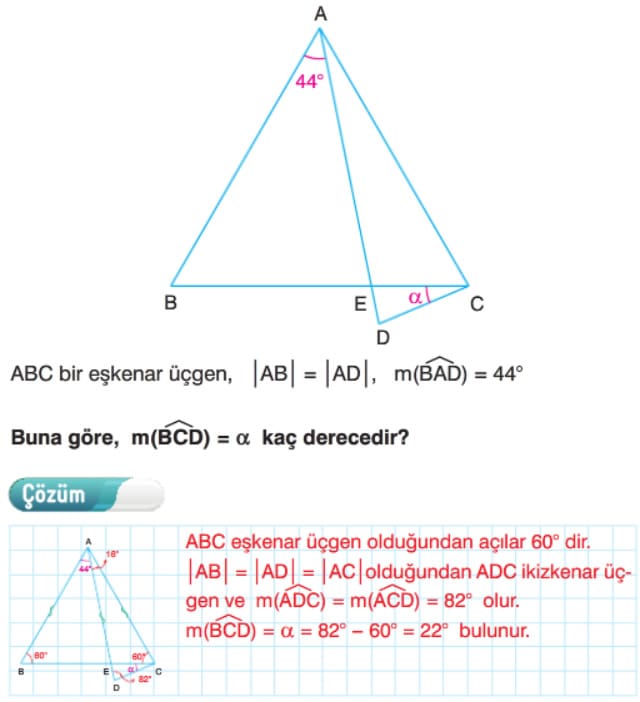
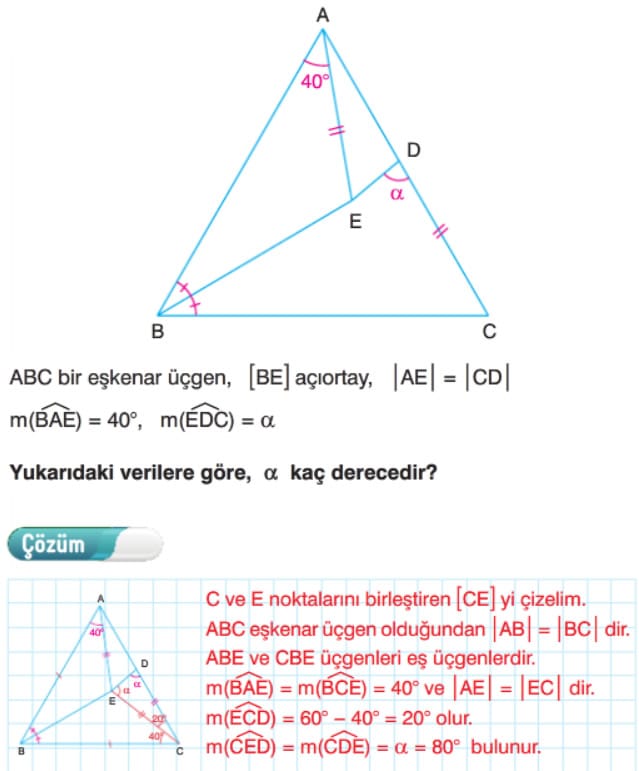
Çözüm: Eşkenar üçgenin açılarını 60° olarak yazarsak
m(AFD) = m(EFC) = m(E) = 30° olur.
Buradan, |CF| = |CE| = 5 cm olur.
ADF --> (30° - 60° - 90°) dik üçgeninde;
|AD| = 4 cm ise |AF| = 8 cm olur.
|AB| = |AC| olacağından
4 + x = 13
x = 9 cm bulunur.
Çözüm: [AH] yüksekliğini çizersek aynı zamanda kenarortay olur.
|BC| = 8 cm olduğundan,
|BH| = |HC| =4 cm ve
|HD| = 3 cm olur.
ABH (30° - 60° - 90°) dik üçgeninde, |AH| = 4 kök 3 cm,
AHD dik üçgeninde pisagor bağıntısından,
|AD| uzunluğu kök 57 cm bulunur.
Örnek: Bir eşkenar üçgenin iç bölgesinde alınan bir noktadan kenarlara dikmeler çiziliyor. Bu dikmelerin uzunlukları toplamı 12 cm olduğuna göre, eşkenar üçgenin çevresini bulalım.
Çözüm: Eşkenar üçgenin iç bölgesinde alınan bir noktadan kenarlara çizilen dikmelerin uzunlukları toplamı eşkenar üçgenin yüksekliğine eşittir. O halde verilen eşkenar üçgenin yüksekliği 12 cm dir. Bir kenarı a ve yüksekliği h olan bir eşkenar üçgende
h = a kök 3 / 2 ise 12 = a kök 3 / 2 olur.
Buradan a = 8 kök 3 cm ve
Çevre = 3a = 3 . 8 kök 3 = 24 kök 3 cm bulunur.

Soru: Bir eşkenar üçgenin bir kenarının uzunluğu 8 cm ise, bu üçgenin çevresini bulunuz.
Çözüm: Eşkenar üçgenin üç kenarı birbirine eşit olduğundan, çevresi üç kenarın toplamıdır. Çevre = 3 * Kenar Uzunluğu Çevre = 3 * 8 cm = 24 cm

Soru: Bir eşkenar üçgenin iç açıları toplamı kaç derecedir?
Çözüm: Eşkenar üçgenin iç açıları eşit olduğundan, her bir açı 60 derecedir. İç açıları toplamı: 60 + 60 + 60 = 180 derece

Soru: Bir eşkenar üçgenin bir iç açısının ölçüsü 40 derece ise, diğer iki iç açının ölçüsü nedir?
Çözüm: Eşkenar üçgenin iç açıları eşit olduğundan, diğer iki açı da 40 derecedir.