Fonksiyonlar, matematiğin en temel ve en önemli kavramlarından biridir. 10. sınıf matematik müfredatında yer alan fonksiyon türleri, öğrencilerin fonksiyonları daha derinlemesine anlamalarına yardımcı olur ve ileri matematik konularına temel oluşturur. Bir fonksiyon, iki küme arasındaki her elemanı bir diğer kümeye eşleyen bir ilişkidir. Bu ilişkiler, farklı özelliklere göre sınıflandırılır ve her biri farklı matematiksel problemlerin çözümünde kullanılır.

Bu bölümünde, fonksiyon türlerini tanıtacak ve bu fonksiyonların temel özelliklerini inceleyeceğiz. Fonksiyonların sınıflandırılması, matematiksel problemlerde doğru yaklaşımı seçmek ve problemlerin doğru şekilde çözülmesi açısından büyük önem taşır.

10. SINIF FONKSİYON TÜRLERİ DERS NOTU

1. Bire Bir Fonksiyon

İhsan Bey’in yaşları 15, 19, 25 olan Abdullah, Burak ve Gökhan isimli üç çocuğu olduğunu düşünelim.

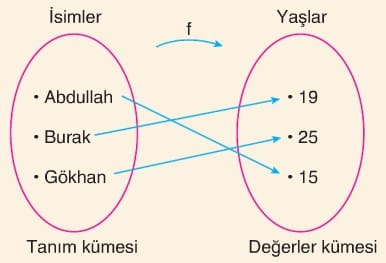
Tanım kümesindeki farklı kişilerin yaşları da farklı olduğu görülmektedir.

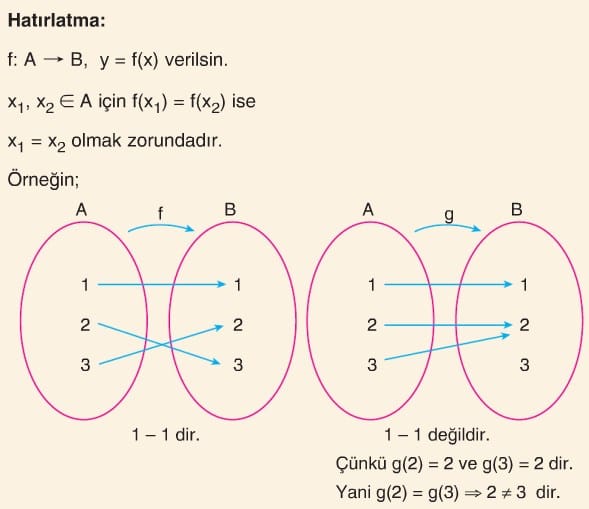
Genel olarak f: A → B, y = f(x) fonksiyonu verilsin. A tanım kümesindeki farklı iki elemanın eğer görüntüleri de farklı oluyorsa f ye bire bir fonksiyon denir. Yani her x₁, x₂ ∈ A için eğer x₁ ≠ x₂ iken f(x₁) ≠ f(x₂) oluyorsa f ye bire bir (1 – 1) fonksiyon denir.

Yatay Doğru Testi

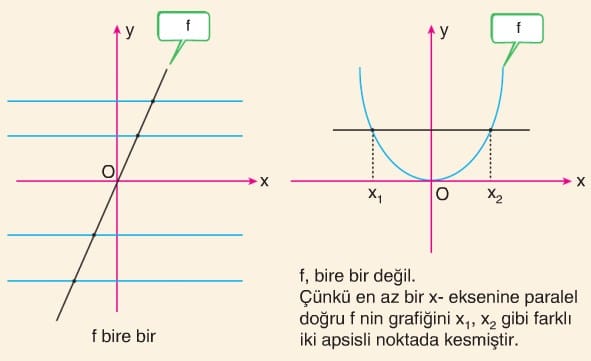
Bir fonksiyonun grafiği verildiğinde (veya fonksiyonun grafiğini biz çizersek) 0 fonksiyonun bire bir olup olmadığını anlamak için fonksiyonun grafiğini kesecek biçimde x- eksenine paralel doğrular çizilir. Eğer bu paralel doğrular verilen grafiği birden çok yerde keserse fonksiyon bire bir olmaz. Grafiği kesen her doğru bir tek noktada keserse fonksiyon 1 – 1 olur.

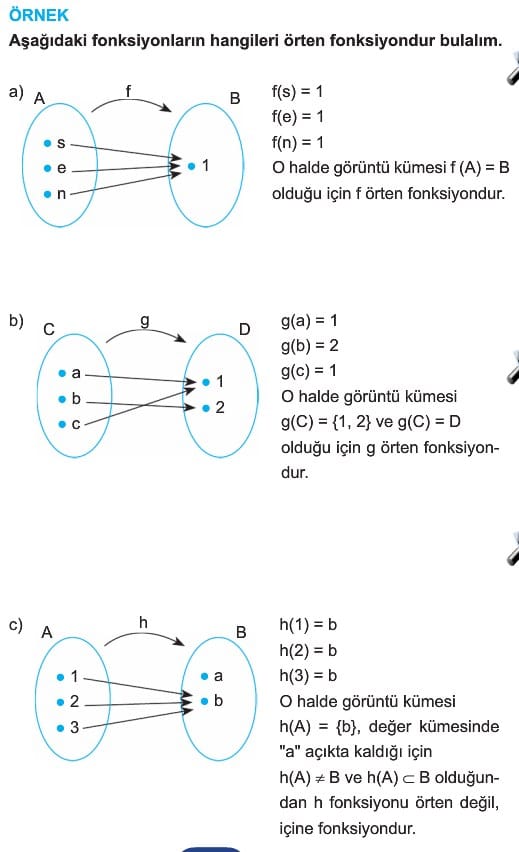
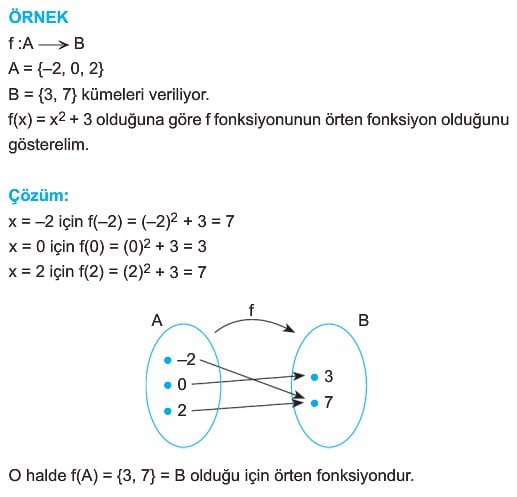
2. Örten Fonksiyon

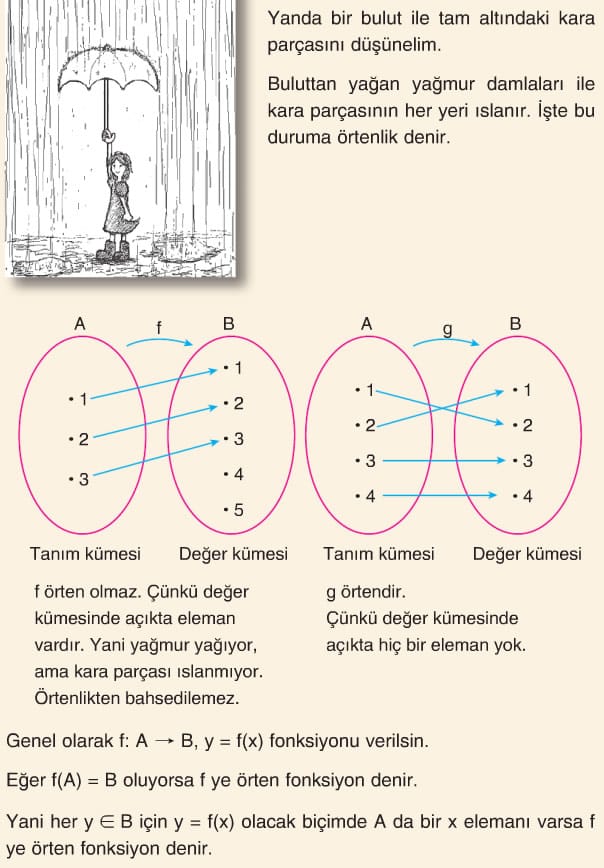
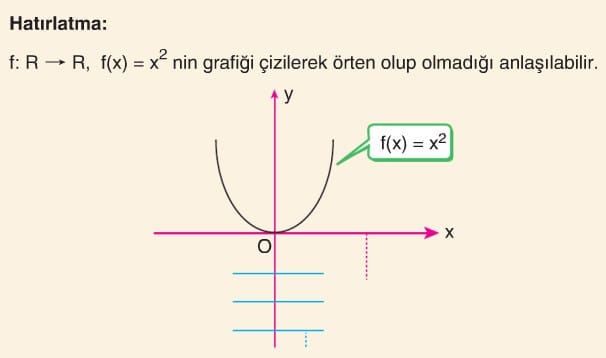
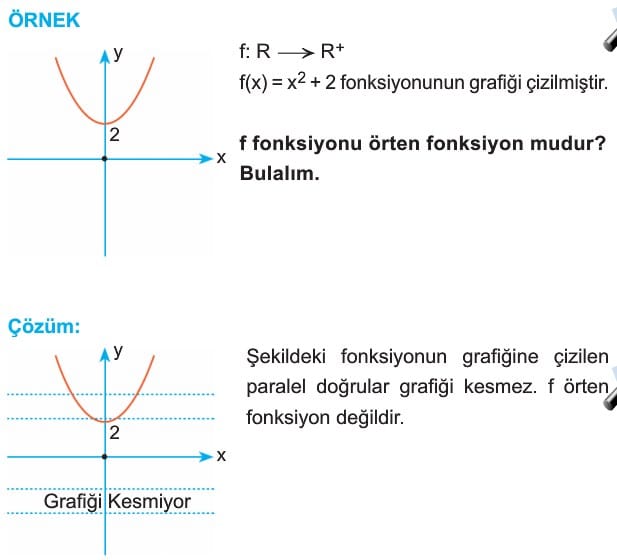
Fonksiyonda değer kümesi R dir. Bu fonksiyonun örten olması için mavi ile gösterilen yerlere karşılık tanım kümesinde kırmızı ile gösterilen yerlerde mutlaka bir x sayısı olmalıdır. Örneğin f(x) = – 2 olan hiçbir reel sayı bulunamaz. Demek ki değerler kümesi tamamen örtülmemiştir. Bunu daha net anlamak için yatay doğru testi yapılabilir. Fonksiyonun görüntü kümesinde olmak kaydıyla x- eksenine çizilen paralel doğrulardan en az bir tanesi grafiği kesmiyor ise fonksiyon örten olamaz.

f: R → R, f(x) : x² fonksiyonunu örten yapabiliriz. Bunun için

f: R → [0, ∞), f(x) = x² biçiminde tanımlanırsa f örten olur.

Örnek:

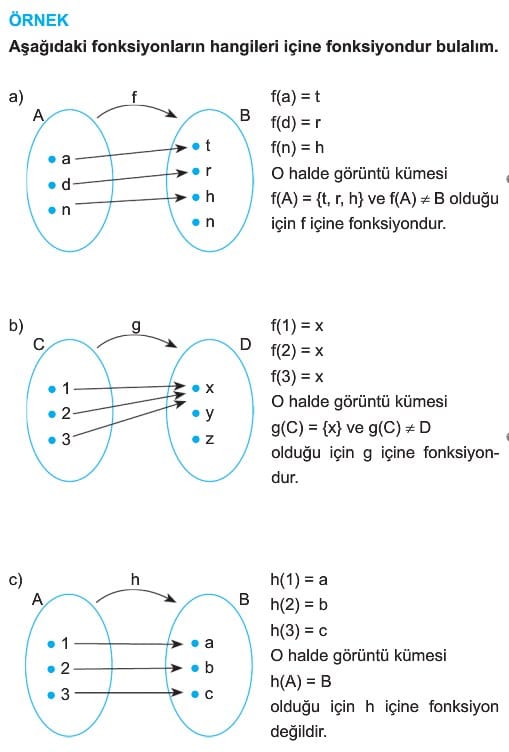
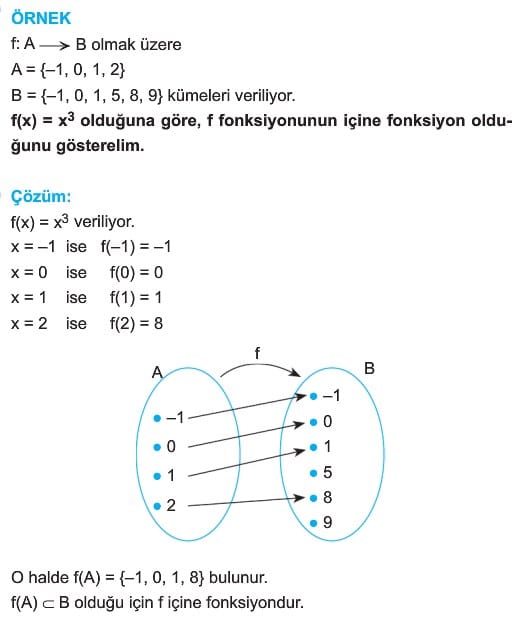
3. İçine Fonksiyon

Örten olmayan fonksiyona içine fonksiyon denir.

4. Sabit Fonksiyon

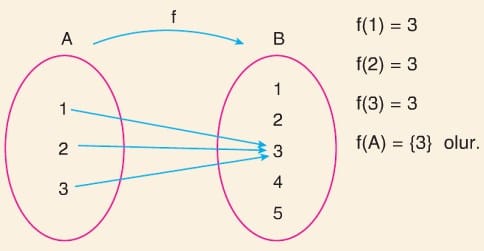
Tanım kümesindeki her eleman değer kümesinde yalnızca bir elemanla eşleşen fonksiyonlara sabit fonksiyon denir. c bir gerçek sayı olmak üzere sabit fonksiyonlar f(x) = c biçiminde gösterilir.

Hatırlatma: y = f(x) = c sabit fonksiyonunda x li terimler olmaz.

Örnek:

5. Birim Fonksiyon

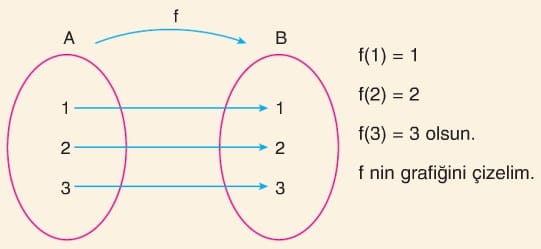
Tanım kümesindeki her elemanı yine kendisine dönüştüren kurala birim fonksiyon denir ve f(x) = x biçiminde gösterilir.

f: R → R, f(x) = x in grafiği çizilirken y = x doğusunu çizmek yeterlidir.

Hatırlatma: y = f(x) = x fonksiyonuna I. açıortay doğrusu denir. f(x) = x birim fonksiyonunda x li terim dışında hiçbir terim olmamalıdır.

Örnek:

6. Doğrusal Fonksiyon

0 ≠ a, b ∈ R verilen sabit sayıları göstermek üzere

f: R → R, f(x) = ax + b biçimindeki fonksiyonlara doğrusal fonksiyon denir.

Hatırlatma: f(x) = ax + b nin grafiğini çizmek demek y = ax + b doğrusunun grafiğini çizmek demektir.

Örnek:

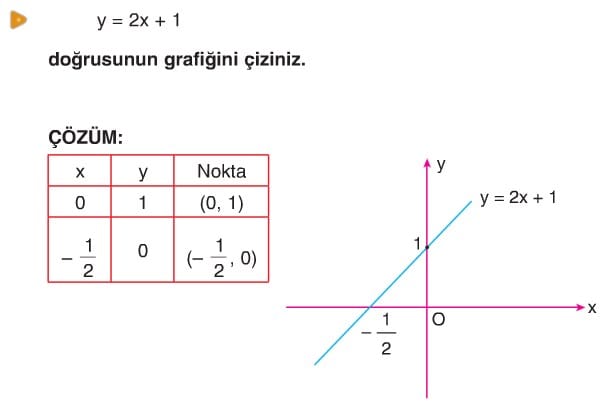
Örnek:

7. Parçalı Tanımlı Fonksiyonlar

Tanım kümesinin belli aralıklarında kuralı değişen fonksiyonlara parçalı tanımlı fonksiyonlar denir.

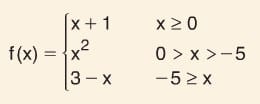
fonksiyonu parçalı tanımlı fonksiyondur. Bu fonksiyonda herhangi bir x değeri için işlem yapılırken x’in hangi aralıkta olduğu bulunarak o aralığa ait kural kullanılır.

Örnek:

8. Eşit Fonksiyonlar

Fonksiyon Türleri Soruları ve Çözümleri

Çözümlü Örnek Test Soruları

Fonksiyon Türleri

Soru 1: f: R → R ve f(x) = 3x + 5 fonksiyonu hangi tür fonksiyondur?
A) Sabit Fonksiyon
B) Doğrusal Fonksiyon
C) Parabolik Fonksiyon
D) Birim Fonksiyon
Cevap: B
Çözüm: f(x) = 3x + 5 doğrusal bir fonksiyondur çünkü fonksiyonun derecesi 1’dir.

Soru 2: g(x) = 4 fonksiyonu aşağıdakilerden hangisidir?
A) Sabit Fonksiyon
B) Doğrusal Fonksiyon
C) Parabolik Fonksiyon
D) Birim Fonksiyon
Cevap: A
Çözüm: g(x) = 4 her x değeri için aynı sonucu verdiğinden sabit bir fonksiyondur.

Soru 3: h(x) = x^2 + 2x + 1 fonksiyonu hangi tür fonksiyondur?
A) Doğrusal Fonksiyon
B) Sabit Fonksiyon
C) Parabolik Fonksiyon
D) Birim Fonksiyon
Cevap: C
Çözüm: h(x) = x^2 + 2x + 1 ifadesinde en yüksek derece 2 olduğundan bu bir parabolik fonksiyondur.

Soru 4: f(x) = x fonksiyonunun adı nedir?
A) Sabit Fonksiyon
B) Doğrusal Fonksiyon
C) Parabolik Fonksiyon
D) Birim Fonksiyon
Cevap: D
Çözüm: f(x) = x fonksiyonuna birim fonksiyon denir çünkü her x değeri için f(x) = x olur.

Soru 5: Hangi tür fonksiyonda görüntü kümesi yalnızca bir elemandan oluşur?
A) Sabit Fonksiyon
B) Doğrusal Fonksiyon
C) Parabolik Fonksiyon
D) Birim Fonksiyon
Cevap: A
Çözüm: Sabit fonksiyonda tüm x değerleri için aynı y değeri çıkar, bu yüzden görüntü kümesi tek bir elemandan oluşur.

Soru 6: f(x) = -3x + 2 fonksiyonu hangi tür fonksiyondur?
A) Sabit Fonksiyon
B) Doğrusal Fonksiyon
C) Parabolik Fonksiyon
D) Birim Fonksiyon
Cevap: B
Çözüm: f(x) = -3x + 2 doğrusal bir fonksiyondur çünkü derecesi 1’dir.

Soru 7: g(x) = 2x^2 – 3x + 1 fonksiyonu hangi tür fonksiyondur?
A) Sabit Fonksiyon
B) Doğrusal Fonksiyon
C) Parabolik Fonksiyon
D) Birim Fonksiyon
Cevap: C
Çözüm: Bu fonksiyonun en yüksek derecesi 2 olduğundan, parabolik fonksiyon olarak sınıflandırılır.

Soru 8: Birim fonksiyon olan f(x) = x için tanım ve görüntü kümeleri arasındaki ilişki nasıldır?
A) Tanım kümesindeki her eleman farklı bir görüntü kümesi elemanına gider
B) Tanım kümesindeki her eleman kendisine gider
C) Tanım kümesindeki her eleman sıfıra gider
D) Tanım kümesi ile görüntü kümesi arasında hiçbir ilişki yoktur
Cevap: B
Çözüm: Birim fonksiyon olan f(x) = x tanım kümesindeki her elemanı kendisine gönderir.

Soru 9: f(x) = k (k sabit bir sayı) şeklindeki fonksiyonlar hangi türdendir?
A) Sabit Fonksiyon
B) Doğrusal Fonksiyon
C) Parabolik Fonksiyon
D) Birim Fonksiyon
Cevap: A
Çözüm: f(x) = k şeklindeki fonksiyonlar sabit fonksiyondur çünkü tüm x değerleri için y aynı çıkar.

Soru 10: Bir fonksiyonun doğrusal olabilmesi için en yüksek dereceli terimin derecesi kaç olmalıdır?
A) 0
B) 1
C) 2
D) 3
Cevap: B
Çözüm: Doğrusal bir fonksiyonda en yüksek terim derecesi 1 olmalıdır; örneğin f(x) = mx + b.

Fonksiyon, matematiksel olarak iki küme arasında bir ilişki tanımlayan bir kuraldır. Bir kümenin her elemanını başka bir kümenin elemanıyla eşleştiren bu ilişkiye fonksiyon denir. Fonksiyonların tanımlı olduğu küme tanım kümesi (domain), ve fonksiyonun sonuçlarının yer aldığı küme değer kümesi (range) olarak adlandırılır.

Fonksiyonlar, farklı özelliklerine göre çeşitli türlere ayrılır. Bu türler, fonksiyonun nasıl davrandığını anlamak ve doğru fonksiyonla doğru matematiksel problemleri çözmek için kullanılır.

1. Birebir Fonksiyon (Injective Function)

Bir fonksiyon, birebir (injektif) ise, tanım kümesindeki her elemanın yalnızca bir sonuç ile eşlemesi ve değer kümesinde her sonucun yalnızca bir öncüle sahip olması gerekir. Yani, farklı girdilerden aynı çıkış elde edilemez. Her eleman bir diğerine benzersiz olarak karşılık gelir.

Özellikleri:

• Farklı girdilerden farklı çıktılar elde edilir.
• Tanım kümesinin her elemanı, yalnızca bir değer kümesindeki elemana eşleşir.
• Grafik üzerinde, yatay doğru testi uygulandığında, doğru grafik ile yalnızca bir noktada kesişir.

2. Örten Fonksiyon (Surjective Function)

Bir fonksiyon, örten (sürjektif) ise, değer kümesindeki her eleman tanım kümesindeki en az bir eleman ile eşleşir. Bu durumda, değer kümesi tamamen kapsanır ve hiçbir eleman dışarıda kalmaz.

Özellikleri:

• Değer kümesinde boşta kalan hiçbir eleman olmaz.
• Her bir sonuç, en az bir girdiden elde edilir.

3. Birebir ve Örten Fonksiyon (Bijektif Function)

Eğer bir fonksiyon hem birebir (injective) hem de örten (surjective) ise, bu fonksiyon birebir ve örten (bijektif) olarak adlandırılır. Bijektif fonksiyonlar, tanım kümesindeki her elemanın değer kümesindeki bir elemanla eşleştiği ve değer kümesindeki her elemanın bir öncüle sahip olduğu fonksiyonlardır.

Özellikleri:

• Tanım kümesinin her elemanı değer kümesinde bir elemanla eşleşir.
• Değer kümesinde dışarıda kalan eleman kalmaz.
• Tersi alınabilen fonksiyonlardır (bijektif fonksiyonların tersi de bir fonksiyondur).

4. Sabit Fonksiyon (Constant Function)

Bir fonksiyon, sabit fonksiyon ise, tanım kümesindeki tüm elemanları değer kümesinde aynı elemana eşler. Yani, girdiler ne olursa olsun sonuç hep aynı olur.

Özellikleri:

• Fonksiyon grafiği yatay bir doğrudur.
• Tüm girdiler için aynı çıktı elde edilir.

5. Doğrusal Fonksiyon

Bir fonksiyon doğrusal fonksiyon ise, fonksiyon grafiği bir doğruyla gösterilir. Doğrusal fonksiyonlar, genel olarak f(x) = ax + b formunda yazılır.

Özellikleri:

• Fonksiyon grafiği düz bir çizgidir.
• Fonksiyonun eğimi sabittir.

Örnek:
f(x) = 4x – 5 bir doğrusal fonksiyondur ve grafiği düz bir doğrudur.

6. Mutlak Değer Fonksiyonu

Bir fonksiyon mutlak değer fonksiyonu ise, her sayıyı pozitif yapar. Yani negatif sayıları da pozitif değerlere dönüştürür.

Özellikleri:

• Grafiği “V” şeklindedir.
• Negatif girdiler pozitif yapılır.

Örnek:
f(x) = |x| fonksiyonu mutlak değer fonksiyonudur.

Fonksiyon türleri, matematiksel problemlerin çözümünde doğru fonksiyonun seçilmesine yardımcı olur. 10. sınıf matematik müfredatında öğrenciler, bu fonksiyonları öğrenerek fonksiyonlar arası farkları anlamaya başlarlar. Birebir, örten, sabit, doğrusal, mutlak değer ve parabolik gibi farklı fonksiyon türlerini anlamak, matematiksel analizlerde doğru işlemler yapmayı sağlar. Fonksiyonların doğru sınıflandırılması, problemlerin çözümünde büyük kolaylık sunar.