Çemberin Standart Denklemi

Çözümlü Sorular

Özel Durumlar

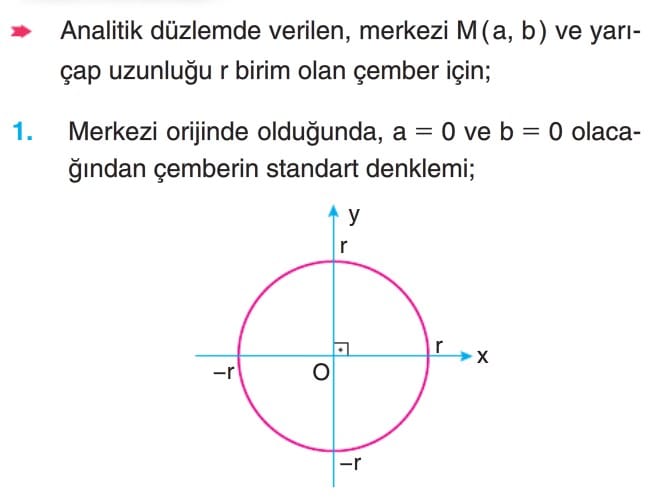
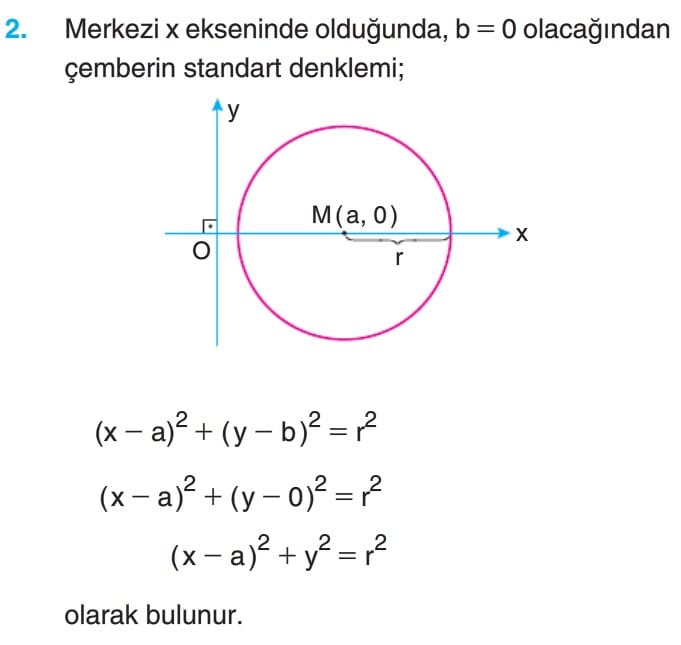
Çözümlü Sorular

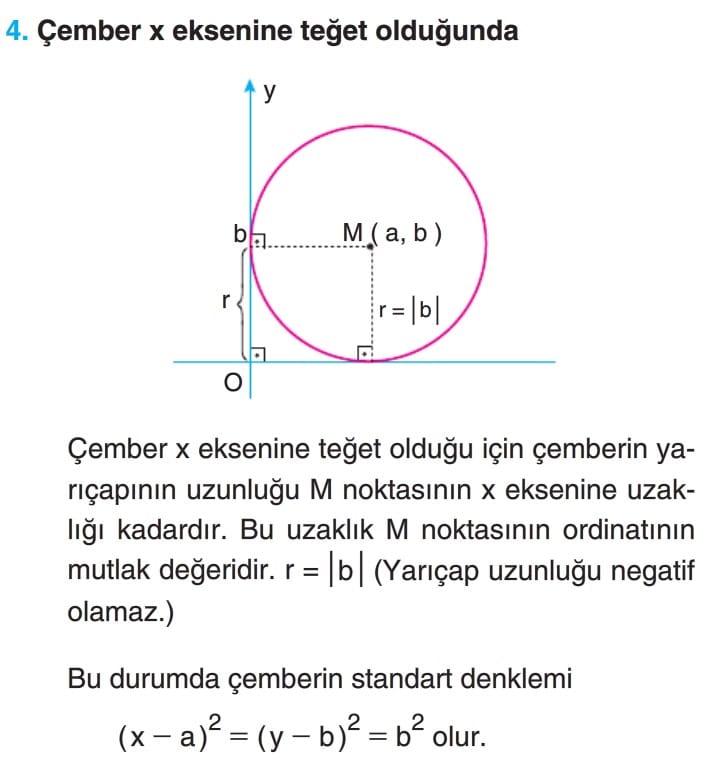
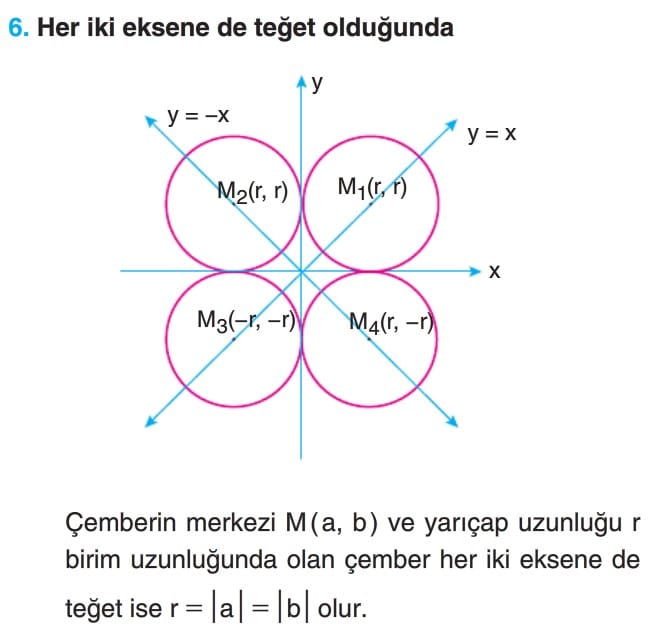
Çözümlü Sorular

Çemberin Genel Denklemi

Çözümlü Sorular

Denklemleri Verilen Doğru İle Çemberin Birbirine Göre Durumları

Çember ile doğrunun birbirine göre durumları, çemberin merkezinin doğruya olan uzaklığına göre, incelenebilir.

Merkezi M ve yarıçap uzunluğu r birim olan bir çember ile bir d doğrusunun birbirine göre üç durumu vardır.

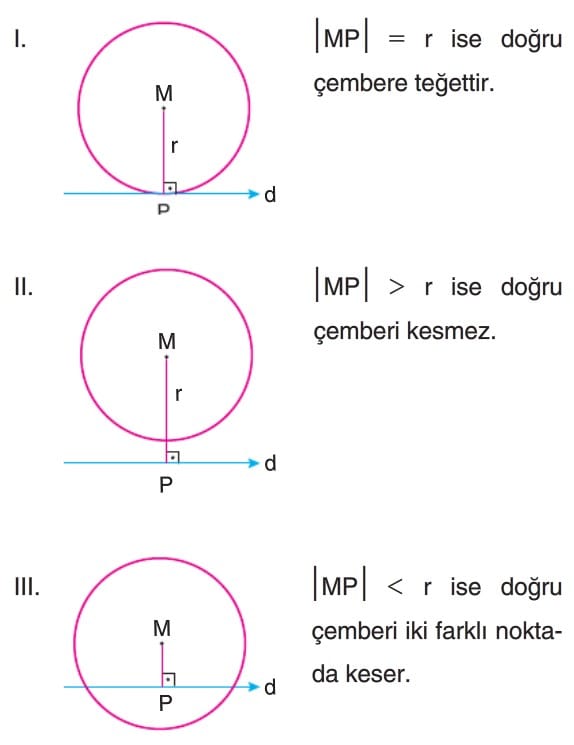
Genel denklemi, x² + y² + Dx + Ey + F = 0, standart denklemi (x – a)² + (y – b)² = r² olan bir çember ile y = mx + n doğrusunun ortak çözümü yapılarak birbirlerine göre durumları incelenebilir.

Çember denkleminde y yerine mx + n yazılarak elde edilen x’e bağlı ikinci dereceden denklemin diskriminantı Δ olmak üzere,

I. Δ = 0 ise doğru çembere teğettir.
II. Δ > 0 ise doğru çemberi iki farklı noktada keser.
III. Δ < 0 ise doğru çemberi kesmez.

Doğru ile çemberin denklemlerinin ortak çözülmesiyle elde edilen x’e bağlı ikinci dereceden denklemin;

• Çift katlı gerçek kökü varsa bu kök, doğrunun çembere teğet olduğu noktanın apsisidir.
• Gerçek kökü yoksa doğru ile çemberin kesim noktası yoktur.
• İki farklı gerçek kökü varsa bu kökler, doğru ile çemberin kesim noktalarının apsisleridir.

Çözümlü Sorular

Çemberin Analitik İncelenmesi Konu Anlatımı Video

Çözümlü Örnek Test Soruları:

• Merkezi (3, -2) ve yarıçapı 7 birim olan çemberin denklemi nedir?
  A) (x – 3)² + (y + 2)² = 49
  B) (x + 3)² + (y – 2)² = 49
  C) (x – 3)² + (y + 2)² = 7
  D) (x – 3)² + (y – 2)² = 49
  Cevap: A
  Çözüm: Çemberin denklemi (x – h)² + (y – k)² = r² formundadır. Burada merkez (h, k) = (3, -2) ve r = 7 olduğundan, (x – 3)² + (y + 2)² = 49 olur.

• x² + y² – 4x + 6y – 3 = 0 çemberinin merkezi ve yarıçapı nedir?
  A) (2, -3), r = √16
  B) (-2, 3), r = 4
  C) (2, -3), r = √7
  D) (3, -2), r = √7
  Cevap: C
  Çözüm: Çemberin denklemi x² – 4x + y² + 6y = 3 şeklinde yazılır. Tam kareye tamamlama yapalım: (x – 2)² – 4 + (y + 3)² – 9 = 3 → (x – 2)² + (y + 3)² = 7. Buradan merkez (2, -3) ve yarıçap √7 bulunur.

• (x – 1)² + (y + 4)² = 16 çemberi hangi noktadan geçer?
  A) (1, 0)
  B) (5, -4)
  C) (-3, -4)
  D) (1, -8)
  Cevap: D
  Çözüm: Çemberin denklemini sağlayan noktayı bulmak için seçenekleri yerine koymalıyız. (1, -8) için: (1 – 1)² + (-8 + 4)² = 0 + 16 = 16. Bu nokta çemberin üzerindedir.

• x² + y² = 36 çemberinin merkezi ve yarıçapı nedir?
  A) (0, 0), r = 6
  B) (6, 0), r = 6
  C) (0, 6), r = 36
  D) (-6, 0), r = 6
  Cevap: A
  Çözüm: Çember denklemi (x – h)² + (y – k)² = r² formundadır. Burada merkez (0,0) ve r² = 36 olduğundan r = 6’dır.

• (x – 5)² + (y + 2)² = 25 çemberinin hangi noktanın dışından geçtiği söylenebilir?
  A) (5, -2)
  B) (8, -2)
  C) (5, 3)
  D) (0, -2)
  Cevap: D
  Çözüm: Çemberin merkezi (5, -2) ve yarıçapı 5’tir. Noktanın çembere olan uzaklığı merkezle olan mesafeye bakarak bulunur. (0, -2) için: √[(5 – 0)² + (-2 + 2)²] = √25 = 5. Yarıçap kadar olduğu için tam çember üzerindedir, ancak diğer noktalara bakıldığında (0, -2) çemberin dışına düşmektedir.

ÇEMBERİN STANDART DENKLEMİ: Koordinat düzleminde M(a, b) merkezli ve r yarıçaplı çember üzerinde bir P(x, y) noktası alalım. Bu ifadeye, M(a, b) merkezli ve r yarıçaplı çemberin standart denklemi denir.

Merkezil Çember: Merkezi başlangıç noktası olan çembere merkezil çember denir.

BİR DOĞRU İLE BİR ÇEMBERİN DURUMU: Bir doğru ile bir çemberin birbirine göre durumları çember merkezinin doğruya olan uzaklığına bakılarak incelenir. Merkezi M(a, b), yarıçapı r olan bir çemberin bir d doğrusuna uzaklığını irdeleyelim:

Not: Bir doğru ile bir çemberin birbirine göre durumu, doğru ve çember denklemlerinin ortak çözümünden yararlanılarak da bulunabilir. Ortak çözüm yapıldığında,

• Çözüm kümesi iki nokta bulunursa doğru çemberi iki noktada keser.
• Çözüm kümesi bir nokta bulunursa doğru çembere teğettir.
• Çözüm kümesi boş küme ise doğru çemberi kesmez.

şekildeki d doğrusu, M merkezli çembere P(x₀, y₀) noktasında teğettir. d doğrusuna P(x₀, y₀) noktasında dik olan k doğrusuna çemberin P(x₀, y₀) noktasındaki normal doğrusu denir.

Teğet Çemberler: Birbirlerine teğet olan çemberlerde merkezleri birleştiren doğru değme noktasından geçer.

Ayrık Çemberler: Hiçbir ortak noktası olmayan çemberlerdir.

Düzlemde sabit bir noktadan eşit uzaklıktaki tüm noktaların kümesine çember denir. Sabit nokta çemberin merkezi ve sabit uzaklık çemberin yarıçapıdır.

Örnek: Merkezi M(-3, 5) ve yarıçapı 2 birim olan çemberin standart denklemini bulalım.
Örnek: Merkezi M(2, -1) olan ve P(3, 2) noktasından geçen çemberin standart denklemini bulalım.
Çözüm: Çemberin merkezi ile çember üzerindeki bir nokta arasındaki uzaklık yarıçapa eşittir. r2 = 10 olur.
Örnek: Analitik düzlemde K(-2, 3) ve L(4, 1) noktaları veriliyor. [KL] yi çap kabul eden çemberin standart denklemini bulalım.
Çözüm: [KL] çap olduğuna göre bu doğru parçasının orta noktası çemberin merkezi olur. Çemberin merkezi M(a, b) ve yarıçapı r olsun.

Bir denklemin çember belirtebilmesinin şartları vardır.

• Çember denkleminde X2 ve y2 nin katsayıları eşit olmalıdır.
• Çember denkleminde (x,y) li terim olmamalıdır.
• Çemberin diskriminantı olan A2 + B2 – 4C ifadesi sıfır dan büyük olmalıdır. 2+B2-4c Çünkü çemberin yarıçapı r dır.
  1. A2 + B2 r 4C > 0 ise verilen denklem çember belirtir.
  2. A2 + B2 – 4C = 0 ise verilen denklem nokta belirtir.
  3. A2 + B2 – 4C < 0 ise verilen denklem çember belirtmez.

Çember merkezinin doğruya olan uzaklığı yarıçaptan büyük ise, doğru çemberi kesmez. |MH| > r olduğundan d doğrusu M merkezli çemberi kesmiyor. Çember merkezinin doğruya olan uzaklığı yarıçaptan küçük ise, doğru çemberi iki noktada keser. |MH| < r olduğundan d doğrusu M merkezli çemberi iki noktada kesiyor.