Üçgende Alan konu anlatımını bitirdikten sonra Üçgende Alan ile ilgili online testler çözebilirsiniz. Aşağıdaki bağlantıya tıklayarak testleri görebilirsiniz.
9. Sınıf Üçgende Alan Online Testler ve Çözümlü Sorular

Üçgenin Alanı

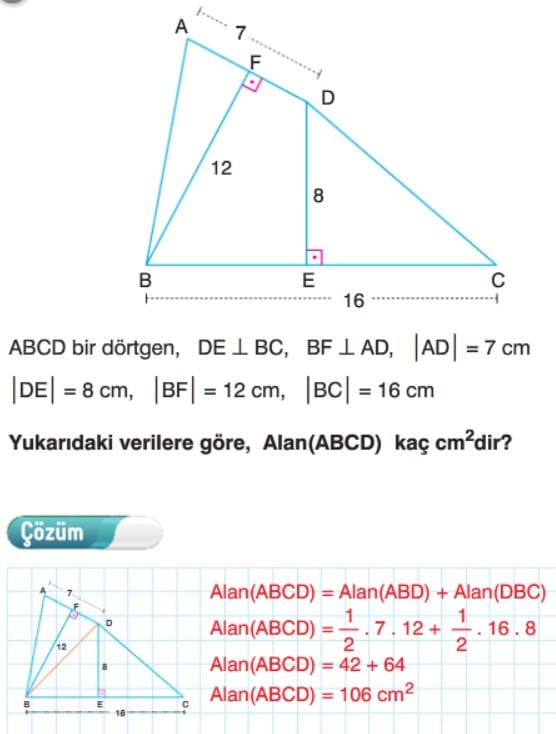
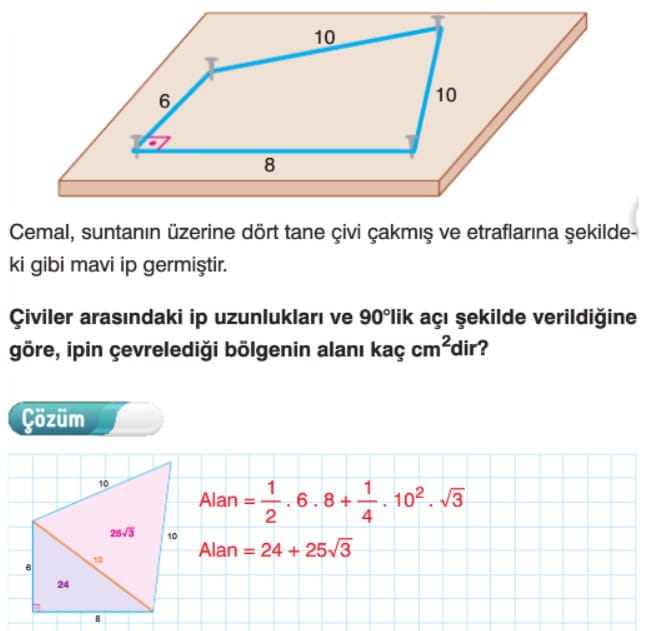
Örnek: 

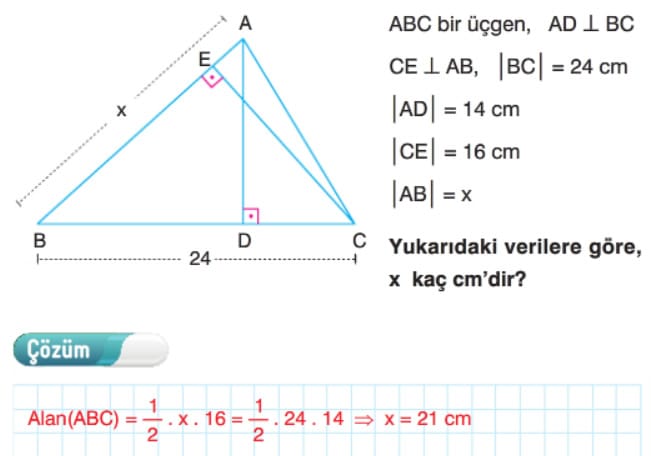
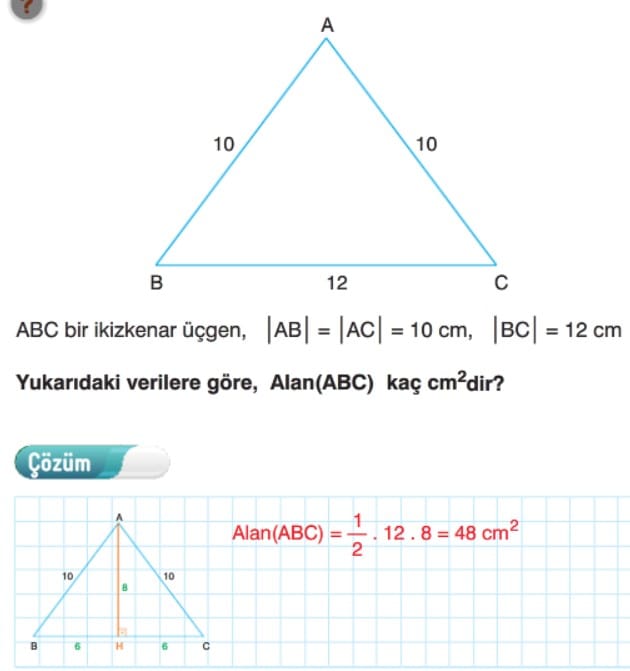
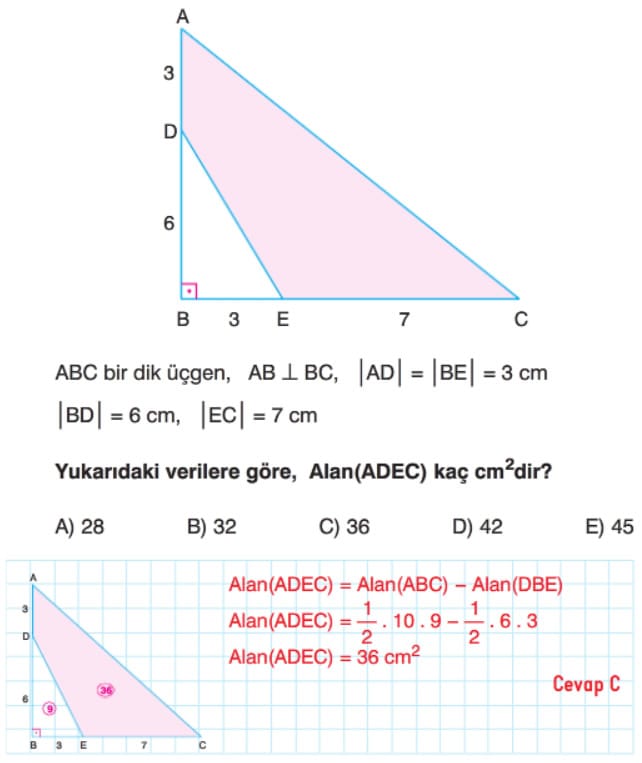
Örnek: 

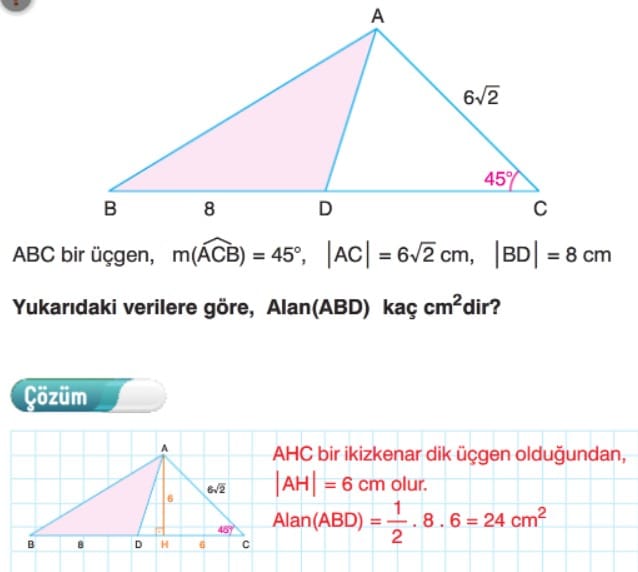
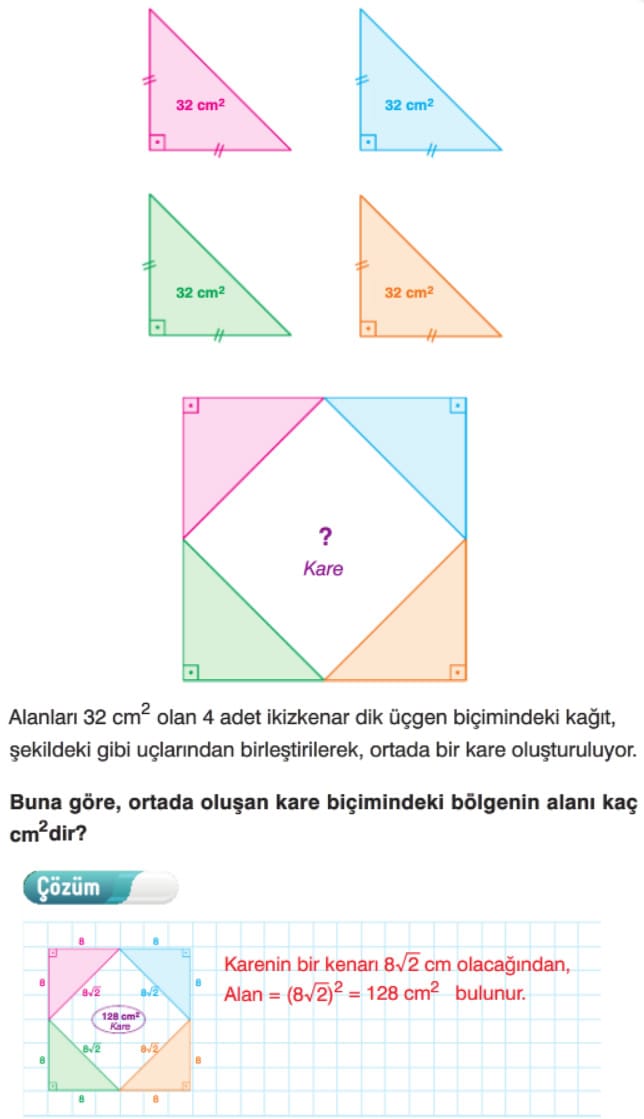
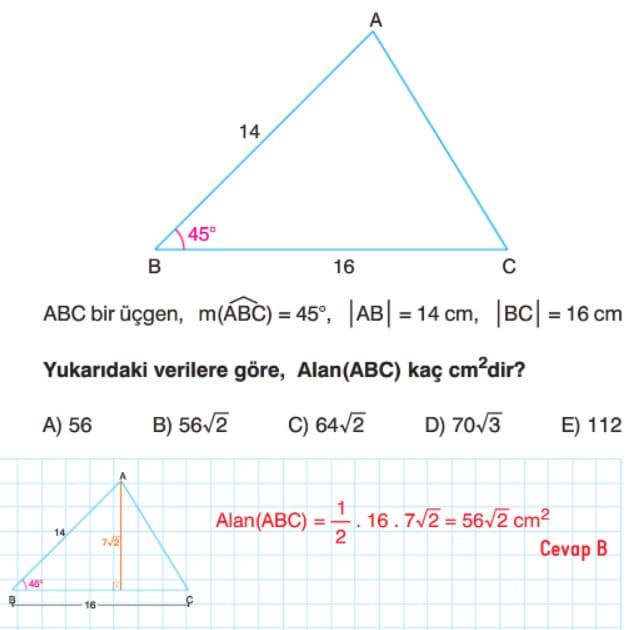
Örnek: 

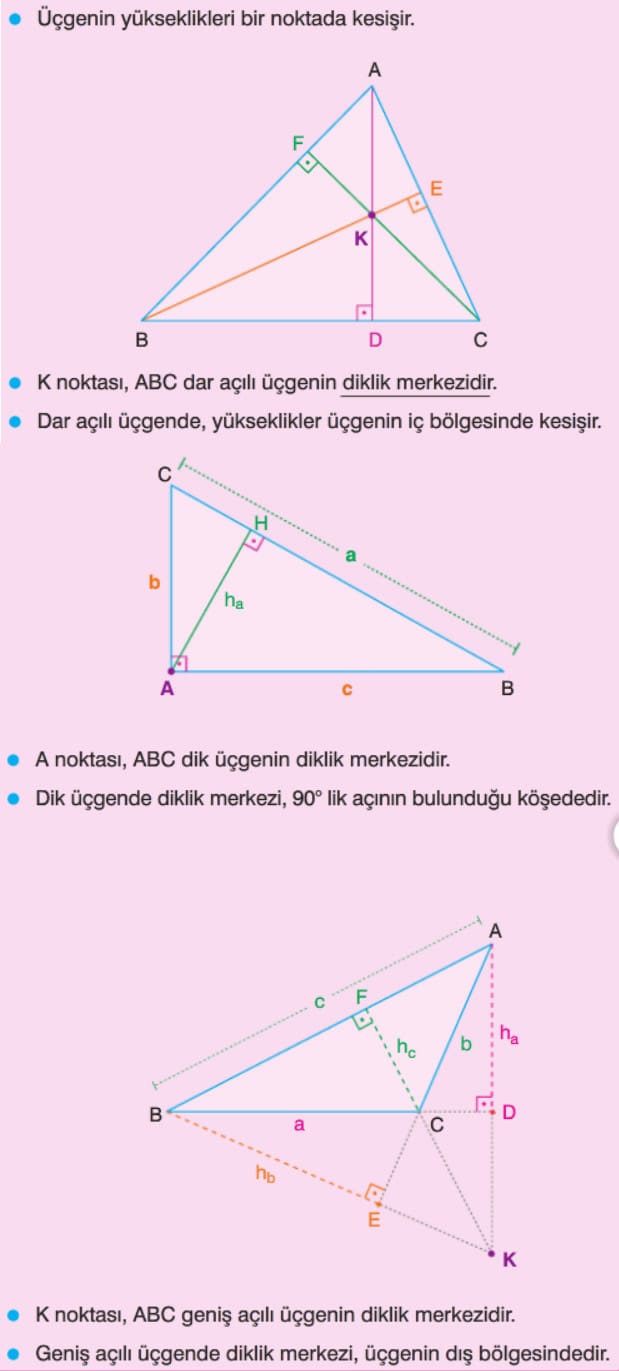
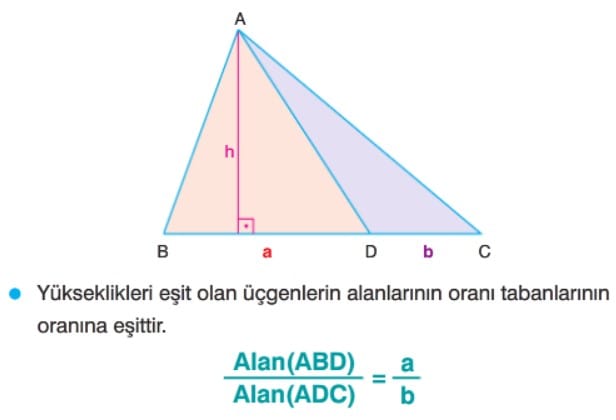
Yükseklikleri Eşit Üçgenler

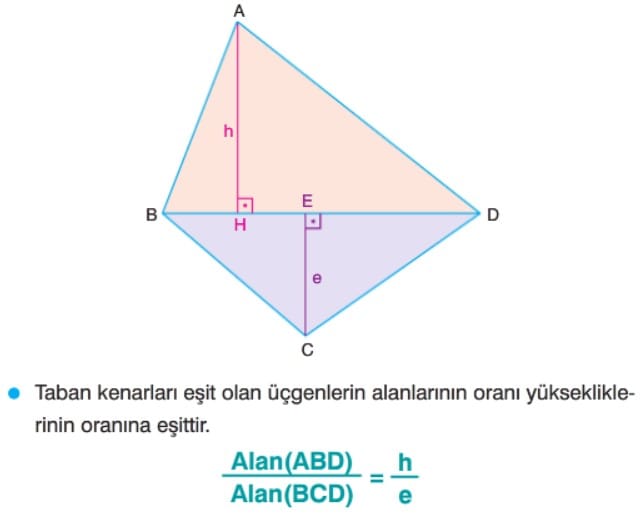
Tabanları Eşit Üçgenler

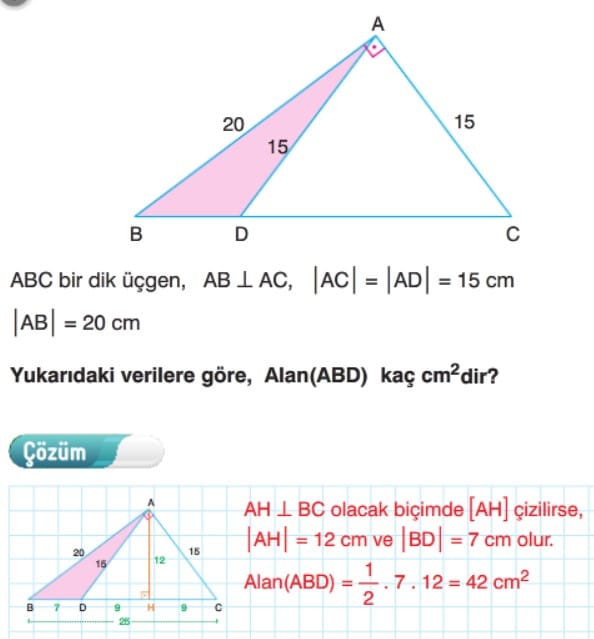
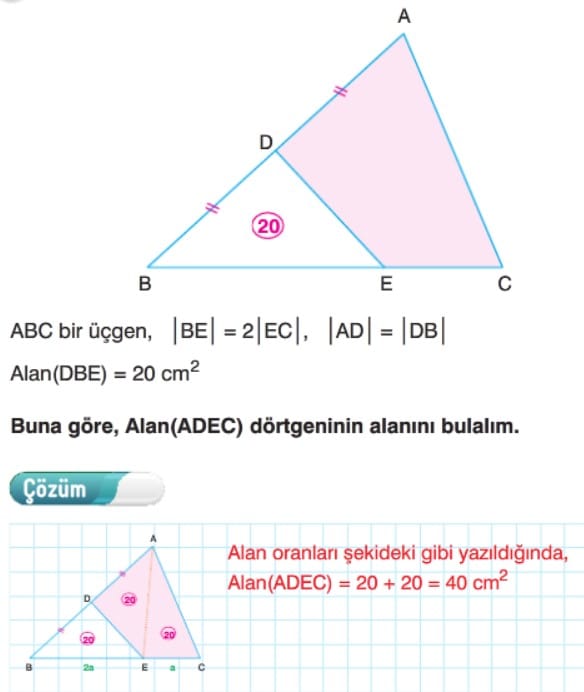
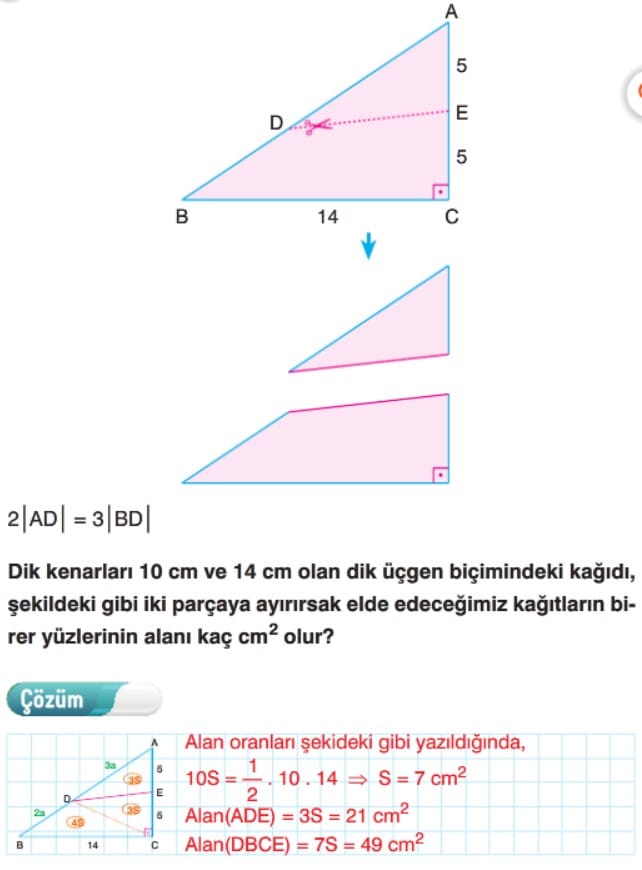
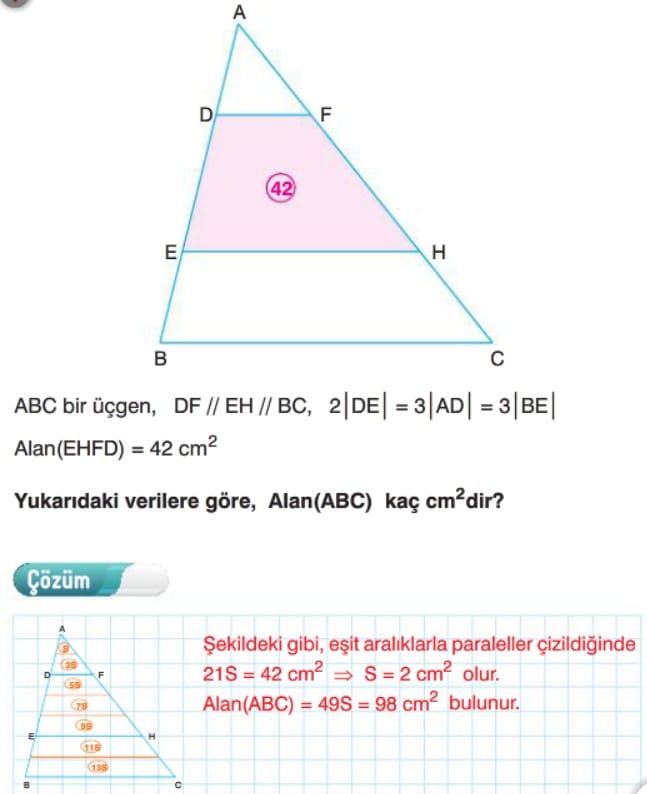
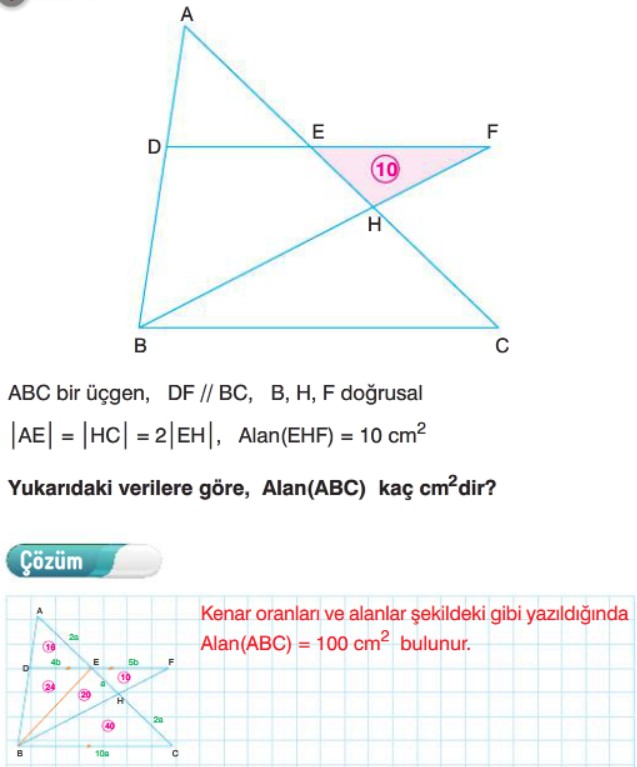
Örnek: 

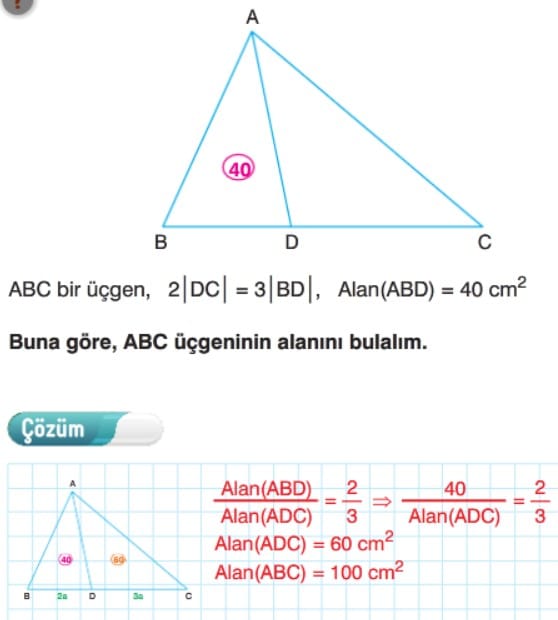
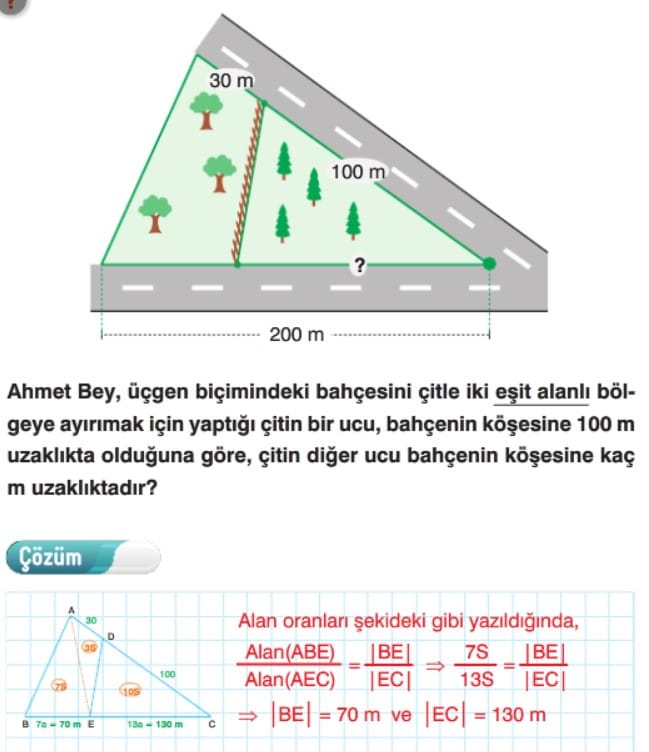
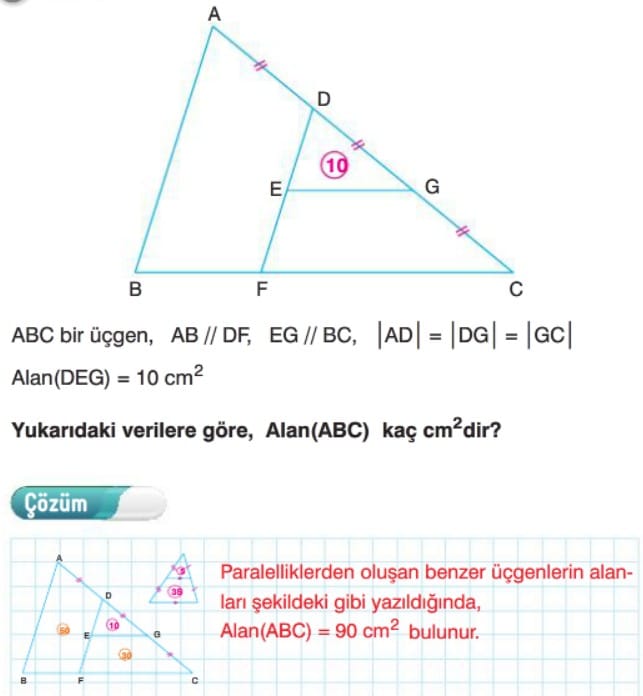
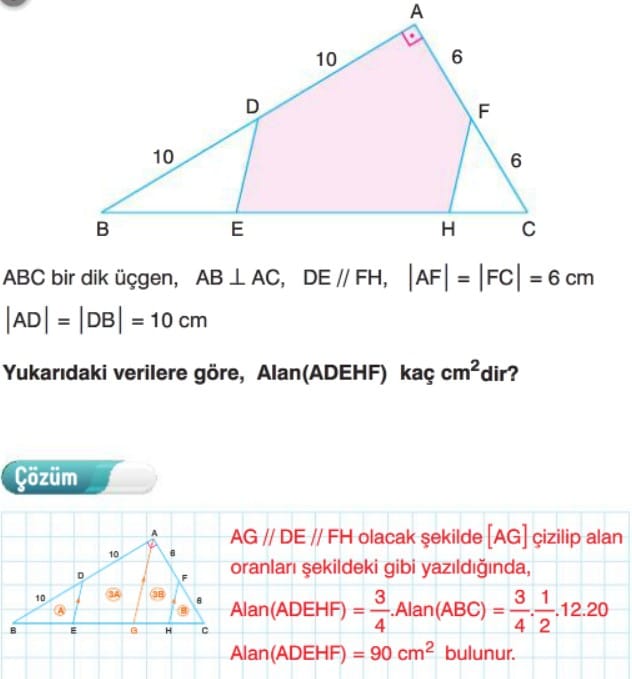
Örnek: 

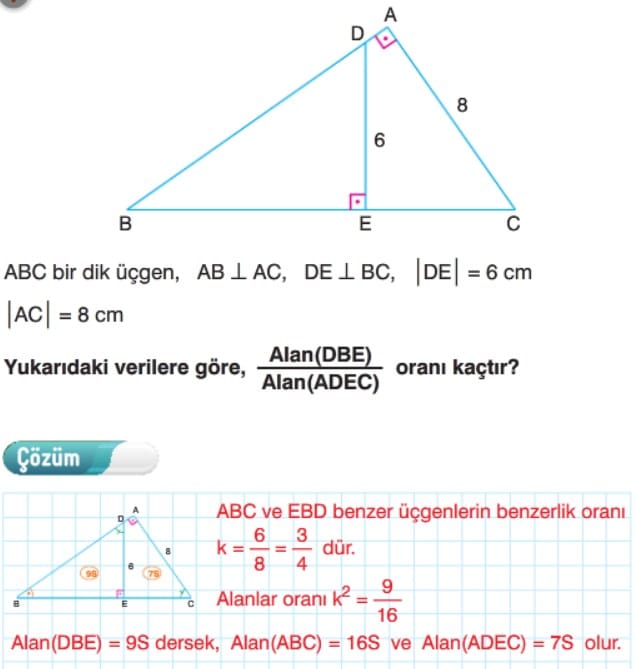
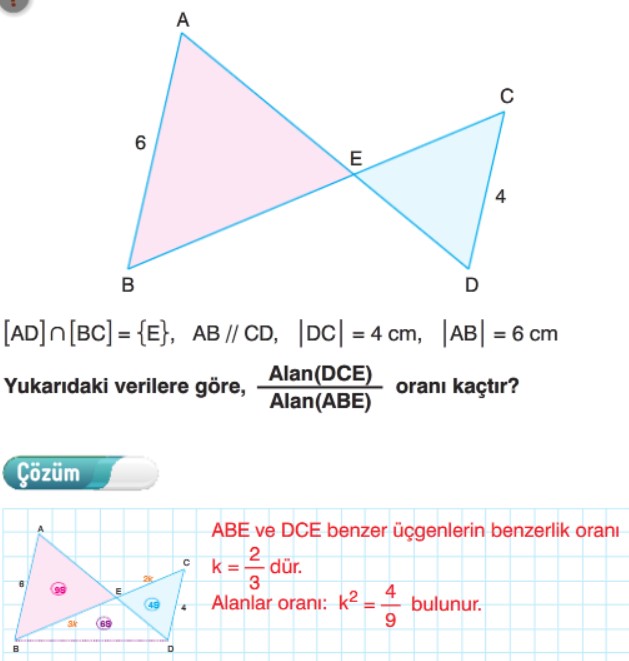
Benzer Üçgenlerin Alanları Oranı

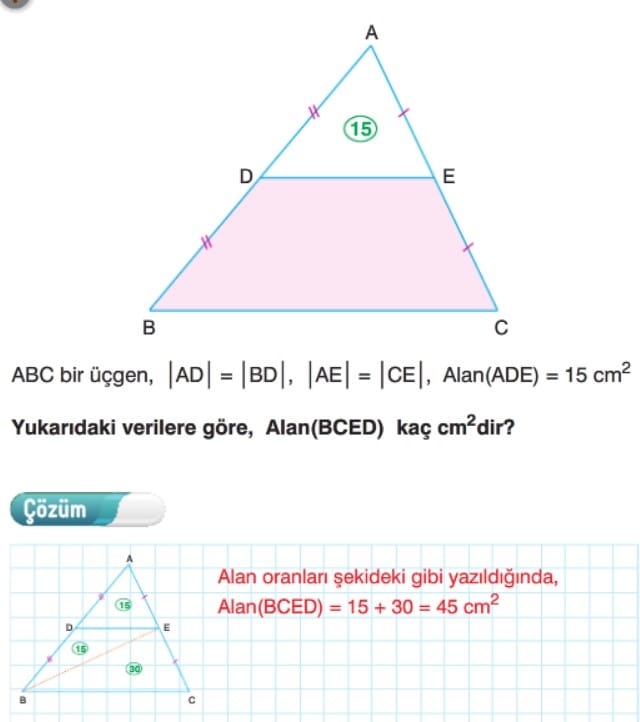
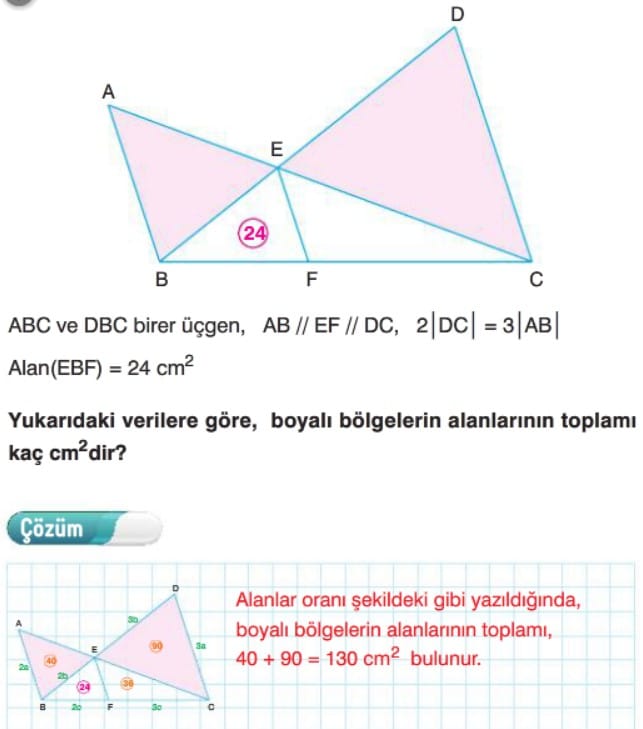
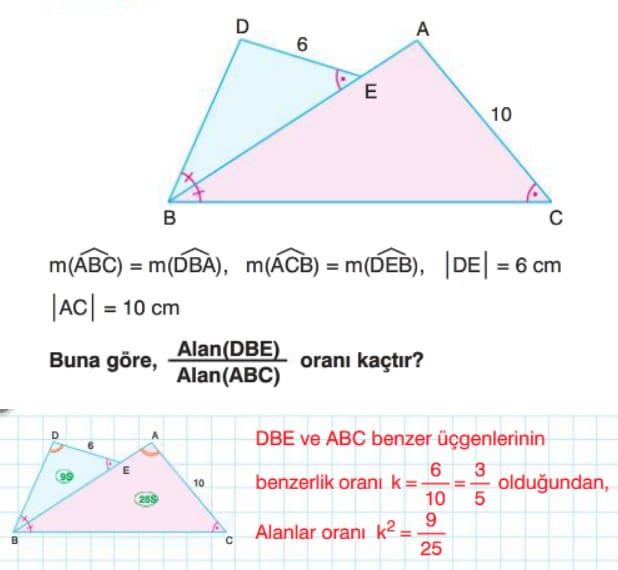
Örnek: 

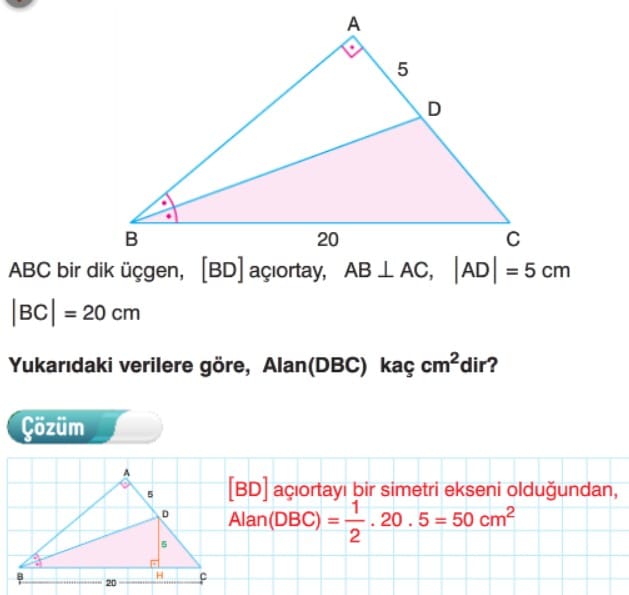
Örnek: 

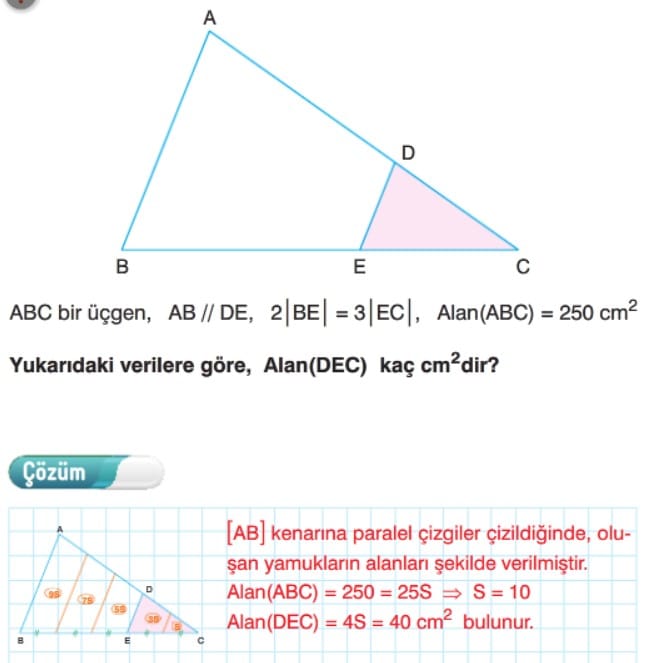
Üçgende Alan Çözümlü Sorular

9. Sınıf Üçgende Alan Online Testler ve Çözümlü Sorular

Çözümlü Örnek Test Soruları: Üçgende Alan

1. Bir üçgenin alanını hesaplamak için aşağıdaki formüllerden hangisi doğrudur?
A) Taban × Yükseklik
B) (Taban × Yükseklik) ÷ 2
C) (Taban × Yükseklik) ÷ 3
D) Taban + Yükseklik
Çözüm:
Bir üçgenin alanı, taban uzunluğu ile o tabana ait yüksekliğin çarpımının yarısı olarak hesaplanır: Alan = (Taban × Yükseklik) ÷ 2.
Doğru cevap: B

2. Taban uzunluğu 8 cm ve yüksekliği 6 cm olan bir üçgenin alanı kaç santimetrekaredir?
A) 24
B) 30
C) 36
D) 48
Çözüm:
Alan = (Taban × Yükseklik) ÷ 2 formülünden, Alan = (8 × 6) ÷ 2 = 48 ÷ 2 = 24 cm² bulunur.
Doğru cevap: A

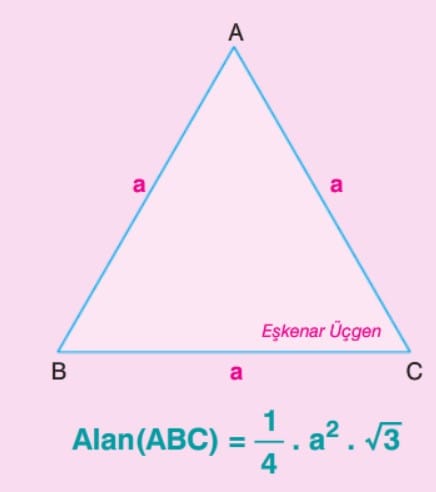
3. Eşkenar bir üçgende bir kenar uzunluğu 10 cm ise, alanını hesaplamak için hangi yöntem kullanılabilir?
A) Taban × Yükseklik ÷ 2
B) Pisagor Teoremi ile yükseklik bulunur ve alan hesaplanır
C) Kenar uzunluklarının toplamı alınır
D) Taban ve yükseklik toplanır
Çözüm:
Eşkenar üçgende yükseklik Pisagor Teoremi ile bulunur. Ardından, Alan = (Taban × Yükseklik) ÷ 2 formülü kullanılır.
Doğru cevap: B

4. Bir üçgenin tabanı 12 cm ve alanı 36 cm² ise, bu üçgenin yüksekliği kaç cm’dir?
A) 5
B) 6
C) 7
D) 8
Çözüm:
Alan = (Taban × Yükseklik) ÷ 2 formülünden, 36 = (12 × Yükseklik) ÷ 2.
36 × 2 = 12 × Yükseklik → 72 = 12 × Yükseklik → Yükseklik = 72 ÷ 12 = 6 cm bulunur.
Doğru cevap: B

5. 9 cm, 12 cm ve 15 cm kenar uzunluklarına sahip bir üçgenin alanını hesaplamak için hangi yöntem kullanılır?
A) Taban × Yükseklik ÷ 2
B) Kenar uzunluklarının toplamı alınır
C) Heron Formülü kullanılır
D) Yüksekliği ölçmek gerekir
Çözüm:
Bu üçgenin yükseklik bilgisi verilmediği için Heron Formülü kullanılır:
Alan = √[s(s-a)(s-b)(s-c)], burada s = (a+b+c)/2 yarı çevredir.
Doğru cevap: C

6. Kenar uzunlukları 6 cm, 8 cm ve 10 cm olan bir üçgenin alanı kaç cm²’dir?
A) 12
B) 24
C) 30
D) 48
Çözüm:
Bu bir dik üçgendir (6² + 8² = 10²). Alan, dik kenarların çarpımının yarısıdır:
Alan = (6 × 8) ÷ 2 = 48 ÷ 2 = 24 cm² bulunur.
Doğru cevap: B

Geometride açı, uzunluk, alan ve hacim hesaplamaları olduğunu düşünürsek, düzlemsel yüzeylerin alanını bulma önemli bir konu başlığıdır. Alan hesaplamalarının temelini üçgende alan konuları oluşturur. Üçgende alanın temelinde de taban ve yükseklik kavramları vardır. Burada öğrendiğiniz bilgileri dörtgen, çokgen ve katı cisimlerin alan hesaplarında da kullanacaksınız.

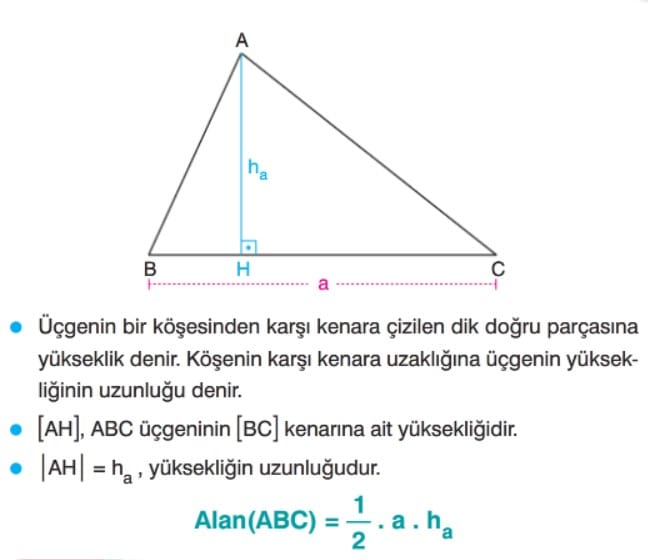
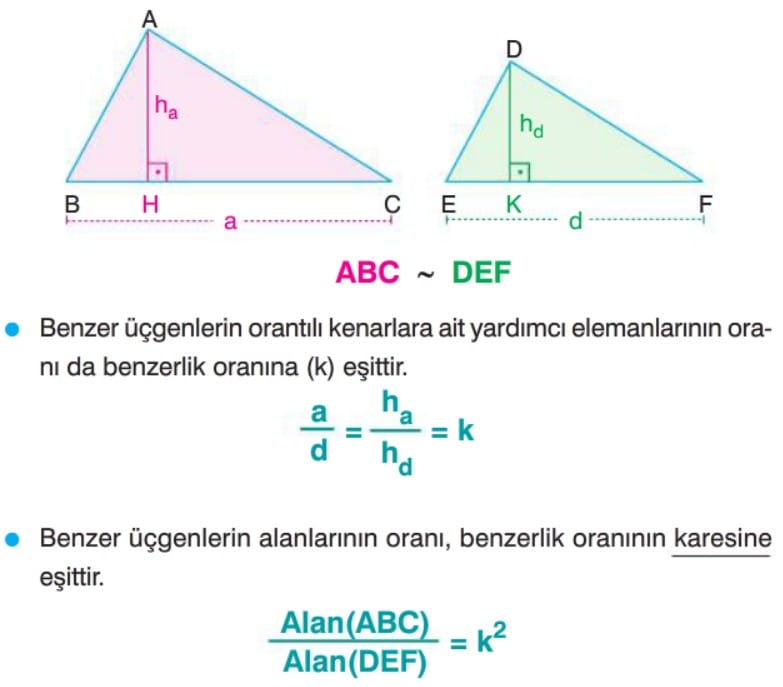
Taban ve Yükseklik ile Alan: Üçgenin bir kenarına karşı köşeden inilen dikmeye 0 kenara ait yükseklik denir. Bir üçgenin alanı herhangi bir kenarı ile bu kenara ait yüksekliğin çarpımının yarısına eşittir.

Üçgenin alanı herhangi bir kenarı ile 0 kenara ait yüksekliğin çarpımının yarısına eşit olduğundan, alan formülünde aşağıdaki b ve c kenarları da taban olarak kullanılabilir.
Dik Üçgenin Alanı: Yandaki dikdörtgen, birim karelerden oluşmuştur. Alt sırada beş tane, üst üste üç tane birim kare olduğundan, şekilde, 5 . 3 = 15 birim kare vardır. Birim karelerden birinin alanı 1 br2 olduğundan, dikdörtgenin alanı 15 br2 dir. Dikdörtgenin alanı, iki kenar uzunluğunun (en ve boy) çarpımı ile bulunur. Bir dikdörtgende köşegen, dikdörtgeni alanları eşit iki tane dik üçgene ayırır. Şekildeki ABD dik üçgeninin alanı;
A(ABD) = a . b olur. Dik üçgenin alanı, dik kenarlarının çarpımının yarısına eşittir. Geniş açılı üçgende, geniş açının kenarlarına ait yükseklikler kenarın uzantısına çizilir ve üçgenin dış bölgesinde olur. Üçgenin bir kenarortayı,
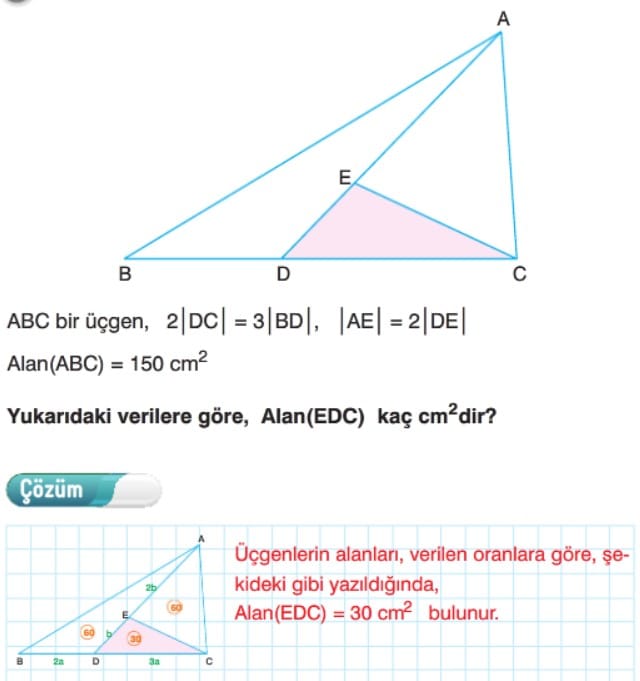
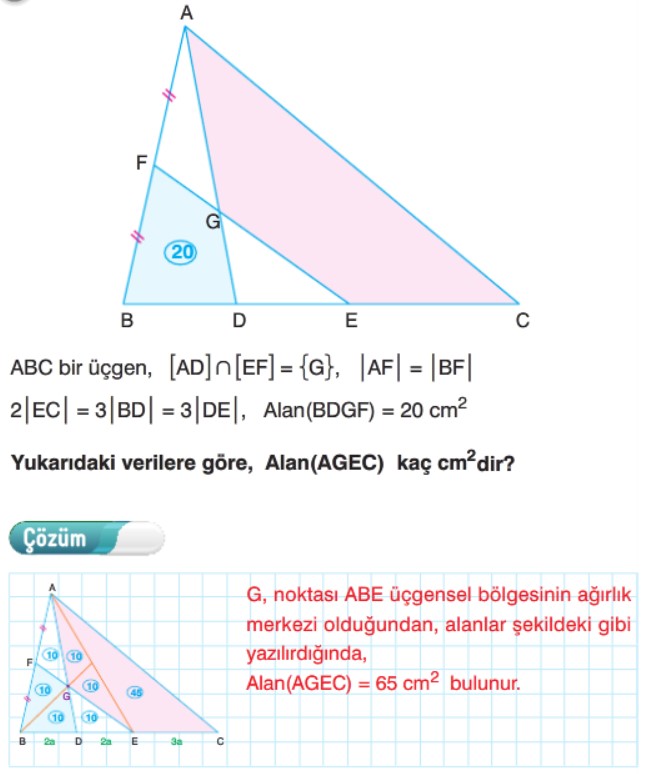
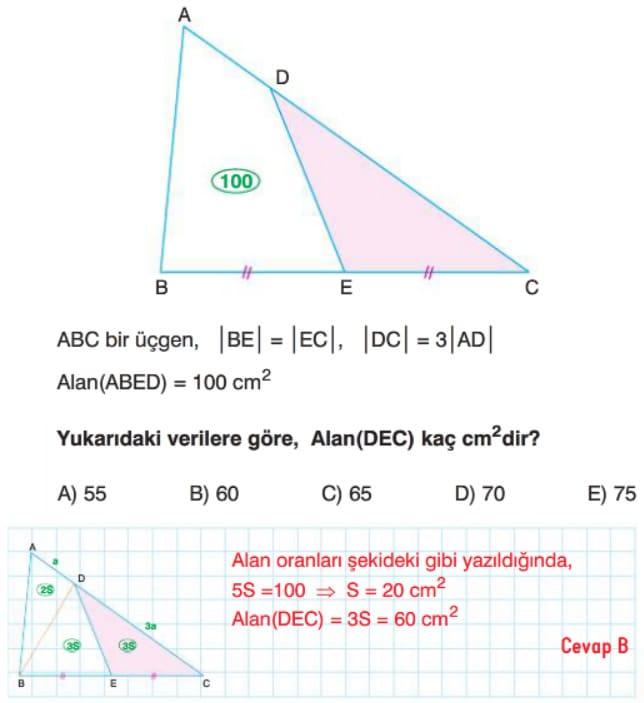
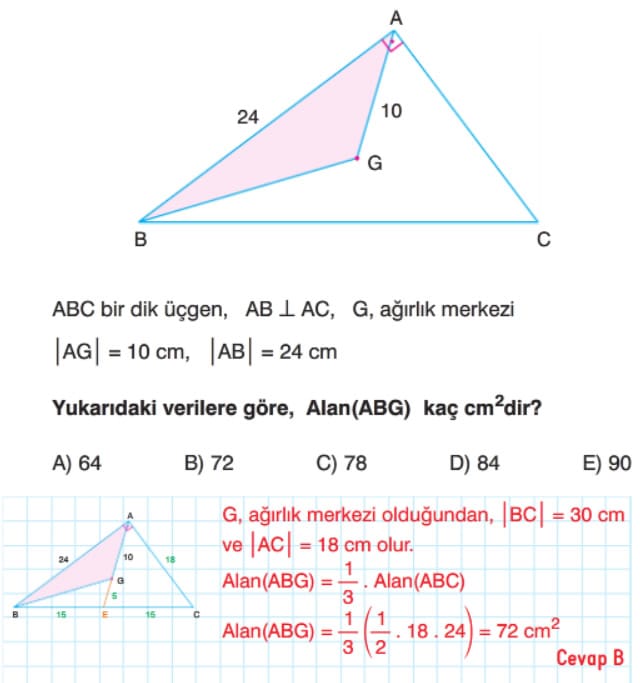
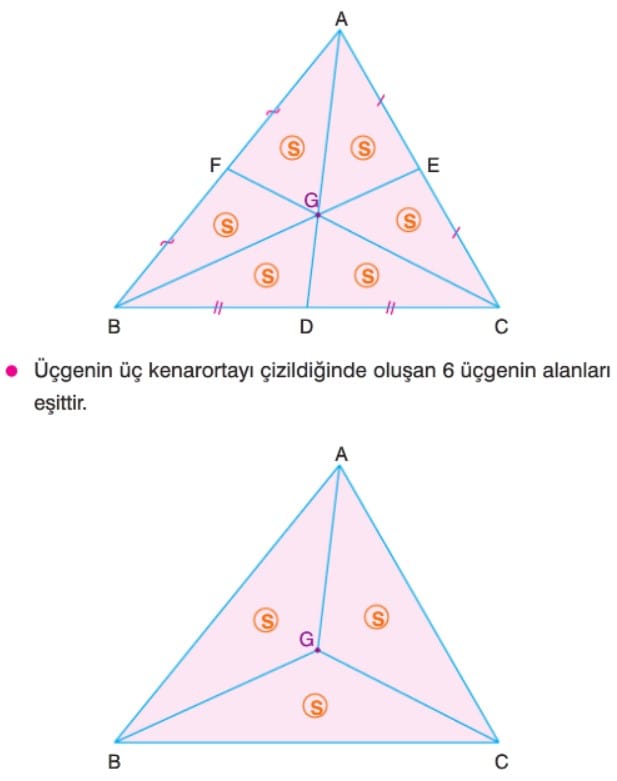
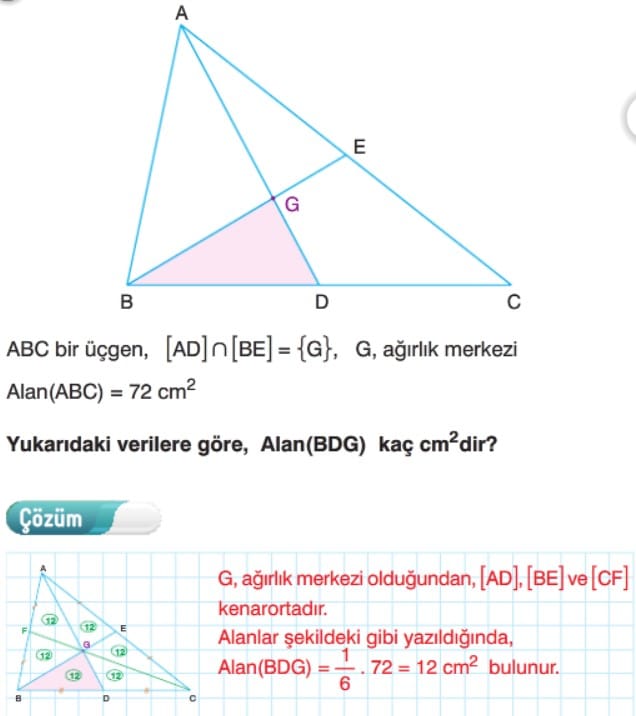
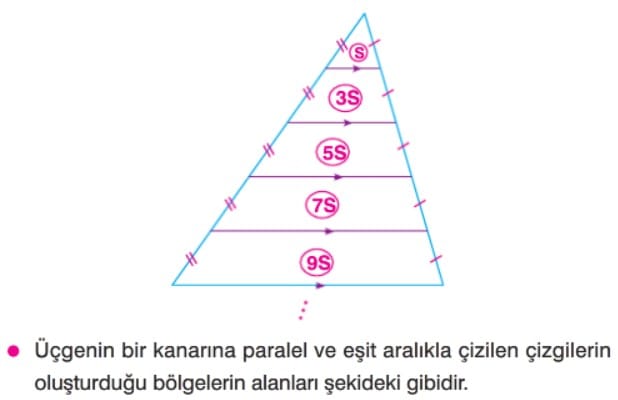
üçgeni alanları eşit iki üçgene ayırır. Kenarortayların kesiştiği nokta ağırlık merkezidir. Ağırlık merkezi kenarortayı 2 ye 1 oranında böler. Yükseklikleri eşit olan üçgenlerin tabanları oranı alanları oranına eşittir. Üç kenarortay, üçgenin alanını 6 eş parçaya ayırır. Ağırlık merkezi köşelere birleştirilirse alanları eşit 3 üçgen oluşur. Şekildeki gibi bir üçgenin iki kenarı paralel doğrularla eşit bölmelere ayrıldığında, bu bölmelerin alanları 1, 3, 5, 7, 9 ardışık tek sayılarıyla orantılı olur.
Çözüm 20: Ağırlık merkezi kenarortayı 2 ye 1 oranında böldüğünden, ağırlık merkezinden geçen tabana paralel doğru da kenarları 2 ye 1 oranında böler. |DB| = kdersek, |AD| = 2k olur. |AL| = |LD| = k olacak şekilde [LN] paralelini çizelim. Kenarlar eşit olduğundan, bölgelerin alanları S, 3S ve 5S olur. S + 3S + 5S = 63 verildiğinden,
9S = 63 ve S = 7 cm2 olur. A(BCED) = 5 . 7 = 35 cm2 bulunur.

Üçgenin alanı hesaplanırken, genellikle iki temel yöntem kullanılır: üçgenin tabanının uzunluğu ile yüksekliğini çarpma ve üçgenin kenar uzunlukları kullanılarak yarı çevresini bulup, bu yarı çevre ile kenar uzunlukları arasındaki ilişkiyi kullanma. İki yöntemi de aşağıda daha detaylı bir şekilde bulabilirsiniz.

Üçgenin Tabanı ve Yüksekliği ile Alan Hesaplama: Üçgenin alanını hesaplamanın en temel yöntemlerinden biri, taban uzunluğunu ve buna dik çizilen yüksekliği kullanmaktır.
Alan Formülü: A = 1/2 x Taban x Taban Yüksekliği
Bu formülde:

• A, üçgenin alanını temsil eder.
• “Taban Uzunluğu”, üçgenin tabanının uzunluğunu ifade eder.
• “Yükseklik”, tabana dik çizilen yüksekliği temsil eder.

Üçgenlerin Tarihçesi:

Üçgenlerle ilgili geometrik çalışmalar, antik çağlara dayanır. Antik Yunan matematikçisi Euclid, “Öklidyen Geometri” adlı eserinde üçgenlerle ilgili birçok teoremi ortaya koymuştur. Ayrıca, trigonometri alanındaki çalışmalar da üçgenlerin anlaşılması ve kullanılması üzerine kurulmuştur.