Standart sapma, verilerin ortalama etrafında nasıl bir yayılma gösterdiğinin ölçüsüdür. Düşük standart sapma değeri, bir araya toplanmış ve ortalamaya daha yakın verilerin çok olduğunun ölçüsüdür.

Bir veri grubundaki her bir sayının aritmetik ortalamadan ne kadar uzaklaştığı standart sapma ile bulunur.

• Grup içindeki farklılaşmaya standart sapma denir ve S ile gösterilir.

• Standart sapma bulunurken aşağıdaki adımlar izlenir:

1. Adım: Veri grubunun aritmetik ortalaması bulunur.

2. Adım: Her verinin aritmetik ortalama ile farkının karesi alınır.

3. Adım: Bulunan toplam, veri sayısının bir eksiğine bölünüp karekökü alınır.

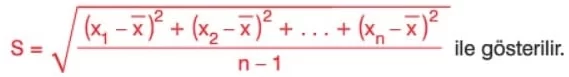
• Standart sapma veri grubundaki elemanların aritmetik ortalamaya yakınlığını ya da uzaklığını verir.
• Standart sapma büyük ise veriler aritmetik ortalamadan uzak küçük ise veriler aritmetik ortalamaya yakındır.
• Standart sapmanın küçük olması grubun homojen, büyük olması grubun heterojen olduğunu gösterir.

 

Örnek: 1, 7, 8, 9, 10, 13, 50 veri grubunun standart sapmasını bulalım.

Çözüm:

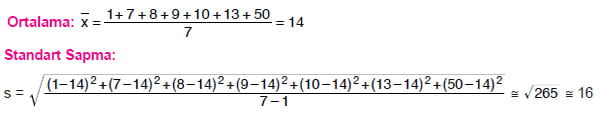
Ziyaretçi Sorusu: 3,4,4,4,5 dizisinin standart sapması nedir ?

Çözüm: Öncelikle elimizdeki 5 verinin aritmetik ortalaması (3+4+4+4+5)/5 = 4 çıkar.
S = karekök [(3-4)^2 + (4-4)^2 + (4-4)^2 + (4-4)^2 + (5-4)^2] / 4
S = (karekök2) / 4 = 0,35…

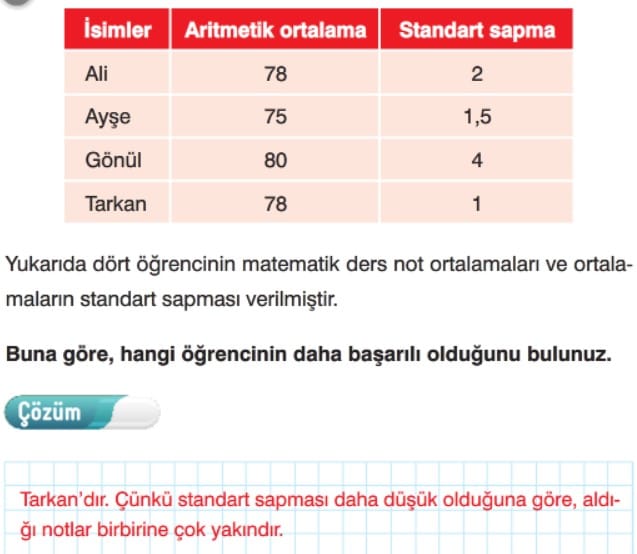
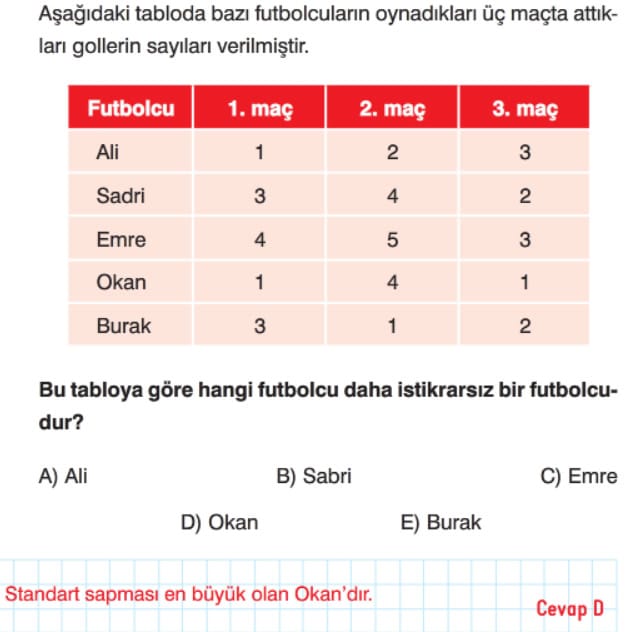
Standart Sapma Çözümlü Sorular

Çözümlü Test Soruları

1. Standart sapma ile ilgili aşağıdaki ifadelerden hangisi yanlıştır?
A) Verilerin dağılımının genişliğini ölçer
B) Aritmetik ortalamadan sapmaların karelerinin ortalamasının kareköküdür
C) Küçük değer alması verilerin homojen olduğunu gösterir
D) Veri grubundaki en büyük ve en küçük değerin farkıdır

Çözüm:
Standart sapma, verilerin ortalamadan ne kadar saptığını gösterir, en büyük-en küçük değer farkına “açıklık” denir. Doğru cevap D‘dir.

2. Bir sınıftaki 5 öğrencinin matematik notları: 70, 80, 85, 90, 95’tir. Bu veri grubunun standart sapması yaklaşık kaçtır?
A) 5,2
B) 8,4
C) 10,6
D) 12,8

Çözüm:

1. Ortalama = (70+80+85+90+95)/5 = 84

2. Sapmaların kareleri: (70-84)²=196, (80-84)²=16, (85-84)²=1, (90-84)²=36, (95-84)²=121

3. Varyans = (196+16+1+36+121)/5 = 370/5 = 74

4. Standart sapma = √74 ≈ 8,6 (En yakın seçenek B)

3. Aşağıdaki veri gruplarından hangisinin standart sapması en küçüktür?
A) 10, 20, 30, 40, 50
B) 15, 18, 20, 22, 25
C) 100, 100, 100, 100, 100
D) 5, 10, 15, 20, 25

Çözüm:
C seçeneğindeki tüm veriler aynı olduğu için standart sapma 0’dır (en küçük). Doğru cevap C‘dir.

4. Bir veri grubuna ait standart sapma hesaplandığında 0 çıkıyorsa bu ne anlama gelir?
A) Veriler çok heterojendir
B) Tüm veriler birbirine eşittir
C) Hesaplamada hata yapılmıştır
D) Veri sayısı yetersizdir

Çözüm:
Standart sapmanın 0 olması tüm veri değerlerinin eşit olduğunu gösterir. Doğru cevap B‘dir.

5. X = {2, 4, 6, 8, 10} veri grubunun standart sapması σ olduğuna göre, Y = {12, 14, 16, 18, 20} veri grubunun standart sapması nedir?
A) σ
B) σ+10
C) 2σ
D) σ²

Çözüm:
Y grubu X grubunun her elemanına +10 eklenerek oluşmuştur. Standart sapma verilere sabit eklenmesinden etkilenmez. Doğru cevap A‘dır.