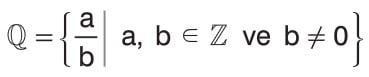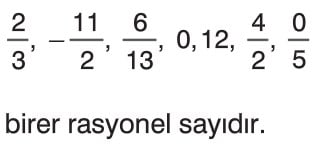Rasyonel sayılar Kümesi 9. Sınıf
Rasyonel Sayı: a ve b birer tam sayı ve b ≠ 0 olmak üzere, a/b şeklindeki ifadelere rasyonel sayılar denir. Rasyonel sayılar kümesi Q sembolü ile gösterilir.
Burada a ya pay, b ye de payda denir.
Örneğin;
- İki rasyonel sayı arasında sonsuz sayıda rasyonel sayı bulunabilir. Bu nedenle, rasyonel sayılar yoğundur denir.
- a sıfırdan farklı tam sayı olmak üzere, a / 0 ifadesi tanımsızdır.
- Her tam sayı bir rasyonel sayıdır. Diğer bir ifadeyle, tam sayılar kümesi rasyonel sayılar kümesinin bir alt
kümesidir. Yani, Z ⊂ Q olur.
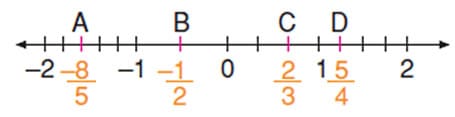
Rasyonel sayılar sayı doğrusu üzerinde gösterilebilir. Aşağıda sayı doğrusu üzerinde rasyonel sayılardan bir kaçı gösterilmiştir.
Rasyonel Sayılarda Dört İşlem

Devirli Ondalık Sayılar

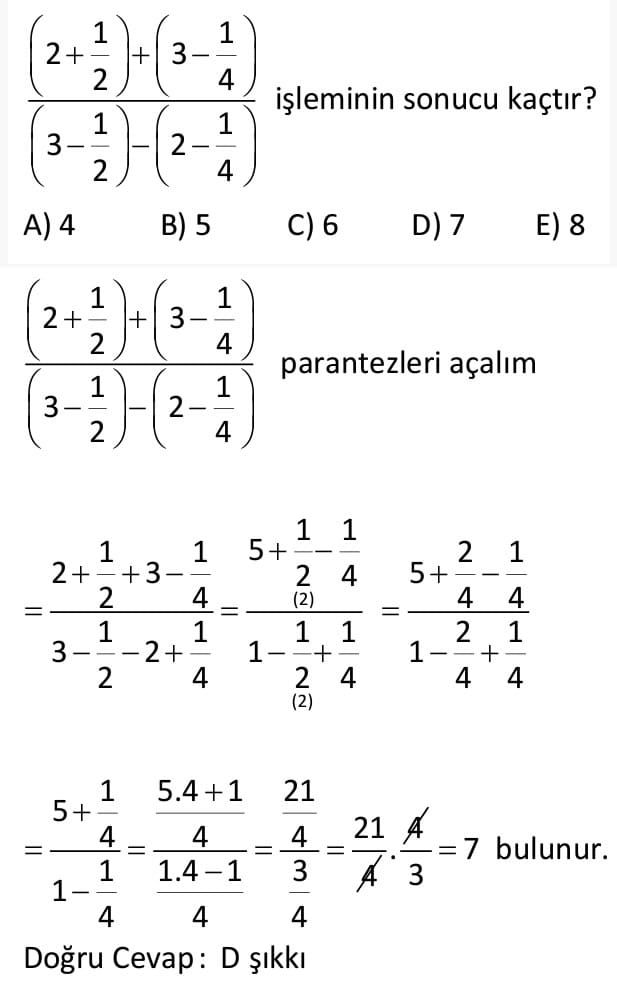
Rasyonel Sayılar Çözümlü Sorular
Rasyonel sayılar konu anlatımı 9. Sınıf çözümlü sorular Dört İşlem Devirli Ondalık Sayılar
Rasyonel Sayı: a ve b birer tam sayı ve b sıfırdan farklı olmak üzere a/b şeklinde ifade edilebilen sayılara rasyonel sayılar denir. a / b kesrinde a ya pay, b ye payda, a ile b arasındaki çizgiye de kesir çizgisi denir. Rasyonel sayılar kümesi Q ile gösterilir.
- Her tam sayı paydası 1 olan rasyonel sayıdır. Paydası sıfır olan rasyonel sayı tanımsızdır. Pay sıfır payda sıfırdan farklı ise o rasyonel sayı sıfıra eşittir.
- Tam sayılar kümesi rasyonel sayılar kümesinin alt kümesidir.
Kesirlerde Sadeleştirme ve Genişletme
a/b kesrinin pay ve paydasını sıfırdan farklı bir sayı ile çarpmaya genişletme, pay paydasını sıfırdan farklı bir sayıya bölmeye sadeleştirme denir.
Rasyonel sayılarda toplama ve çıkarma işlemi
- Rasyonel sayıların paydaları eşit ise paylar kendi arasında toplanır veya çıkarılır ve tek bir paydada yazılır.
- Paydalar eşit değil ise genişletme işlemi yapılarak paydalar eşitlenir ve sonra işlem yapılır.
Tam Sayılı Kesir

Tam Sayılı Kesre Çevirme

Rasyonel Sayılarda Toplama İşleminin Özellikleri
Rasyonel sayılarda toplama işleminin kapalılık, değişme, birleşme, etkisiz eleman ( sıfır ) ve ters eleman özellikleri vardır.
Rasyonel sayılarda çarpma işlemi
Pay ile pay, payda ile payda çarpılır. Payda eşitlemesi söz konusu değildir.
Rasyonel Sayılarda Çarpma İşleminin Özellikleri
Rasyonel sayılarda çarpma işleminin kapalılık, değişme, birleşme, etkisiz eleman ( bir), ters eleman ve yutan eleman özellikleri vardır.
Rasyonel sayılarda bölme işlemi
Rasyonel sayılarda bölme işlemi yapılırken ilk kesir aynen yazılır, ikinci kesir ters çevrilerek çarpma işlemi yapılır.
Ondalık Sayılar
Paydası 10'un kuvveti olarak yazılabilen rasyonel sayılara ondalık sayılar denir. Ondalık sayılarda toplama ve çıkarma işlemi yapılırken virgüller alt alta getirilerek işlem yapılır. Virgülün sağında eksik kalan basamaklar sıfır olarak alınır. Rasyonel sayılar çarpılırken virgül yokmuş gibi çarpma işlemi yapılır ve bulunan sayıda, çarpanların sağındaki toplam basamak kadar virgül sola kaydırılır. Rasyonel sayılarda bölme işlemi yapılırken virgülden kurtuluncaya kadar genişletme işlemi yapılır.
Devirli Ondalık Sayılar
Rasyonel sayı ondalık sayı olarak yazıldığında ondalık sayının virgülden sonraki rakamları belli bir kurala göre devam eden sayılara devirli ondalık sayılar denir.

Rasyonel Sayılarda Sıralama
- Paydalar eşit ise payı büyük olan daha büyüktür.
- Paylar eşit ise paydası küçük olan daha büyüktür.
- Pay ile payda arasındaki farklar eşit ise; bileşik kesirlerde paydası büyük olan küçüktür, basit kesirlerde paydası büyük olan büyüktür.
Yukarıdaki hiç bir kuralı kullanamıyorsak rasyonel sayı ondalık sayıya çevrilerek sıralama yapılır.
Ondalık Sayı, Devirli Ondalık Sayı: Paydası 10 un pozitif tam kuvveti olan kesirlere ondalıklı sayı denir. Bir rasyonel sayı, ondalıklı sayı biçiminde yazıldığında, sayının virgülden sonraki rakamları belli bir kurala göre tekrarlanıyorsa bu sayıya devirli (periyodik) ondalık sayı denir.
Her ondalık sayı bir rasyonel sayıdır. Bunun karşıtı da doğrudur. Her rasyonel sayı bir ondalık sayı biçiminde yazılabilir.
Rasyonel sayılar devirli ondalık sayı biçiminde yazılabilir.