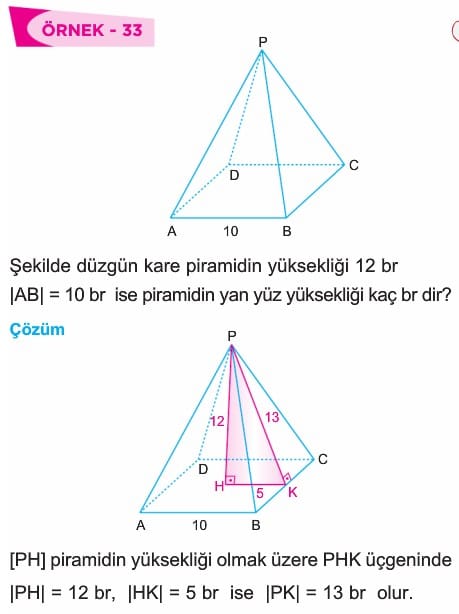
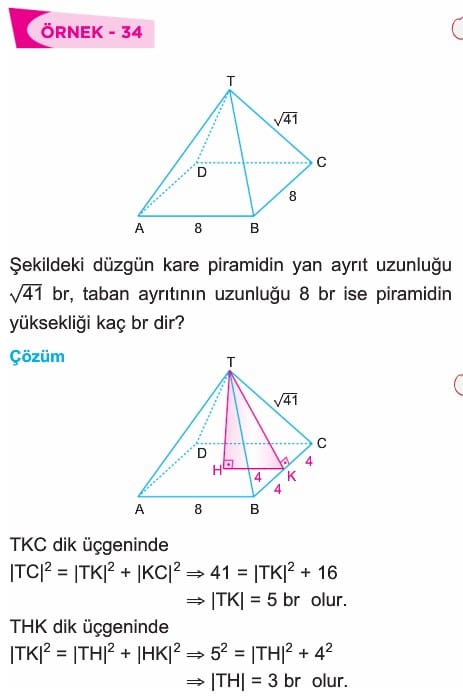
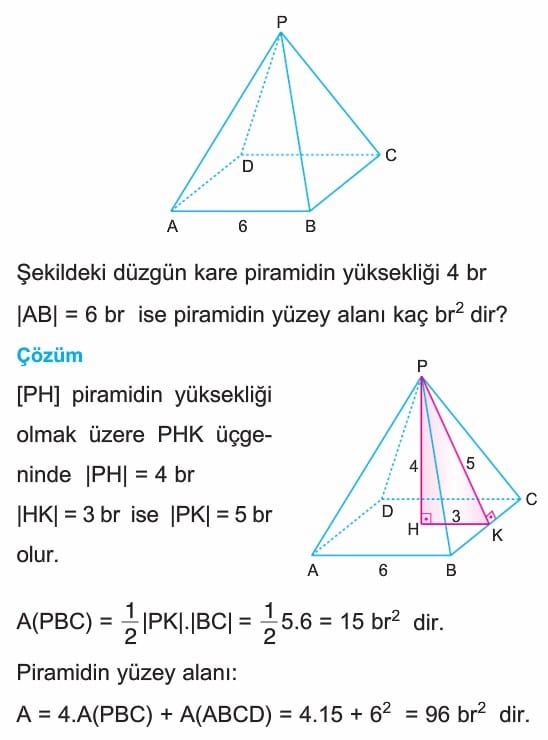
Piramitler Özellikleri, Alanı ve Hacmi 10. Sınıf Matematik
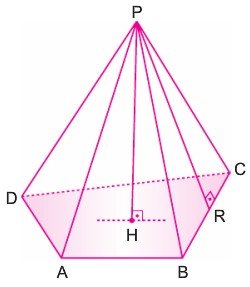
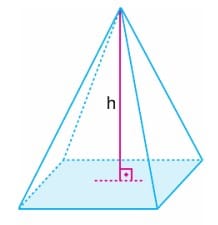
Piramit Bir çokgen ile bu çokgenin düzlemi dışında bir nokta verildiğinde, çokgenin bütün noktalarını dışındaki noktaya birleştirerek elde edilen cisme piramit denir. Piramitler tabanlarındaki çokgenin türüne göre adlandırılırlar. Aşağıdaki piramit, bir dörtgen piramittir.
- P, piramidin tepe noktasıdır.
- ABCD piramidin tabanıdır.
- [PA], [PB], [PC], [PD] doğru parçaları piramidin yan ayrıtlarıdır.
- PDA, PAB, PBC, PDC üçgensel bölgeleri piramidin yan yüzleridir.
- Tepe noktasının taban düzlemine olan uzaklığı piramidin yüksekliğidir. (|PH| = h)
- [PR] piramidin yan yüz yüksekliğidir.
Tepe noktası ile piramidin tabanı olan çokgenin ağırlık merkezini birleştiren doğru parçası çokgenin düzlemine dik ise bu piramitlere dik piramit ve bu doğru parçasının uzunluğuna ise dik piramidin yüksekliği denir.
Düzgün Piramit
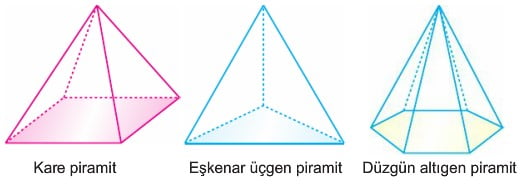
Tabanı düzgün çokgen olan ve yükseklik ayağı taban merkezinde bulunan piramide düzgün piramit denir. Aşağıdaki piramitler düzgün piramide birer örnektir. Düzgün piramitlerde:
- Yan ayrıt uzunlukları eşittir.
- Yan yüz yükseklikleri eşittir.
- Yan yüzler birbirine eş ikizkenar üçgenlerdir.
- Bir yan yüz yüksekliğine düzgün piramidin apotemi denir.
Kesik Piramit
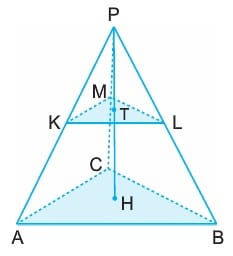
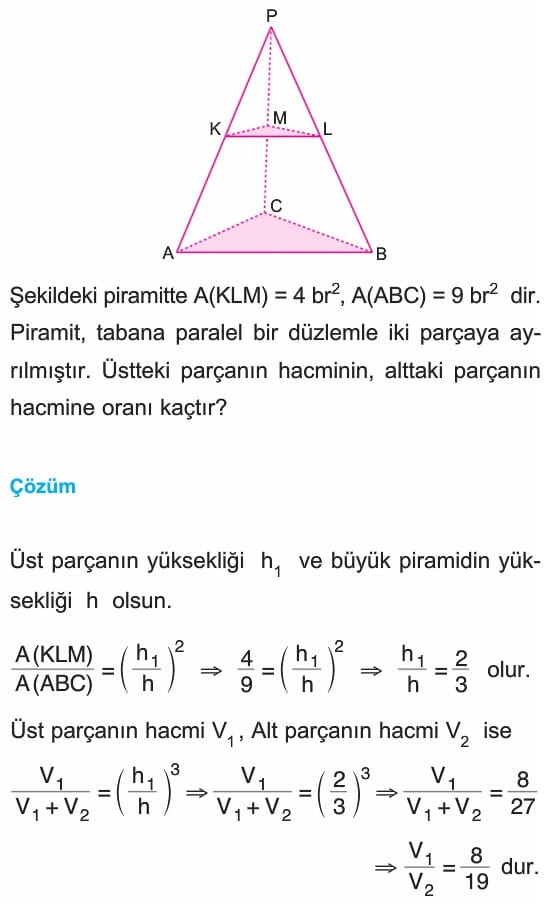
Bir piramit tabana paralel bir düzlemle kesildiğinde kesit düzlemi ile piramidin tabanı arasında kalan cisme kesik piramit denir.
Yukarıdaki şekilde ABC ile KLM arasındaki cisim bir kesik piramittir. [PH], ABC üçgensel bölgesine dik olmak üzere KLM kesit düzlemi ile ABC taban düzlemi benzerdir. ABC ~ KLM
Düzgün Kesik Piramit
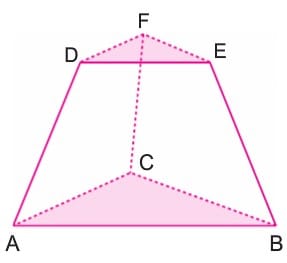
Şekilde düzgün bir piramidin tabana paralel bir düzlemle kesilmesi sonucu oluşan düzgün kesik piramit görülmektedir.
Düzgün kesik piramitte
- Tabanlar birbirlerine paralel birer düzgün çokgendir.
- Yan yüzler eş ikizkenar yamuklardır.
- Tabanların ağırlık merkezlerini birleştiren doğru, kesik piramidin yüksekliğidir.
DÜZGÜN PİRAMİDİN ALANI
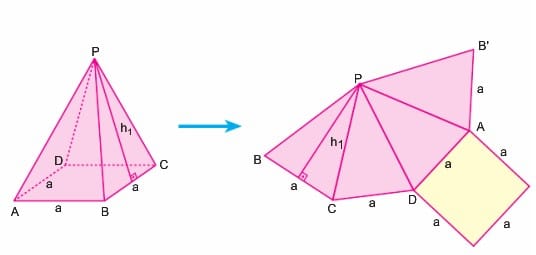
Yukarıdaki şekilde bir kare piramit ve açınımı verilmiştir. Bu düzgün piramidin yanal alanı, taban çevresi ile yan yüz yüksekliğinin çarpımına eşit olacağından
Bir düzgün piramidin alanı yanal alanı ile taban alanının toplamına eşittir.
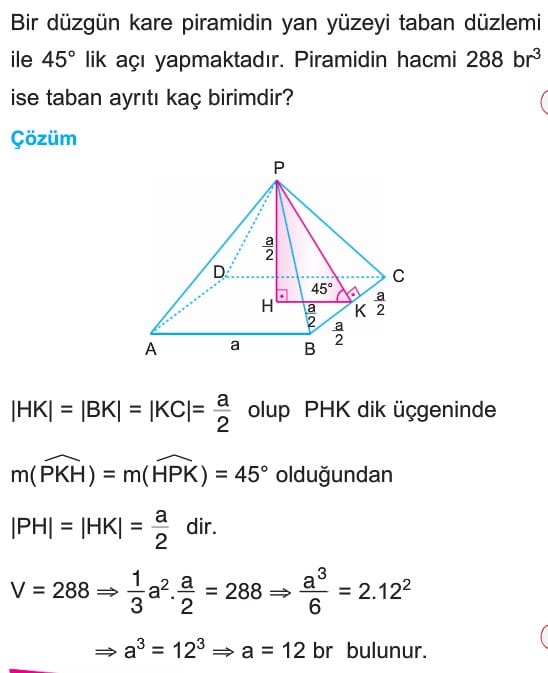
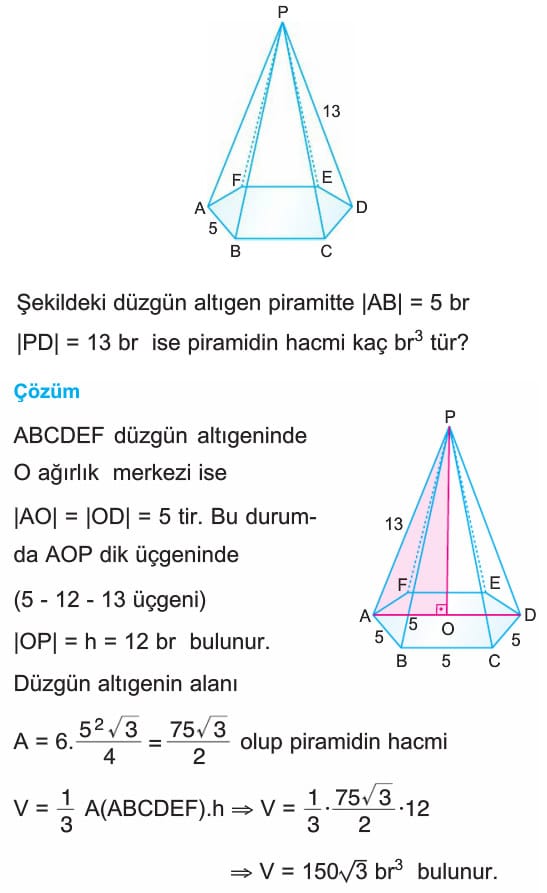
PİRAMİDİN HACMİ
Çözümlü Sorular
DÜZGÜN DÖRTYÜZLÜ
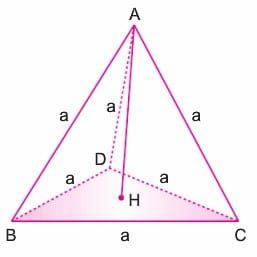
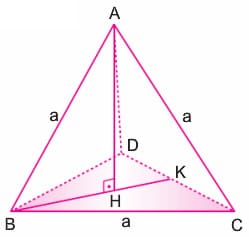
Dört yüzü de eşkenar üçgen olan piramide düzgün dörtyüzlü denir.
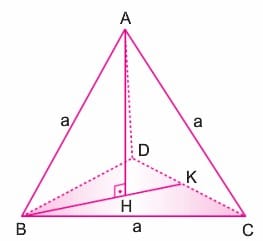
Piramidin yükseklik ayağı (H) tabandaki DBC üçgeninin ağırlık merkezidir.
Düzgün Dörtyüzlünün Yüksekliği
[BK], BCD eşkenar üçgeninin yüksekliği olduğundan
H noktası BCD üçgeninin ağırlık merkezi olduğundan
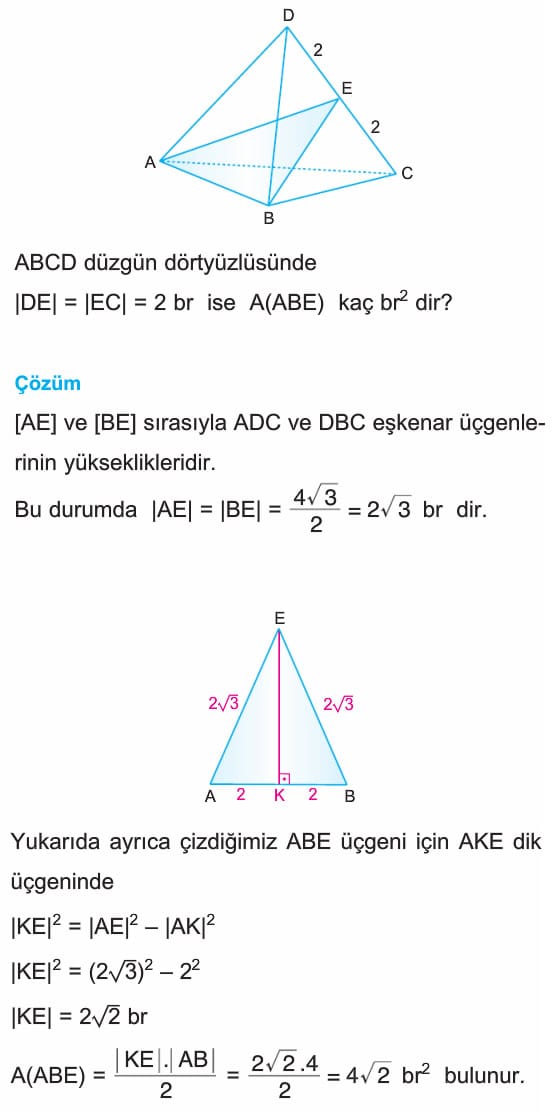
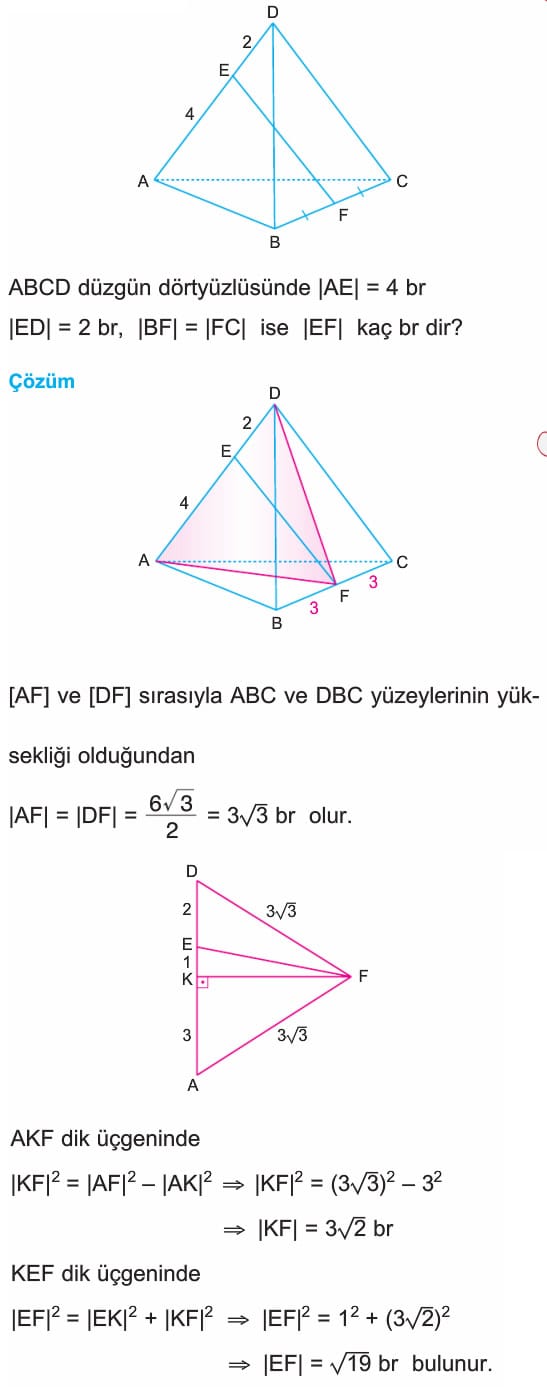
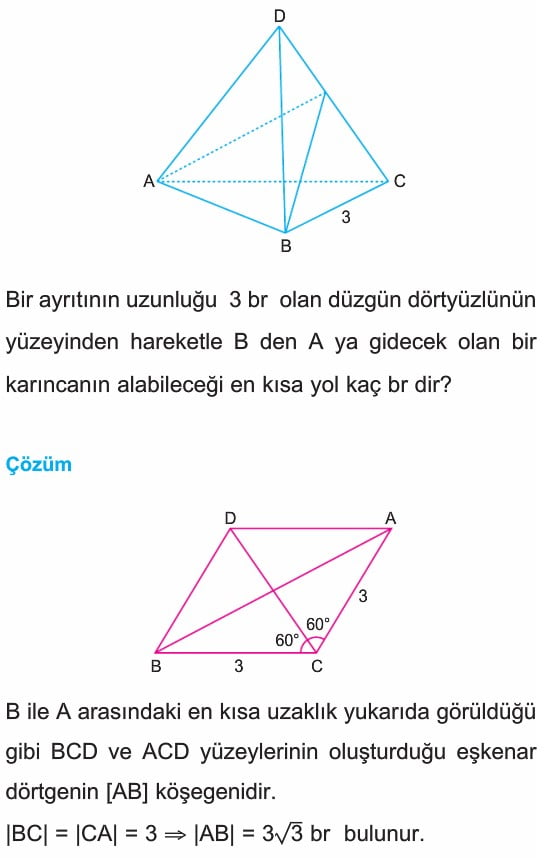
Çözümlü Sorular
Düzgün Dörtyüzlünün Alanı
Düzgün Dörtyüzlünün Hacmi
Bir ayrıtının uzunluğu a br olan düzgün dörtyüzlünün yüksekliğinin
birim olduğunu biliyoruz. Düzgün dörtyüzlü bir piramit olup hacmi
Dik Piramitler konu anlatımı Alanı Hacmi Düzgün Dörtyüzlü 10. Sınıf çözümlü sorular
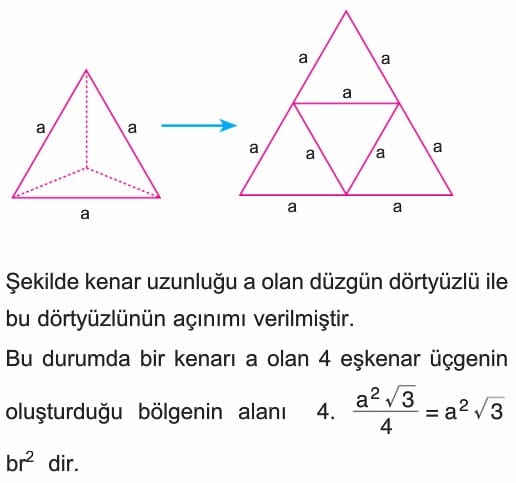
Şekilde kenar uzunluğu a olan düzgün dörtyüzlü ile bu dörtyüzlünün açınımı verilmiştir. Bu durumda bir kenarı a olan 4 eşkenar üçgenin oluşturduğu bölgenin alanı a2 kök 3 br2 dir.