5. Sınıf Gerçek Yaşam Problemleri, Doğal Sayı Problemleri Çözümleri, Çalışma Kağıdı

Gerçek yaşam problemleri, günlük hayatta karşılaştığımız olayları ve durumları çözmek için matematiksel işlemler kullanmayı ifade eder. Bu işlemler genellikle doğal sayılarla toplama, çıkarma, çarpma ve bölme gibi temel matematiksel becerilere dayanır. Bu problemleri çözerken öğrenciler, matematiksel düşünme yeteneklerini geliştirdikleri gibi, matematiğin hayatımızdaki yerini de kavrarlar.

5. Sınıf Matematik Doğal Sayılar ve İşlemler Konu Anlatımları
5. Sınıf Çok Basamaklı Sayıları Okuma ve Yazma
5. Sınıf Doğal Sayılarda Basamak Değeri
5. Sınıf Doğal Sayılarda Çözümleme
5. Sınıf Doğal Sayıları Karşılaştırma
5. Sınıf Dört İşlem Gerektiren Problemler (Gerçek Yaşam Problemleri)

5. Sınıf Gerçek Yaşam Problemleri (Dört İşlem Gerektiren Problemler) Ders Notu (Yeni Müfredat)

ZİHİNDEN TOPLAMA İŞLEMİ

Onluk ve Birliklerine Ayırma

Toplanacak doğal sayılar onluklarına ve birliklerine ayrılarak toplama işlemlerinin yapıldığı stratejidir. Onluklar toplanarak bulunan sonuç birliklerin toplamına eklenir.

Örnek: 85 + 38 işleminin sonucunu onluklarına ve birliklerine ayırarak zihinden toplama stratejisiyle bulalım.
85 → 80 + 5
38 → 30 + 8
80 + 30 = 110
8 + 5 = 13
110 + 13 = 123

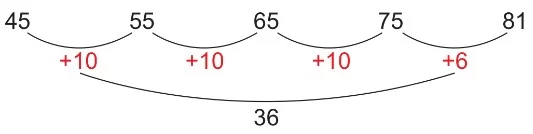
Onar – Onar Üzerine Sayma

Toplanacak sayılardan herhangi birinin üzerine diğer toplanan onar onar eklenir ve son olarak birlikler eklenerek toplam bulunur.

Örnek: 45 + 36 işleminin sonucunu onar onar üzerine sayma stratejisiyle bulalım.

10’u Referans Alarak Parçalama

Toplanacak doğal sayılardan bir tanesi en yakın onluğa tamamlanacak şekilde diğer sayı eksiltilir ve sayılar toplanır.

Örnek: 76 + 45 işleminin sonucunu 10’u referans alarak parçalama stratejisiyle bulalım.

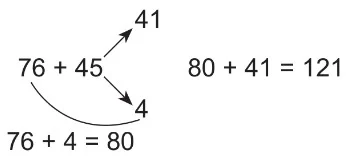
45 sayısını 76’yı en yakın onluğa tamamlayacak şekilde 41 + 4 olarak yazarız.

Kolay Toplanan Sayılardan Başlama

Toplanacak doğal sayılarda işleme birler basamağındaki rakamların toplamı 10 olan sayılardan başlanarak yapılan zihinden toplama stratejisidir.

Örnek: 27 + 18 + 13 işleminin sonucunu kolay toplanan sayılardan başlama stratejisiyle bulalım.
27 ve 13 doğal sayılarının birler basamakları toplamı 10 yaptığı için işleme bu sayılardan başlarız.
27 + 13 + 18 = 40 + 18 = 58

Örnek: Aşağıda verilen toplama işlemlerinin sonuçlarını belirtilen toplama stratejilerini kullanarak bulunuz.

a. Onluk ve Birliklerine Ayırma
a) 76 + 24 = 100
b) 48 + 25 = 73

b. Onar – Onar Üzerine Sayma
a) 65 + 22 =
b) 59 + 37 =

c. 10’u Referans Alarak Parçalama
a) 38 + 25 = 63
b) 46 + 38 = 84

d. Kolay Toplanan Sayılardan Başlama
a) 122 + 149 + 38 = 309
b) 78 + 55 + 25 = 158

ZİHİNDEN ÇIKARMA İŞLEMİ

Çıkan Sayıyı Onluk ve Birliklerine Ayırarak Eksiltme

Eksilen sayıdan ilk olarak çıkan sayının onlukları çıkarılır, ardından çıkan sayının birlikleri çıkarılarak işlemin sonucu bulunur.
Örnek: 78 – 43 işleminin sonucunu çıkan sayıyı onluk ve birliklerine ayırarak bulalım.
43 = 40 + 3
78 – 40 = 38
38 – 3 = 35

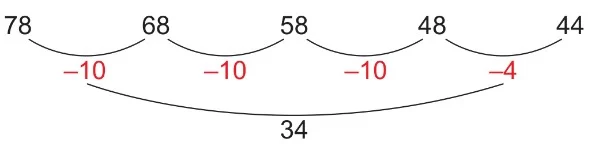
Eksilen Sayıyı Çıkan Sayı Kadar Onar Onar Eksiltme

Eksilen sayıdan çıkan sayı onar onar eksiltilir, ardından çıkan sayının birlikleri çıkarılarak işlemin sonucu bulunur.
Örnek: 78 – 34 işleminin sonucunu çıkan sayı kadar onar onar eksiltme stratejisiyle bulalım.

Sayıları Onluk ve Birliklerine Ayırarak Çıkarma

Eksilen ve çıkan sayılar onluk ve birliklerine ayrılarak ilk önce onlukların farkı bulunur ardından birliklerin farkı bulunarak sonuçlar toplanır.

Örnek: 67 – 34 işleminin sonucu sayıları onluk ve birliklerini ayırarak çıkarma stratejisinden yararlanarak bulalım.
67 = 60 + 7
34 = 30 + 4
60 – 30 = 30
7 – 4 = 3
30 + 3 = 33

Örnek: Aşağıdaki verilen çıkarma işlemlerinin sonuçlarını belirtilen çıkarma stratejilerini kullanarak bulunuz.

a. Çıkan Sayıyı Onluk ve Birliklerine Ayırarak Eksiltme
a) 127 – 83 = 44
b) 92 – 41 = 51

b. Eksilen Sayıyı Çıkan Sayı Kadar Onar Onar Eksiltme
a) 119 – 37 = 82
b) 245 – 74 = 171

c. Sayıları Onluk ve Birliklerine Ayırarak Çıkarma
a) 93 – 44 = 49
b) 127 – 65 = 62

Örnek: Aşağıdaki çıkarma işlemlerini zihinden yapınız. Hesap makinesi kullanarak sonucunuzu doğruluğunu kontrol ediniz.

a) 86 – 23 = 63
b) 94 – 29 = 65
c) 78 – 46 = 32
d) 79 – 15 = 64
e) 42 – 39 = 3
f) 51 – 23 = 28
g) 50 – 18 = 32
h) 49 – 25 = 24

ZİHİNDEN ÇARPMA İŞLEMİ

10, 100, 1000 ve Katlarıyla Zihinden Çarpma

Çarpma yaparken çarpanların sıfırları düşünülmeden işlem yapılır, çarpma işlemi sonrasında sıfırlar eklenir.

Örnek:

5 ile Zihinden Çarpma

Sayı, 10 ile çarpıldıktan sonra 2’ye bölünerek bulunabilir.

Örnek: 36 × 5 işlemini yapalım.

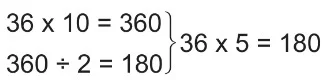
4 ve 8 ile Zihinden Çarpma

4 ile zihinden çarpma, sayının iki kez iki katı alınarak; 8 ile zihinden çarpma ise sayının üç kez iki katı alınarak yapılabilir.

Örnek: 24 × 4 işlemini yapalım.
24 × 2 = 48
48 × 2 = 96

Örnek: 15 × 8 işlemini yapalım.
15 × 2 = 30

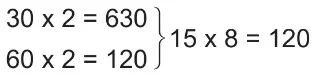
9 ve 11 ile Zihinden Çarpma

9 ile zihinden çarpma, sayı 10 ile çarpıldıktan sonra sonuçtan kendisi çıkarılarak yapılır. 11 ile zihinden çarpma ise sayı 10 ile çarpıldıktan sonra sonuç üzerine kendisi eklenerek yapılır.

Örnek: 12 × 9 işlemini yapalım.
12 × 10 = 120
120 – 12 = 108

Örnek: 12 × 11 işlemini yapalım.
12 × 10 = 120
120 + 12 = 132

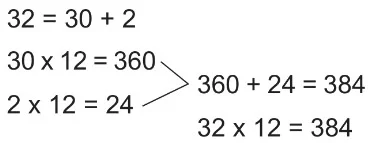
Onluk ve Birliklere Ayırarak Çarpma

Çarpanlardan birinin onluk ve birliklerine ayırılarak sırasıyla diğer sayı ile çarpılıp bulunan sonuçların toplanmasıyla yapılabilir.

Örnek: 32 × 12 işlemini yapalım.

Örnekler

Aşağıdaki 10, 100, 1000 ve Katlarıyla Çarpma İşlemlerini Zihinden Yapınız.
a) 130 × 100 = 13 000
b) 70 × 3000 = 210 000
Aşağıdaki 5 ile Çarpma İşlemlerini Zihinden Yapınız.
a) 46 × 5 = 230
b) 39 × 5 = 195
Aşağıdaki 4 ve 8 ile Çarpma İşlemlerini Zihinden Yapınız.
a) 180 × 4 = 720
b) 22 × 8 = 176
Aşağıdaki 9 ve 11 ile Çarpma İşlemlerini Zihinden Yapınız.
a) 13 × 9 = 117
b) 43 × 11 = 473
Aşağıdaki Çarpma İşlemlerini Çarpanlardan Birini Onluk ve Birliklerine Ayırarak Zihinden Yapınız.
a) 23 × 6 = 138
b) 18 × 15 = 270

ZİHİNDEN BÖLME İŞLEMİ

Son Basamaklarında Sıfır Bulunan Sayılarla Bölme İşlemi

Son basamaklarında sıfır bulunan sayılarla bölme işlemi yaparken bölen ve bölünen sayılardan eşit sayıda sıfır silinir. Sonra kalan sayılarla bölme işlemi yapılır.

Örnek:

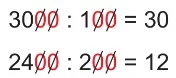
5 ile Zihinden Bölme İşlemi

Bir sayı 5 ile zihinden bölünürken sayı önce 2 ile çarpılıp daha sonra 10’a bölünerek sonuç bulunabilir.

Örnek: 75 ÷ 5 işlemini yapalım.

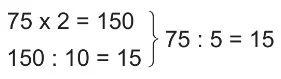
4 ve 8 ile Zihinden Bölme İşlemi

Bir sayı 4 ile zihinden bölünürken sayı iki defa 2 ile bölünerek, 8 ile zihinden bölünürken sayı üç defa 2 ile bölünerek sonuç bulunabilir.

Örnek: 84 ÷ 4 işlemini yapalım.

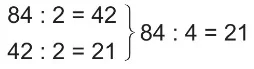
Örnek: 120 ÷ 8 işlemini yapalım.

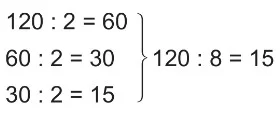
Örnek: Aşağıdaki 10, 100, 1000 ve Katlarıyla Bölme İşlemlerini Zihinden Bölme Stratejilerini Kullanarak Yapınız.
a) 5600 ÷ 100 = 56
b) 3200 ÷ 20 = 160

Örnek: Aşağıdaki 5 ile Bölme İşlemlerini Zihinden Bölme Stratejilerini Kullanarak Yapınız.
a) 65 ÷ 5 = 13
b) 110 ÷ 5 = 22

Örnek: Aşağıdaki 4 ve 8 ile Bölme İşlemlerini Zihinden Bölme Stratejilerini Kullanarak Yapınız.
a) 100 ÷ 4 = 25
b) 240 ÷ 8 = 30

Örnek: Aşağıdaki İşlemlerin Sonucunu Önce Tahmin Ediniz, Sonra İşlem Yaparak Bulunuz.
a) 482 + 366 = 848
b) 775 – 342 = 433
c) 43 × 32 = 1376
d) 288 ÷ 12 = 24

Örnek: Handan parasıyla tanesi 40 TL olan kalemlerden 12 tane, tanesi 30 TL olan silgilerden 5 tane almıştır. Handan’ın bu alışverişten sonra 90 TL’si kalmıştır.
Buna göre, Handan başlangıçtaki parası ile kaç tane kalem alabilirdi?

Çözüm:

Kalemlerin maliyeti:
12 tane kalem × 40 TL = 480 TL
Silgilerin maliyeti:
5 tane silgi × 30 TL = 150 TL
Toplam harcama:
480 TL (kalemler) + 150 TL (silgiler) = 630 TL
Handan’ın başlangıçtaki parası:
Handan’ın 90 TL’si kalmıştı, bu nedenle başlangıçtaki parası 630 TL (harcama) + 90 TL (kalan) = 720 TL
Handan’ın başlangıçtaki parası ile alabileceği kalem sayısı:
720 TL ÷ 40 TL = 18 tane kalem

DOĞAL SAYILARDA TOPLAMA İŞLEMİ

Doğal sayılarla toplama işlemi yapılırken sayılar aynı basamaklar alt alta gelecek şekilde yazılarak işlem yapılır. Eğer basamaklardaki sayıların toplamında 10’dan büyük bir sayı varsa elde bir sonraki basamağa eklenir.

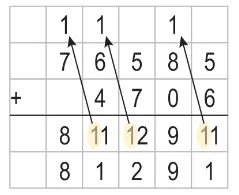
Yukarıda verilen işlemin sonucu 81 291’dir.

Toplama işleminde terimler aşağıda gösterildiği gibi isimlendirilir.

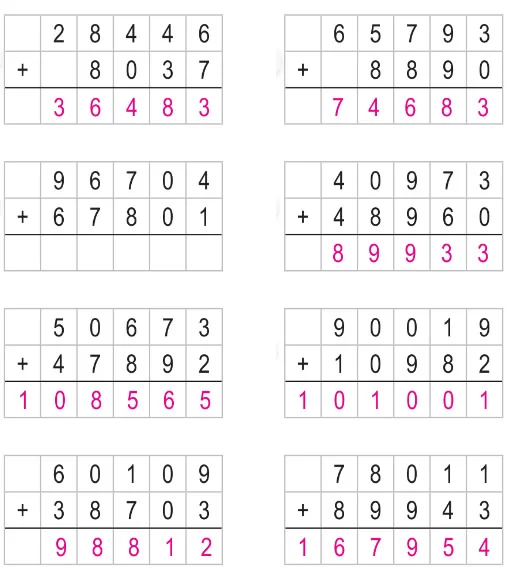
Örnek: Aşağıda verilen toplama işlemlerinin sonuçlarını bulunuz.

Soru: Bir depoya gelen iki araçtan birincisi 13 438 kg buğday, diğeri ise 17 427 kg buğday getirmiştir.
Buna göre depoya gelen toplam buğday miktarı kaç kilogramdır?

Çözüm:
13 438 kg + 17 427 kg = 30 865 kg

Soru: Esma’nın bilgisayarına indirdiği 3 dosyanın boyutları aşağıda verilmiştir:

Film Arşivi = 72 928 megabayt
Müzik Arşivi = 19 209 megabayt
Fotoğraf Arşivi = 28 789 megabayt
Buna göre Esma’nın indirdiği dosyaların toplam boyutu kaç megabayttır?

Çözüm:
72 928 MB + 19 209 MB + 28 789 MB = 120 926 megabayt

Soru: Bir motosiklet satıcısında bulunan motorlardan bir tanesi 78 457 TL, diğeri ise bu motordan 13 411 TL pahalı olarak satılmaktadır.
Buna göre satıcıda bulunan motorların birer tanesinin fiyatları toplamı kaç Türk Lirasıdır?

Çözüm:
78 457 TL + (78 457 TL + 13 411 TL) = 78 457 TL + 91 868 TL = 170 325 TL

Soru: Yerden 18 476 birim yükseklikte uçan uçurtma 12 745 birim daha yükseldikten sonra ipi koparak aşağıya düşmüştür.
Uçurtmanın düştüğü yükseklik kaç birimdir?

Çözüm:
18 476 birim + 12 745 birim = 31 221 birim

DOĞAL SAYILARDA TOPLAMA İŞLEMİNİN SONUCUNU TAHMİN ETME

Doğal sayılarda toplama işlemlerinin sonucunu tahmin etmek için, toplanan sayılar istenilen basamağa yuvarlanarak toplama işlemi kolay şekilde yapılır. Bulunan sonuç tahmini sonuçtur.
Sayılar yuvarlanırken yuvarlanması istenilen basamağın sağında bulunan rakam;
5 veya 5’ten büyük (5, 6, 7, 8, 9) ise yuvarlanacak basamak bir arttırılır ve sağındaki basamaklara sıfır (0) yazılır.
5’ten küçük (0, 1, 2, 3, 4) ise yuvarlanacak basamak aynı şekilde bırakılarak sağındaki basamaklara sıfır (0) yazılır.

Örnek: 127 sayısını onlar basamağına yuvarlayalım.
Onlar basamağının sağındaki rakam 7, 5’ten büyük olduğu için onlar basamağındaki rakam bir arttırılır ve sağdaki rakamlar yerine sıfır yazılır.
Yani 127’nin onlar basamağına yuvarlanmış hâli 130 olur.

Örnek: 232 sayısını yüzler basamağına yuvarlayalım.
Yüzler basamağının sağındaki rakam 2, 5’ten küçük olduğu için yüzler basamağındaki rakam aynen yazılır ve sağındaki rakamlar yerine sıfır yazılır.
Yani 232’nin yüzler basamağına yuvarlanmış hâli 200 olur.

Soru: Aşağıda verilen tabloda beş gün boyunca havalimanından seyahat eden yolcu sayıları hakkında bilgiler verilmiştir.

Günler	Pazartesi	Salı	Çarşamba	Perşembe	Cuma
Yolcu Sayısı	18 403	21 279	19 419	30 987	38 809

Verilen tabloya göre aşağıdaki soruları cevaplayınız.

a. Perşembe ve Cuma günleri seyahat eden toplam yolcu sayısını toplanan sayıları en yakın onluğa yuvarlayarak tahmin ediniz.

Çözüm:

Perşembe günü yolcu sayısı: 30 987 → 30 990 (en yakın onluğa yuvarlama)
Cuma günü yolcu sayısı: 38 809 → 38 810 (en yakın onluğa yuvarlama)

Toplam yolcu sayısı:
30 990 + 38 810 = 69 800

b. Pazartesi ve Salı günleri seyahat eden toplam yolcu sayısını toplanan sayıları en yakın yüzlüğe yuvarlayarak tahmin ediniz.

Çözüm:

Pazartesi günü yolcu sayısı: 18 403 → 18 400 (en yakın yüzlüğe yuvarlama)
Salı günü yolcu sayısı: 21 279 → 21 300 (en yakın yüzlüğe yuvarlama)

Toplam yolcu sayısı:
18 400 + 21 300 = 39 700

DOĞAL SAYILARDA ÇIKARMA İŞLEMİ

Doğal sayılarla çıkarma işlemi yapılırken sayılar aynı basamaklar alt alta gelecek şekilde yazılarak işlem yapılır.

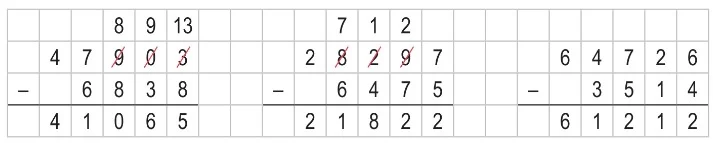
Çıkarma işleminde terimler aşağıda gösterildiği gibi isimlendirilir.
Eksilen – Çıkan = Fark
Çıkarma işleminde verilmeyen terimleri bulmak için: ➡ Çıkan terimi bulmak için eksilen sayıdan fark çıkarılır.
Eksilen – Fark = Çıkan

Örnekler:

a. Eksilen sayının 2715, farkın 418 olduğu bir çıkarma işleminde çıkan sayı kaçtır?
Çıkan sayıyı bulmak için eksilen sayıdan farkı çıkarırız.
2715 – 418 = 2297

b. Eksilen sayının 24 817, farkın 13 413 olduğu bir çıkarma işleminde çıkan sayı kaçtır?
24 817 – 13 413 = 11 404
➡ Eksilen sayıyı bulmak için fark ile çıkan sayı toplanır.

Çıkan + Fark = Eksilen

Örnekler:

a. Çıkan sayının 278, farkın 479 olduğu bir çıkarma işleminde eksilen kaçtır?
Eksilen sayıyı bulmak için çıkan sayı ile fark toplanır.
278 + 479 = 757

b. Çıkan sayının 41 714, farkın 26 819 olduğu bir çıkarma işleminde eksilen sayı kaçtır?
41 714 + 26 819 = 68 533

Toplama işleminde toplananlardan herhangi biri verilmediği zaman, toplandan verilen toplanan çıkarılarak verilmeyen toplanan bulunur.
1. Toplanan = Toplam – 2. Toplanan
2. Toplanan = Toplam – 1. Toplanan

Örnek: Boş ağırlığı 48 500 gram olan bir kap tamamı su ile doldurularak tartıldığında 92 378 gram gelmektedir. Buna göre kap içindeki suyun ağırlığı kaç gramdır?
Kap ile içerisindeki suyun ağırlığının toplamı 92 378 gram gelmektedir.
Yani;
Su + 48 500 = 92 378
Su = 92 378 – 48 500
Su = 43 878 gramdır.

DOĞAL SAYILARDA ÇIKARMA İŞLEMİNİN SONUCUNU TAHMİN ETME

Doğal sayılarda çıkarma işlemlerinin sonucunu tahmin etmek için sayılar istenilen basamağa yuvarlanır.
İstenilen basamağa yuvarlama yapıldıktan sonra çıkarma işlemi yapılarak tahmini sonuç hesaplanır.

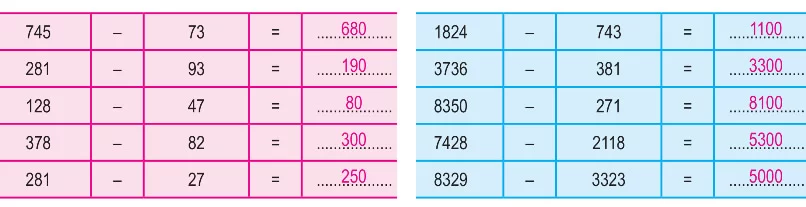
Soru: Aşağıda verilen çıkarma işlemlerinden pembe tablo içindeki işlemleri sayıları onlar basamağına yuvarlayarak, mavi tablo içindeki işlemleri ise sayıları yüzler basamağına yuvarlayarak tahmin ediniz.

Soru: Aşağıda verilen problemlerin sonuçlarını bulunuz.

a. Türkiye’nin deniz kıyıları toplam uzunluğu 8333 km’dir. Bu uzunluğun 1700 km’si Karadeniz kıyısı olduğuna göre diğer kıyı uzunluklarının uzunluğu kaç kilometredir?
Çözüm: Toplam kıyı uzunluğundan Karadeniz kıyısının uzunluğu çıkarılır.
Diğer kıyı uzunluklarının toplamı: 6633 km

b. Bir atölyede ocak ayındaki üretim sayısı 78 313’tür. Şubat ayındaki üretim sayısı ocak ayındaki üretim sayısından 21 934 daha az olduğuna göre şubat ayındaki üretim sayısı kaçtır?
Çözüm: Ocak ayındaki üretimden şubat ayındaki fark çıkarılır.
Şubat ayındaki üretim sayısı: 56 379

c. Eksilen sayının 92 109, farkın 27 231 olduğu bir çıkarma işleminde çıkan sayı kaçtır?
Çözüm: Eksilen sayıdan fark çıkarılarak çıkan sayı bulunur. Çıkan sayı: 64 878

d. Yerden 32 015 metre yükseklikte uçan bir uçak olumsuz hava koşulları nedeniyle 13 732 metre alçalmıştır. Buna göre uçağın yeni yüksekliğini sayıları binler basamağına yuvarlayarak tahmin ediniz.
Çözüm: Öncelikle uçak ne kadar alçaldıysa yeni yüksekliğini buluruz.
18 283 sayısını binler basamağına yuvarlayalım:
18 283, binler basamağına yuvarlandığında 18 000 olur.

DOĞAL SAYILARDA ÇARPMA İŞLEMİ

Doğal sayılarda çarpma işlemi yapılırken 2. çarpandaki sayının basamaklarındaki rakamlar birler basamağından başlanarak sırasıyla 1. çarpan ile çarpılır. Elde edilen sonuçlar ikinci sıfırdan itibaren birer basamak sola kaydırılarak alt alta yazılıp toplanır. Basamakların sola kaydırılma nedeni o basamakların sıfır (0) olmasıdır.

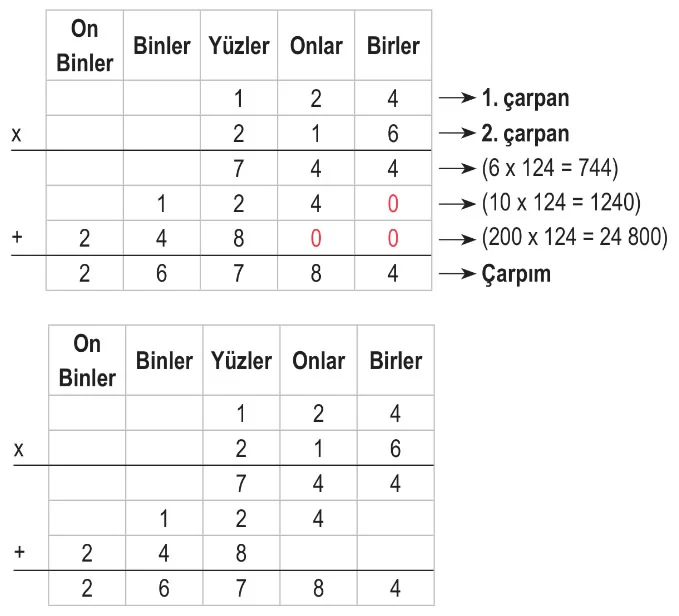
Örnek:

Örnek: Bir çiftlikteki ineklerden her gün 158 litre süt alınmaktadır. Bu çiftlikte 2 haftada ineklerden alınan toplam süt miktarı kaç litredir?
Çözüm: Bir haftada 7 gün vardır, 2 haftada ise 14 gün.
Her gün 158 litre süt alındığına göre,
2 haftada alınan toplam süt:
158 litre × 14 = 2212 litredir.

Örnek: Her gün 12 buzdolabı üreten bir fabrika bir yıl boyunca kaç tane buzdolabı üretir? (1 yıl = 365 gün)
Çözüm: Bir yılda 365 gün olduğuna göre:
12 buzdolabı × 365 gün = 4380 buzdolabı üretir.

Örnek: Hesap makinesinde 156 × 18 işlemini yapan Ceyhun 1. çarpanın onlar basamağını tuşlarken yanlışlıkla 4’e basmıştır. Buna göre bulduğu sonuç gerçek sonuçtan kaç fazladır?
Çözüm: Gerçek işlem: 156 × 18 = 2808
Yanlış hesaplanan işlem: 456 × 18 = 8208
Fark: 8208 – 2808 = 5400 fazla

Örnek: Üç basamaklı en küçük tek sayı ile iki basamaklı en büyük çift doğal sayının çarpımı kaçtır?
Çözüm: Üç basamaklı en küçük tek sayı 101’dir.
İki basamaklı en büyük çift sayı 98’dir.
101 × 98 = 9898.

Örnek: Saatte 45 dondurma üreten bir makine bir günde 16 saat çalışmaktadır. Buna göre bu makinenin bir ayda ürettiği dondurma sayısını zihinden hesaplayınız. (1 ay = 30 gün)
Çözüm: Bir günde üretilen dondurma sayısı: 45 × 16 = 720 dondurma.
Bir ayda üretilen dondurma sayısı: 720 × 30 = 21.600 dondurma

Örnek: Nejla Hanım evinin camları için metresi 27 TL olan kalın perdelik kumaştan 46 metre ve metresi 15 TL olan tül perde kumaştan 32 m almıştır. Nejla Hanım bu alışverişe toplam kaç TL ödemiştir?
Çözüm: Kalın perdelik kumaşın maliyeti: 46 metre × 27 TL = 1242 TL
Tül perdenin maliyeti: 32 metre × 15 TL = 480 TL
Toplam ödeme: 1242 TL + 480 TL = 1722 TL

DOĞAL SAYILARDA ÇARPMA İŞLEMİNİN SONUCUNU TAHMİN ETME

Çarpma işleminde aynı toplama ve çıkarma işleminde olduğu gibi sayıları en yakın onluğa veya en yakın yüzlüğe yuvarlayarak sonucu tahmin edebiliriz.

Örnek: 28 × 152 işlemini çarpanları en yakın onluğa yuvarlayarak tahmin edip gerçek sonuç ile tahmini sonuç arasındaki farkı bulalım.
Gerçek Sonuç: 28 × 152 = 4256
Tahmini Sonuç: 28 → 30, 152 → 150
30 × 150 = 4500
Tahmini sonuç – Gerçek sonuç = 4500 – 4256 = 244

Örnek: 482 × 269 işlemini çarpanları en yakın yüzlüğe yuvarlayarak tahmin edip gerçek sonuç ile tahmini sonuç arasındaki farkı bulalım.
Gerçek Sonuç: 482 × 269 = 83658
Tahmini Sonuç: 482 → 400, 269 → 200
400 × 200 = 80000
Gerçek sonuç – Tahmini sonuç = 83658 – 80000 = 3658

Örnek: Elif’in her biri 38 sayfalık 42 hikâye kitabı vardır. Elif’in hikâye kitaplarının toplam sayfa sayısını sayıları en yakın onluğa yuvarlayarak tahmin etmek istiyor.
Buna göre Elif’in bulduğu sonuç gerçek sonuçtan kaç fazladır?
Gerçek hesaplama:
38 × 42 = 1596 sayfa
Tahmini hesaplama (sayıları en yakın onluğa yuvarlayarak):
38 → 40
42 → 40
40 × 40 = 1600
Tahmini sonuç – Gerçek sonuç = 1600 – 1596 = 4 sayfa fazladır.

Örnek: Bir market içerisinde 72 şeker bulunan paketlerden 128 tane satmıştır. Marketin bir günde sattığı şeker sayısını, verilen sayıları en yakın onluğa yuvarlayarak tahmin ediniz.
Gerçek hesaplama:
72 × 128 = 9216 şeker
Tahmini hesaplama (sayıları en yakın onluğa yuvarlayarak):
72 → 70
128 → 130
70 × 130 = 9100
Tahmini sonuç – Gerçek sonuç = 9100 – 9216 = 116 şeker daha azdır.

DOĞAL SAYILARDA BÖLME İŞLEMİ

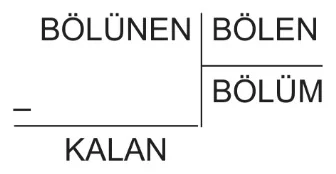
Bir bölme işleminde bölünen sayı, bölen ile bölümün çarpımı ile kalanın toplamına eşittir.
BÖLÜNEN = (BÖLEN x BÖLÜM) + KALAN

Örnek:

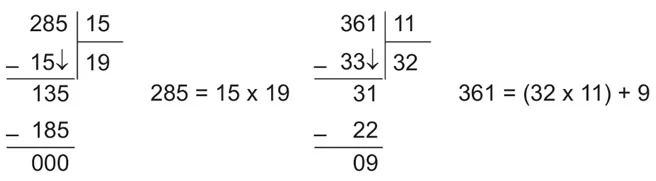
Bir bölme işleminde bölünen sayıdan rakam indirildiğinde oluşan sayıda bölen yoksa, tekrar rakam indirmek için bölüme sıfır (0) eklenir.

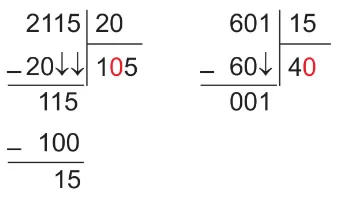
Örnek: Bir depodaki özdeş 2875 kutu, her biri en fazla 125 kutu alabilen eşit ölçüdeki raflara yerleştirilecektir.

a. Buna göre tüm kutuları yerleştirebilmek için en az kaç rafa ihtiyaç vardır?

Çözüm:

Toplam kutu sayısı: 2875
Her rafa yerleştirilebilecek kutu sayısı: 125
İhtiyaç duyulan raf sayısını bulmak için, toplam kutu sayısını raf kapasitesine böleriz: 2875 ÷ 125 = 23 raf
En az 23 raf gereklidir.

b. Kutuların her birinin ağırlığı 12 kilogram olduğuna göre bir rafa dizilen kutuların toplam ağırlığı en fazla kaç kilogramdır?

Çözüm:

Her kutu 12 kilogram ve bir rafa 125 kutu yerleştirilebiliyor.
Bir rafın maksimum ağırlığı: 125 x 12 = 1500 kilogramdır.

Örnek: Bir fabrikada bir günde üretilen 2830 kilogram unun tamamı, 12 veya 25 kilogramlık paketlere konulmaktadır. 12 kilogramlık paket 120 TL’ye, 25 kilogramlık paket ise 200 TL’ye satılmaktadır.

a. Bu fabrikada 115 tane 12 kilogramlık paket oluşturulduğunda bir gün kaç tane 25 kilogramlık paket oluşturulmuştur?

Çözüm:

115 tane 12 kilogramlık paket oluşturulmuş: 115 x 12 = 1380 kilogram un kullanılmıştır.
Geriye kalan un miktarı: 2830 – 1380 = 1450 kilogramdır.
Kalan un ile 25 kilogramlık paketler yapılacaktır: 1450 ÷ 25 = 58 paket oluşturulabilir.

b. Aynı gün 12 ve 25 kilogramlık paketlerin satışından elde edilecek toplam gelir kaç TL’dir?

Çözüm:

12 kilogramlık paketlerden 115 adet satılmış: 115 x 120 = 13.800 TL gelir elde edilmiştir.
25 kilogramlık paketlerden 58 adet satılmış: 58 x 200 = 11.600 TL gelir elde edilmiştir.
Toplam gelir: 13.800 + 11.600 = 25.400 TL olacaktır.

DOĞAL SAYILARDA BÖLME İŞLEMİNİN SONUCUNU TAHMİN ETME

Bölme işleminde aynı çarpma işleminde olduğu gibi sayıları en yakın onluğa veya en yakın yüzlüğe yuvarlayarak sonucu tahmin edebiliriz.

Örnek: 263 : 18 işlemini böleni ve bölüneni en yakın onluğa yuvarlayarak tahmin edelim.
263 → 260
18 → 20
Tahmini sonuç: 260 : 20 = 13

Örnek: 396 : 46 işlemini böleni en yakın yüzlüğe, bölüneni en yakın onluğa yuvarlayarak tahmin edelim.
396 → 400
46 → 50
Tahmini sonuç: 400 : 50 = 8

Üç veya dört basamaklı sayıları bir veya iki basamaklı sayılarla bölerken, sayının ilk iki basamağını bölünen en yakın katına yuvarlayıp diğer basamakları sıfırlayarak tahmini sonuç bulabiliriz.

Örnek: 334 : 8 işlemini, 334 sayısını ilk iki basamağını 8’in katı olacak şekilde yuvarlayarak tahmin edelim.
334 → 8’in 33’e en yakın katı 32 olduğundan, 334 sayısı 320’ye yuvarlanır.
Tahmini sonuç: 320 : 8 = 40

Örnek: Belma sınıftaki arkadaşlarına dağıtmak için 22 tane dondurma almış ve toplamda 616 TL ödemiştir. Bir dondurmanın fiyatını hesaplarken sayıları en yakın onluğa yuvarlayarak tahmin edecek olan Belma’nın bulduğu tahmini sonuç kaçtır?
Çözüm:
616 TL’yi ve 22 dondurmayı en yakın onluğa yuvarlayalım:
22 → 20 Dondurma
616 → 620 TL
20 dondurma için fiyat:
620 ÷ 20 = 31 TL
Tahmini sonuç: Bir dondurmanın tahmini fiyatı 31TL.

Örnek: Bir okul 312 öğrencisini 48 kişi kapasiteli otobüslerle geziye götürecektir. Bu iş için gerekli olan otobüs sayısını tahmini olarak hesaplayınız.
Çözüm:
312 öğrenci sayısını en yakın yüzlüğe ve 48 kişilik otobüs kapasitesini en yakın onluğa yuvarlayalım:
312 → 300
48 → 50
300 ÷ 50 = 6 otobüs
Tahmini sonuç: 6 otobüs

Örnek: Tolga 864 soruluk soru bankasını her gün 32 sorusunu çözerek bitirmek istemektedir. Tolga, soru bankasını kaç günde bitirebileceğini soru bankasındaki soru sayısını en yakın yüzlüğe, bir günde çözdüğü soru sayısını en yakın onluğa yuvarlayarak tahmin etmiştir. Buna göre Tolga kitabı kaç günde bitireceğini tahmin etmiştir?
Çözüm:
864 soruyu ve 32 soruyu en yakın yüzlük ve onluğa yuvarlayalım:
864 → 900
32 → 30
900 ÷ 30 = 30 gün
Tahmini sonuç: 30 gün.

Örnek: Bir boyacı aldığı bir işte 32 günde 2432 m²lik duvarı boyayacaktır. Boyacı bu işi tahminen kaç günde bitireceğini büyük sayıyı en yakın yüzlüğe, küçük sayıyı en yakın onluğa yuvarlayarak hesaplamıştır. Buna göre boyacının tahmini ile gerçek sonuç arasında kaç gün fark vardır?
Çözüm: 2432 ÷ 32 = 76 gün. Gerçekte 76 günde boyayacaktır.
2432 m²’yi ve 76 günü en yakın yüzlüğe ve onluğa yuvarlayalım:
2432 → 2400
76 → 80
2400 ÷ 80 = 30 gün
Gerçek süre 32 gündü, tahmini süre 80 gün.
Fark: 32 – 30 = 2 gün
Tahmin ile gerçek sonuç arasında 2 gün fark vardır.

BÖLME İŞLEMİNDE KALAN YORUMLAMA

Bölme işlemi problemlerinde kalan probleme göre yorumlanmalıdır. Bir bölme işleminde kalan ihmal edilebilir.

Örnek: 80 tane bilyesi olan Ömer, bilyelerini 6 arkadaşına eşit şekilde paylaştıracaktır. Ömer’in arkadaşlarından her birine kaçar tane bilye düşeceğini bulalım.

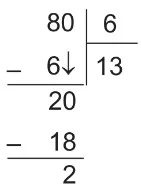
Ömer’in arkadaşlarından her birinin alacağı bilye sayısını bulmak için bilye sayısını arkadaş sayısına böleriz.
Bölüm (13) her birinin alacağı bilye sayısını verir.
Kalan (2) ise dağıtım yapıldıktan sonra Ömer’de kalan bilye sayısıdır.
Bu bilyeler eşit dağıtılamayacağından dolayı ihmal edilebilir.

Bir bölme işleminde kalan, bölüme yuvarlanabilir. Kalan 1 olarak bölüme ilave edilir.

Örnek: Bir toplantıdaki 128 kişi her biri beşer kişilik masalara oturacaktır. Bu toplantı için en az kaç tane masaya ihtiyaç olduğunu bulalım.

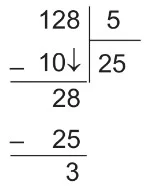
Masa sayısını bulmak için kişi sayısını 5’e böleriz.
25 masaya beşer kişi oturursa 125 kişi masalara oturmuş olur.
Kalan 3 kişi de bir masaya oturur.
Sonuç olarak 25 + 1 = 26 masaya ihtiyaç vardır.

Bir bölme işleminde kalan, kesir olarak ifade edilebilir.

Örnek: 25 tane çikolata 2 çocuğa paylaştırılıyor. Çocukların her birine ne kadar çikolata düşer?

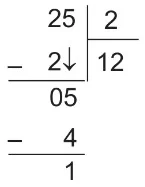
Her birine düşecek çikolata miktarını bulmak için çikolata sayısını çocuk sayısına böleriz.
Çocukların her birine 12 tane çikolata düşer, geriye 1 çikolata artar.
Artan çikolata da iki çocuğa yarım paylaştırılabilir.
Çocukların her birine 12 tam 1 yarım çikolata düşmüş olur.

Örnek: Bir okuldaki 285 öğrenci her biri 22 kişilik otobüslerle geziye götürülecektir. Bu gezi için en az kaç otobüse ihtiyaç vardır?
Çözüm: 285 ÷ 22 işlemi yapılır:
285 ÷ 22 = 12 (kalan 21)
Sonuç olarak 12 otobüs tam dolacaktır, ancak kalan 21 öğrenci için bir otobüs daha gerekmektedir.
12 + 1 = 13 otobüs gereklidir.

Örnek: Nurten 89 tane şekeri 7 arkadaşına her arkadaşında eşit sayıda şeker olacak şekilde paylaştıracaktır. Buna göre Nurten bir arkadaşına en fazla kaç şeker verebilir?
Çözüm: 89 ÷ 7 işlemi yapılır:
89 ÷ 7 = 12 (kalan 5)
Her bir arkadaşına en fazla 12 şeker düşecektir.

ÇARPMA VE BÖLME İŞLEMLERİNDE VERİLMEYENİ BULMA

Bir çarpma işleminde verilmeyen çarpanı bulmak için çarpım (sonuç) verilen çarpana bölünür.

Örnek: ⬛ × 18 = 162
162 ÷ 18 = 9
⬛ = 9

Örnek: 12 × ⬛ = 180
180 ÷ 12 = 15
⬛ = 15

Bir bölme işleminde bölünen, bölen ile bölümün çarpımına kalanın eklenmesiyle bulunur.

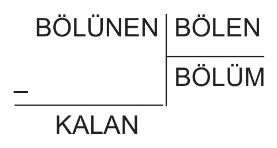
BÖLÜNEN = (BÖLEN × BÖLÜM) + KALAN

Örnek:

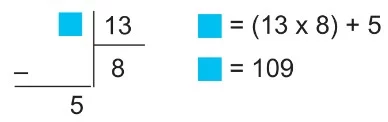
Örnek: ⬛ ÷ 7 = 26
26 × 7 = 182
⬛ = 182

Bir bölme işleminde bölen verilmediyse bölünenden kalan çıkarılır, elde edilen sayı bölüme bölünür.

Örnek:

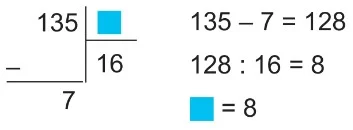
Örnek: 125 ÷ ⬛ = 5
⬛= 125 ÷ 5
⬛ = 25

Zühal öğretmen, öğrencilerinin her birine 230 soruluk test kitapçığı hazırlayacaktır. Her bir test kitapçığındaki sayfaları birbirine tutturtmak için 6 zımba teli kullanacaktır.

a: Zühal öğretmen, kitapçığı hazırlarken her sayfaya en fazla 12 soru koyarak hazırladığına göre bir kitapçık en az kaç sayfa olur?
Çözüm: Bir kitapçıkta toplam 230 soru vardır. Her sayfaya en fazla 12 soru koyabileceğimize göre, kitapçığın kaç sayfa olacağını bulmak için 230 sayısını 12’ye böleriz.
230 ÷ 12 = 19 (kalan 2)
Bu durumda, 19 sayfa tam olarak dolacaktır, ancak kalan 2 soru için bir sayfaya daha ihtiyaç vardır. Yani, toplamda en az 20 sayfa olur.

b. Zühal öğretmenin başlangıçta 250 zımba teli bulunduğuna göre kaç kitapçık hazırlayabilir?
Çözüm: Bir kitapçığı hazırlamak için 6 zımba teli gerekmektedir. Zühal öğretmenin elinde toplam 250 zımba teli bulunduğuna göre kaç kitapçık hazırlayabileceğini bulmak için 250 sayısını 6’ya böleriz.
250 ÷ 6 = 41 (kalan 4)
Bu durumda, Zühal öğretmen 41 tam kitapçık hazırlayabilir ve elinde 4 zımba teli artar. Yani, 41 kitapçık hazırlayabilir.

DOĞAL SAYI PROBLEMLERİ

Doğal sayılarla problem çözümlerinde aşağıda verilen adımlar takip edilebilir:

Problemin içerdiği sayı ve bileşenler belirlenir.
Problemde verilen ve istenenler arasındaki ilişki belirlenir.
Veriler uygun şekil, tablo ve grafik gibi matematiksel temsillere dönüştürülür.
Problem sonucuna ilişkin tahminde bulunularak işlemleri gerçekleştirme stratejileri belirlenir.
Belirlenen strateji uygulanır.
Çözüm yolları kontrol edilerek yeni stratejiler geliştirilir.
Kullanılan ve geliştirilen stratejiler gözden geçirilerek kısa yollar değerlendirilir.
Kullanılan ve geliştirilen stratejiler farklı problem çözümü için genellenir.
Genellemenin geçerliliği değerlendirilir.

Aşağıda verilen problemi yukarıda verilen problem çözme adımlarını kullanarak ayrıntılı bir şekilde inceleyelim.

Örnek: 7200 metre uzunluğundaki bir yolun başına ve sonuna dikilmek şartıyla eşit aralıklarla ağaç dikilecektir. Dikilecek ağaçlar arasındaki mesafenin en az 15 metre en fazla 18 metre olması gerekmektedir.

Buna göre aşağıda verilen soruları cevaplayınız.

a. Ağaçlar arasındaki mesafe metre cinsinden bir doğal sayıya eşit olduğuna göre dikilecek ağaç sayısının alabileceği değerleri bulunuz.

b. Kullanılacak ağaç sayısını en fazla kaç olabilir?

Problemde verilen ağaç dikilecek yolun uzunluğu 7200 metre ve ağaçlar arasındaki mesafenin alabileceği değerler verilmiştir.
Verilen bilgilere göre ağaçlar arasındaki mesafenin 7200’ü kalansız bölen değerler olması gerekir.
Ağaçlar arasındaki mesafe en az 15 metre en fazla 18 metre olacağından; 15, 16, 17 ve 18 sayılarından 7200 kalansız bölenleri belirlememiz gerekir.
Ağaçlar yolun başına ve sonuna dikileceği için kullanılan ağaç sayısı ağaçlar arasındaki boşluk sayısından 1 fazla olmalıdır.
Aşağıda verilen modelde görüldüğü gibi ağaçlar arasında üç boşluk varken dördüncü ağaç dikilmiştir.
7200 : 15 = 480 → 480 + 1 = 481
7200 : 16 = 450 → 450 + 1 = 451
7200 : 17 = Kalansız bölünemez.
7200 : 18 = 400 → 400 + 1 = 401
Kullanılacak ağaç sayısı en fazla 481 olabilir.
Kullanılacak ağaç sayısının fazla olmasını istersek ağaçlar arasındaki boşluğun en az, kullanılacak ağaç sayısının az olmasını istersek ağaçlar arasındaki boşluğun en fazla olması gerekir.
Dikilecek ağaç sayısı en az 401, en fazla 481 olur.
7200’ü tam bölemeyen 17, kullanılacak ağaç sayısını bulmamıza yardımcı olamaz.

Örnek: Satış için hazırlanan ürünler 16 tane kutuya her birinde 5’er tane olacak şekilde yerleştiriliyor. Sipariş veren müşterinin ürünleri her kutuda 8 tane olacak şekilde talep etmesi nedeniyle ürünler müşteri isteği doğrultusunda kutulanıyorlar.
Buna göre kullanılmadan artan kutu sayısı kaçtır?

Çözüm:

Toplam ürün sayısı: 16 tane kutuya her birine 5’er tane ürün yerleştirildiğine göre, toplamda 16 × 5 = 80 ürün bulunmaktadır.
Müşteri, her kutuda 8 tane ürün talep ediyor.

Şimdi, bu 80 ürünü, her kutuya 8 tane yerleştirerek kaç kutuya sığacağını bulalım:
80 ÷ 8 = 10 kutu
Bu durumda, toplamda 16 kutu vardı ama müşteri isteğine göre sadece 10 kutu kullanıldı.
Artan kutu sayısı: 16 – 10 = 6 kutu

ZAMAN ÖLÇME

Günlük yaşantımızda farklı zaman ölçü birimleri kullanılmaktadır. Zaman ölçü birimleriyle işlem yapabilmek için birimlerimizin birbiri ile aynı olması gerekir.
Zaman ölçü birimlerini birbirine dönüştürmek için aşağıda verilen eşitliklerden faydalanılır:
1 Yıl = 12 Ay
1 Ay = 30 Gün
1 Gün = 24 Saat
1 Saat = 60 Dakikadır.
Saat yerine “s”, dakika yerine ise “dk” kısaltmaları kullanılabilir.
Zaman ölçü birimleri ile toplama ve çıkarma işlemleri yapılırken küçük olan birim en sağda olacak şekilde küçükten büyüğe sağdan sola doğru birimler yazılır.

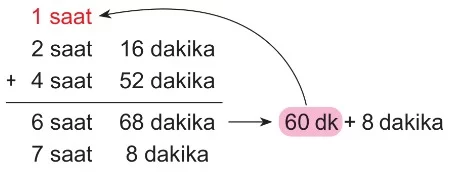
Örnek: Bir atölyede çalışan Serdar, 2 saat 16 dakika çalıştıktan sonra mola vermiş, ardından 4 saat 52 dakika çalıştıktan sonra işi bırakmıştır. Buna göre Serdar’ın çalışma süresinin kaç saat, kaç dakika olduğunu belirleyelim.

Çalışma süresini bulmak için verilen süreleri toplamalıyız.

Örnek: 113 dakika kaç saat kaç dakikaya eşittir?

Örnek: 38 ay kaç yıl kaç aya eşittir?

Örnek: Bir kafeteryada 3 ayaklı ve 4 ayaklı toplam 54 masa bulunmaktadır. Kafeteryadaki 4 ayaklı masaların sayısı, 3 ayaklı olanların sayısının 2 katına eşittir.
Buna göre kafeteryadaki masaların toplam ayak sayısı kaçtır?

Çözüm:

Şimdi, önce 3 ayaklı ve 4 ayaklı masaların kaç tane olduğunu anlamaya çalışalım. 3 ayaklı masaların sayısını bilmeden, 4 ayaklı masaların sayısının, 3 ayaklı olanların 2 katı olduğunu biliyoruz.

Bu durumda şöyle düşünebiliriz:

3 ayaklı masalardan bir grup varsa, 4 ayaklı masalardan 2 grup var.
Yani 3 ayaklı masalar 1 grup ve 4 ayaklı masalar 2 grup olduğuna göre, toplamda 3 grup masa var. Ve bu 3 grup masa toplamda 54 masa yapıyor.

54 masayı 3 gruba böldüğümüzde:
54 ÷ 3 = 18
Bu, 3 ayaklı masaların 18 tane olduğunu gösterir. 4 ayaklı masalar ise bunun 2 katı olduğuna göre:
18 × 2 = 36
Yani 4 ayaklı masalar 36 tanedir.
Şimdi, toplam ayak sayısını bulalım:

3 ayaklı masalardan: 18 masa × 3 ayak = 54 ayak
4 ayaklı masalardan: 36 masa × 4 ayak = 144 ayak

Toplam ayak sayısı:
54 + 144 = 198 ayak