Geometrik Cisimler

• 1. Konu: Dik Prizmaların Temel Elemanları ve Açınımı
• 2. Konu: Dik Dairesel Silindir, Yüzey Alanı ve Hacmi
• 3. Konu: Dik Piramidin Temel Elemanları ve Açınımı
• 4. Konu: Dik Koninin Temel Elemanları ve Açınımı

---

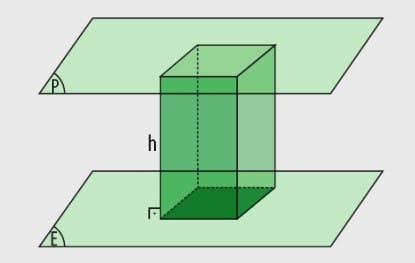
Aşağıda E ve P paralel düzlemlerdir. Bu düzlemler üzerindeki eş çokgenlerin karşılıklı köşeleri birleştirilerek elde edilen cisme prizma denir.Tabanlardaki karşılıklı köşeleri birleştiren ayrıtlar (yanal ayrıtlar) tabana dik ise bu prizmalara dik prizma, tabanlardaki karşılıklı köşeleri birleştiren ayrıtlar (yanal ayrıtlar) tabana dik değil ise bu prizmalara eğik prizma denir.

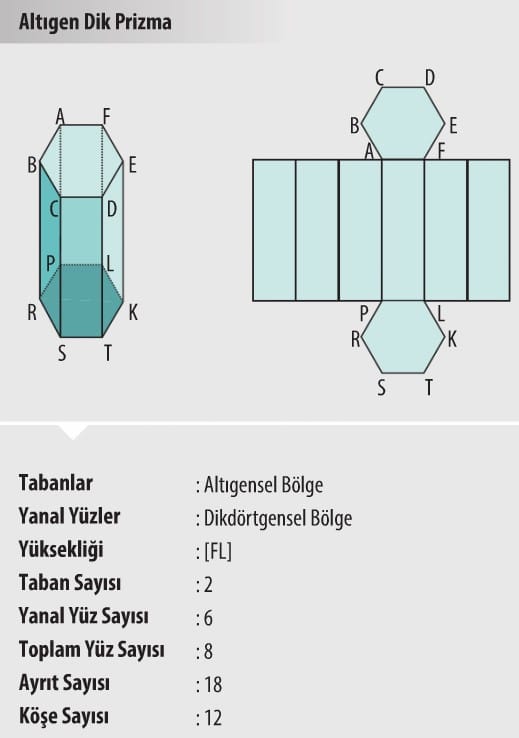
DİK PRİZMALAR

• Tüm prizmalar üç boyutlu şekillerdir.
• Prizmalarda tabanlar daima birbirine eş çokgensel bölgelerdir.
• Prizmaların tabanları arasındaki en kısa mesafe prizmanın yüksekliğidir.
• Prizmalarda yan yüzlerin veya yan yüzlerle tabanların kesiştiği kısımlara prizmanın ayrıtı denir.
• Prizmaların yan yüz ayrıtları birbirine paralel ve eşit uzunluktadır.
• Prizmalarda ayrıtların kesim noktaları köşeleri oluşturur.
• Prizmaların köşe sayısı, tabanını oluşturan çokgenin köşe sayısının 2 katıdır.
• Bir prizmanın köşe sayısı en az 6’dır.
• Dik prizmaların yanal ayrıtlarının uzunluğu, prizmanın yüksekliğine eşittir.
• Dik prizmanın yanal yüzleri dikdörtgensel bölgelerdir.
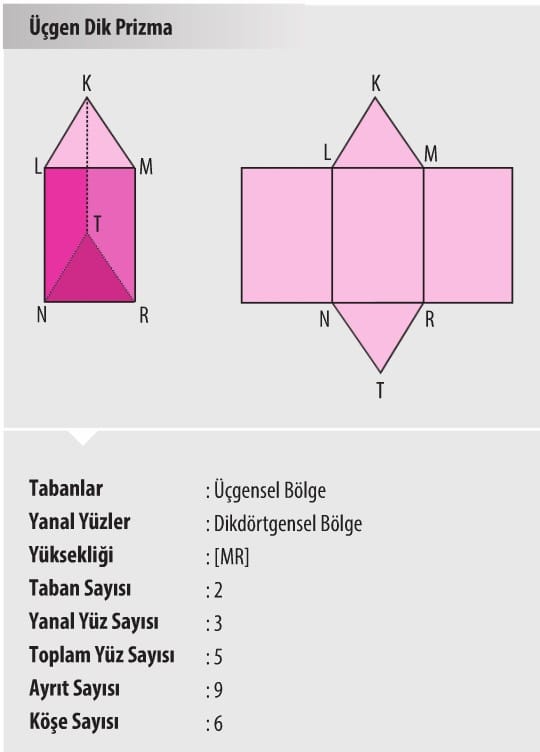
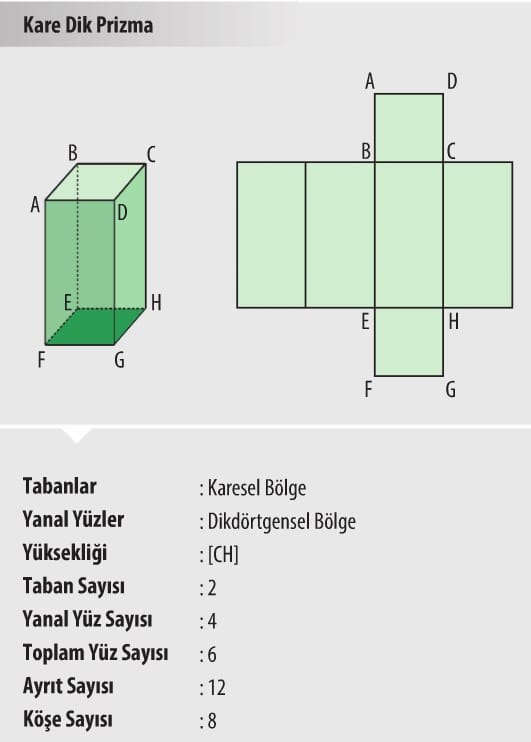
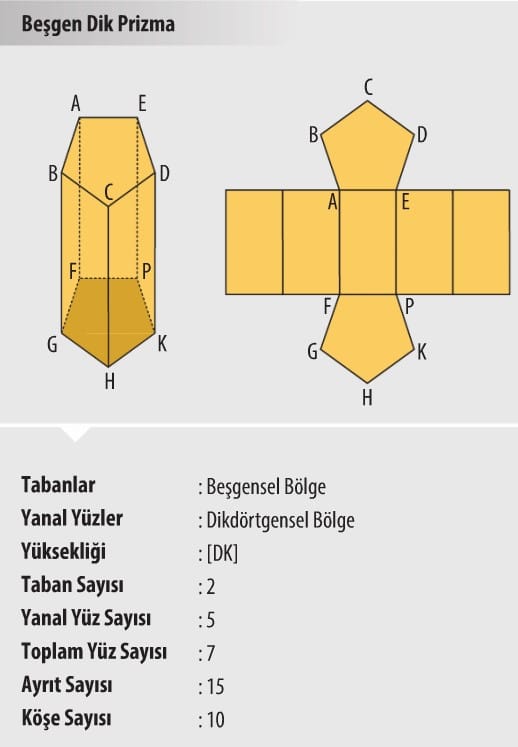
• Prizmalar tabanlarını oluşturan çokgenin ismine göre isimlendirilir. Örneğin dik prizmalardan tabanı kare şeklinde olan prizmalar kare dik prizma, tabanı üçgen olan dik prizma üçgen dik prizma şeklinde İsimlendirilir.
• Dik prizmaların temel elemanları taban, yan yüz, ayrıt, köşe ve yüksekliktir.

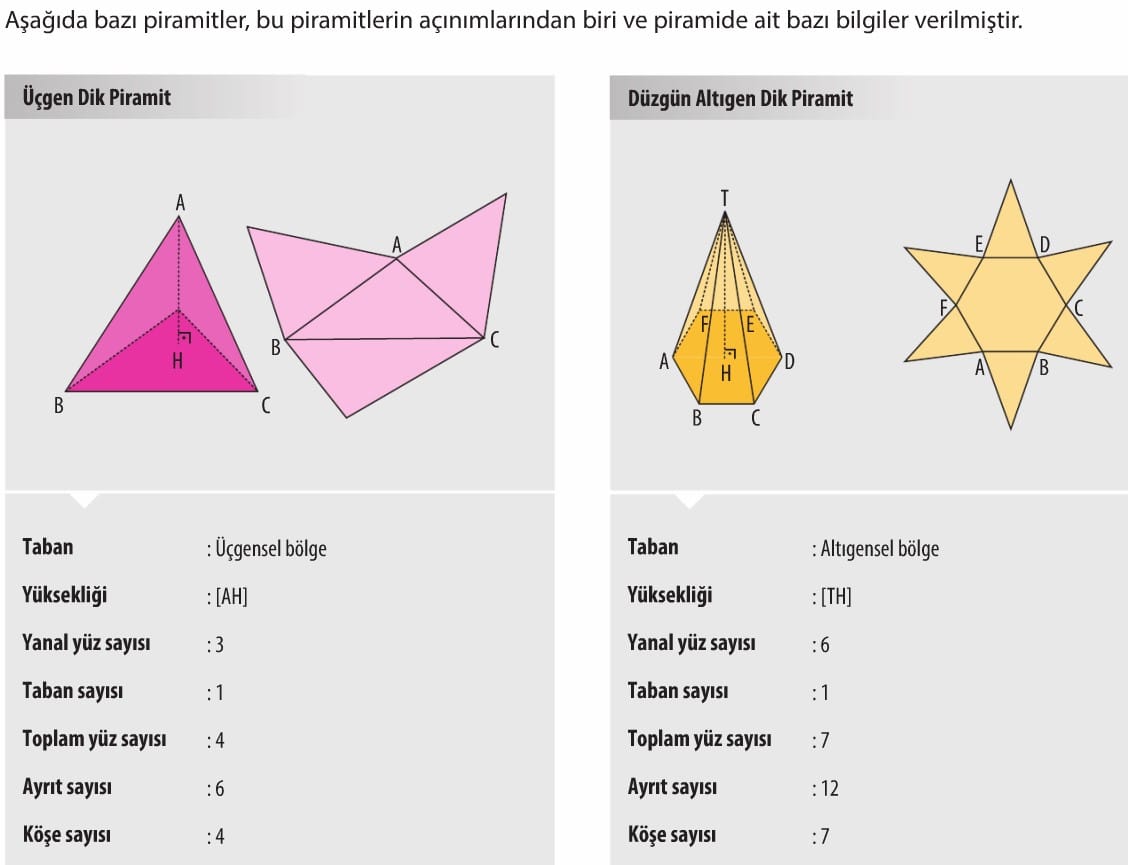
Aşağıda bazı prizmalar, bu prizmaların açılımlarından biri ve prizmaya ait bazı bilgiler verilmiştir.

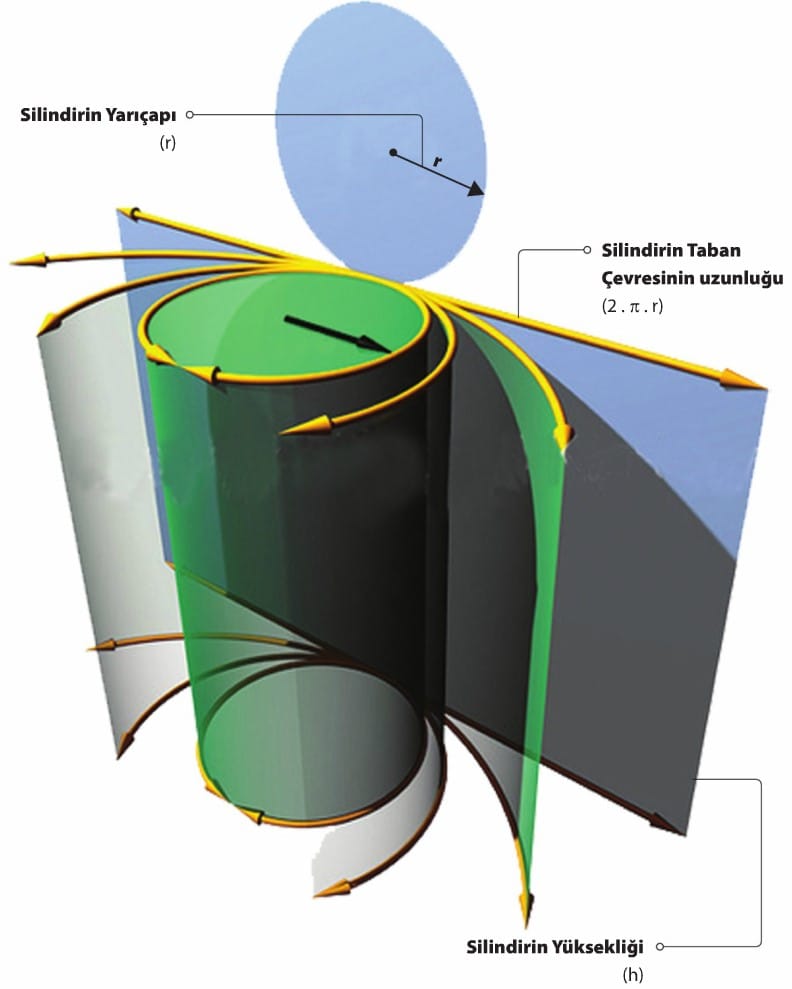
DİK DAİRESEL SİLİNDİR

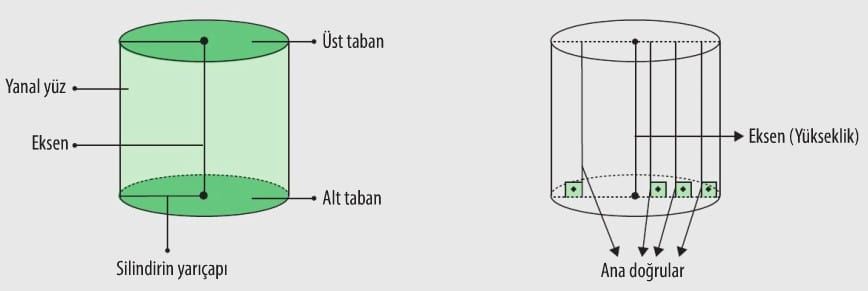
Dairesel silindir, birbirine eş ve paralel iki daire olan tabanlar ile bir yanal yüzden oluşmaktadır. Bu silindirde tabanların merkezlerini birleştiren doğruya eksen denir.Tabanların karşılıklı iki noktasını birleştiren ve eksene paralel olan doğrulara ise silindirin ana doğruları veya doğuranları denir.

Tabanlardan birinin bir noktasından, diğer tabanın düzlemine inilen dikme, silindirin yüksekliği, taban yarıçapı da silindirin yarıçapıdır. Dairesel silindirin ekseni tabanlara dik ise silindir dik dairesel silindir olarak adlandırılmaktadır. Dairesel silindirin temel elemanları taban, yan yüz, yükseklik ve ana doğrudur. Aşağıdaki şekilde bir dik dairesel silindir, ekseni ve ana doğruları verilmiştir.

Dik dairesel silindirde eksen ile ana doğrular aynı zamanda silindirin yüksekliğidir. Dairesel silindirin ekseni tabanlara dik değilse silindir eğik dairesel silindir olarak adlandırılmaktadır. Aşağıdaki şekilde bir eğik dairesel silindir, ekseni, yüksekliği ve ana doğruları verilmiştir.

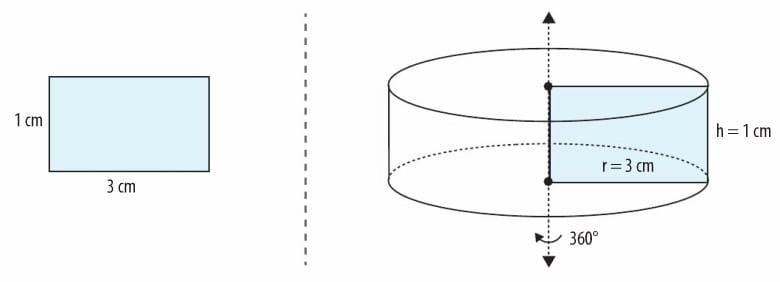
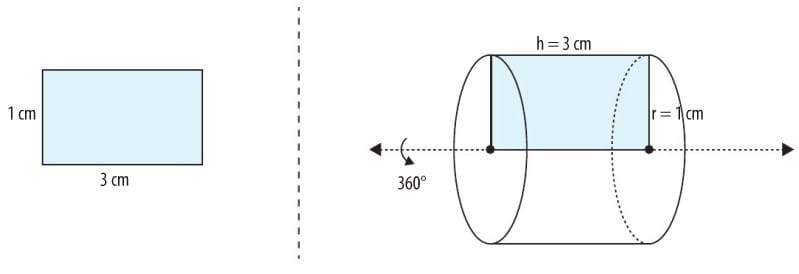
Bilgi: Bir dikdörtgensel bölge bir kenarı etrafında 360⁰ döndürüldüğünde dik dairesel silindir oluşur. Hangi kenarı etrafında döndürülüyorsa o kenar dik dairesel silindirin yüksekliği, diğer kenar da dik dairesel silindirin yarıçapıdır.

Verilen dikdörtgensel bölge kısa kenarı etrafında 360° döndürüldüğünde yarıçapının uzunluğu 3 cm, yüksekliği 1 cm olan dik dairesel silindir oluşur.

Verilen dikdörtgensel bölge uzun kenarı etrafında 360” döndürüldüğünde yarıçapının uzunluğu 1 cm, yüksekliği 3 cm olan dik dairesel silindir oluşur.

Dik dairesel silindirin açılımında yanal yüz bir dikdörtgensel (veya karesel) bölge ve tabanlar da birer dairedir.

Görüldüğü gibi yanal yüzün kenarlarından birinin uzunluğu silindirin taban çevresinin uzunluğuna, diğerinin uzunluğu silindirin yüksekliğine eşittir. Silindirin açılımında tabanlar birbirine eş dairelerdir.

DİK DAİRESEL SİLİNDİRİN YÜZEY ALANI

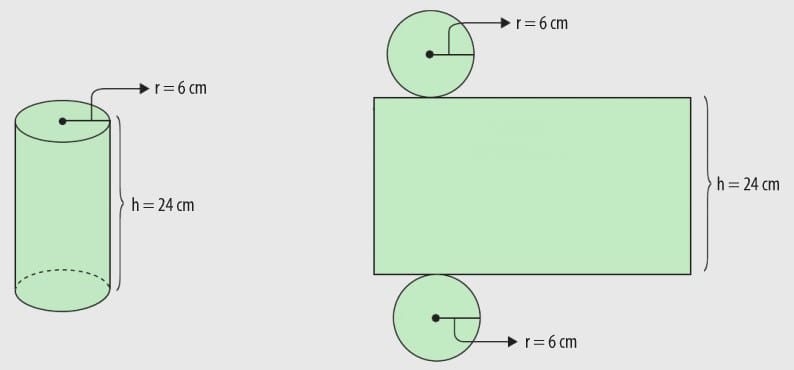
Bir gıda fabrikası, yeni çıkarttığı bir lokum çeşidini, dik dairesel silindir biçimindeki plastik kutularda satacaktır. Bu kutulardan bir tanesinin yarıçap uzunluğu 6 cm ve yüksekliği 24 cm olacağına göre, bu gıda fabrikasının bir plastik kutu için kaç cm² lik plastik kullanacağını π yi 3 alarak bulalım.

Bir kutu için kullanılacak plastik miktarını bulmak için, dik dairesel silindir biçimindeki bir kutunun yüzey alanını bulmalıyız. Önce bir kutunun ölçülerini belirterek açılımını çizelim. Açılımda tabanlar daire, yanal yüz ise dikdörtgensel bölgedir.

Bu plastik kutunun alanını bulmak için dikdörtgenin alanı ile iki dairenin alanlarını bulup toplamalıyız. Bir dairenin alanı π . r² olduğundan, iki eş dairenin alanları toplamı;

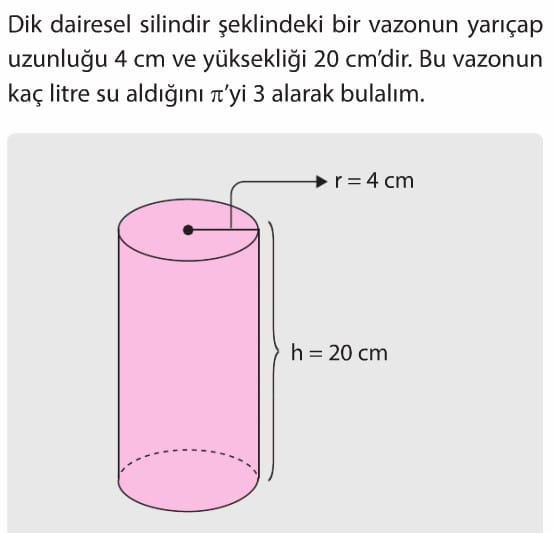
DİK DAİRESEL SİLİNDİRİN HACMİ

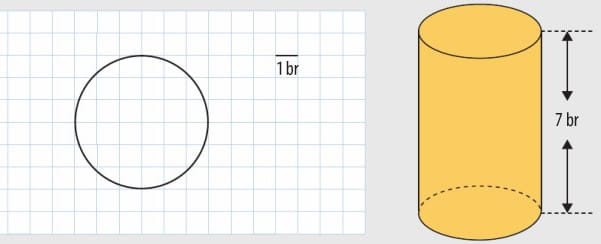
Aşağıda kareli kâğıtta yüksekliği 7 br olan dik silindirin taban dairesi verilmiştir. Bu silindirin hacmini tahmin edelim.

Silindirin tabanı 16 tam, 20 tam olmayan birim karelerden oluştuğundan 20 tam olmayan birim kareyi 10 tam birim kare olarak alabiliriz. Bu durumda tabanın alanı tahmini olarak,

16+ 10 = 26 br² olur.

Bu şekilde silindirin tabanına ayrıt uzunluğu 1 br olan birim küplerden bir sıra dizildiğinde oluşan hacim tahmini olarak 26 br³ olur.

Silindirin yüksekliği 7 br olduğundan, silindirin içine üst üste bir ayrıt uzunluğu 1 br olan 7 sıra birim küp yerleştirilebilir. Bu durumda silindirin tahmini hacmi, 26 . 7 = 182 br³ olur.

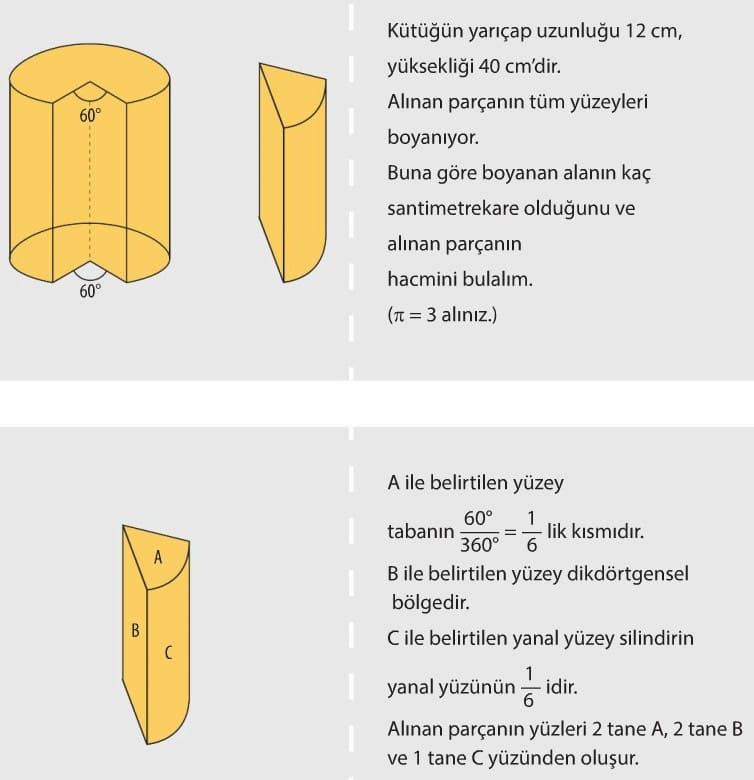
Silindir şeklindeki bir kütüğün taban dairelerinden karşılıklı olarak 60⁰ lik kısımları işaretlenerek kütükten şekildeki gibi bir parça alınıyor.

DİK PİRAMİT

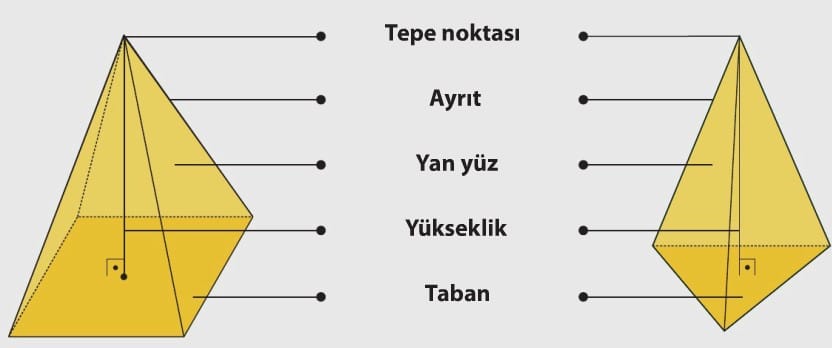
Piramitler tabanını oluşturan çokgene göre İsimlendirilir. Piramidin temel elemanları tepe noktası, tabanı, yan yüzleri, ayrıtları ve yüksekliğidir. Piramitte yükseklik tepenin taban düzlemine olan uzaklığıdır. Piramidin tepe noktasını taban merkezine (ağırlık merkezi) birleştiren doğru parçası tabana dik ise dik piramit, eğik ise eğik piramit olarak adlandırılır. Aşağıdaki şekilde bir kare dik piramit ve bir üçgen dik piramit üzerinde bazı kısımlar belirtilmiştir.

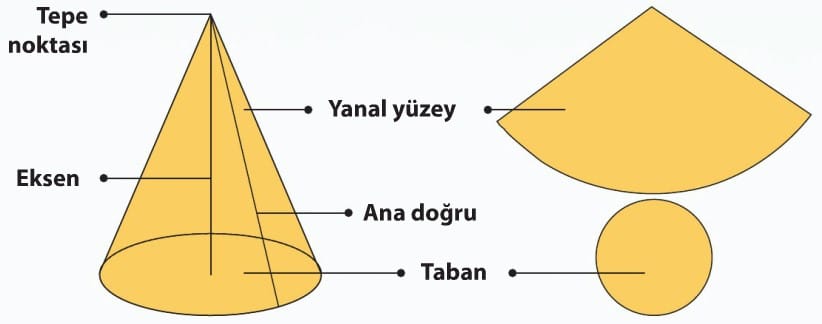
Dik Koni

Koni, tabanını oluşturan bir daire ve yan yüzünü oluşturan bir daire diliminden oluşur. Ekseni tabana dik olan koni dik koni veya dönel koni, eğik olan ise eğik koni olarak adlandırılır. Koninin temel elemanları, bir dairesel bölge olan “taban”, tabanın dışında bir “tepe noktası”, tepe noktasını taban merkezine birleştiren doğru parçası olan “eksen”, tepeden geçen ve tabanın kenarı olan çembere dayanan “ana doğru (doğuran)” ve bu doğrunun süpürdüğü “yanal yüzey”dir. Dik konide eksen aynı zamanda koninin yüksekliğidir.