Dik Dairesel Silindir 8. Sınıf
Tabanları birbirine eş ve paralel iki daireden oluşan geometrik cisme silindir denir. Silindire bir varili örnek olarak verebiliriz.
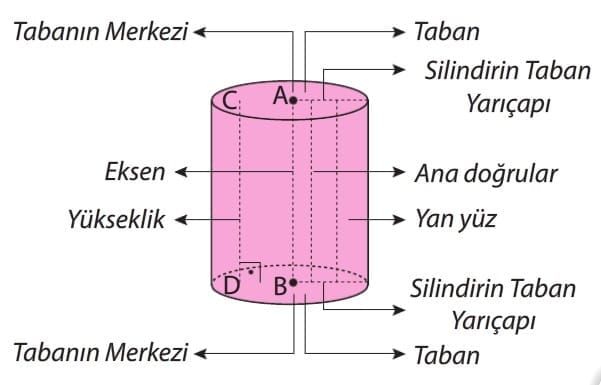
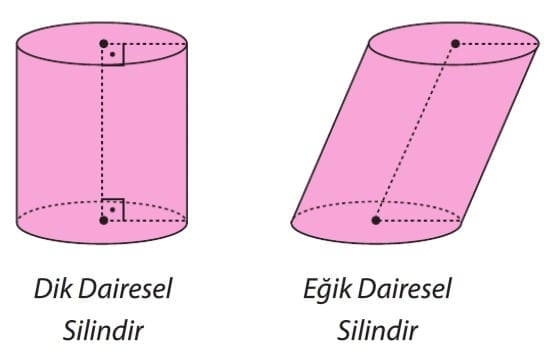
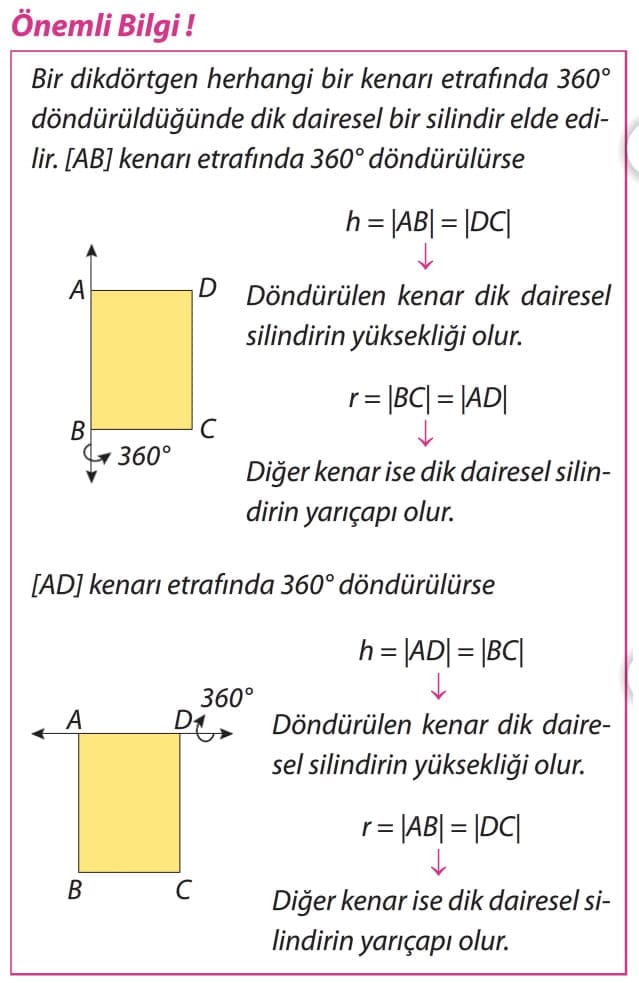
Dairesel silindirde tabanların merkezini birleştiren doğru parçasına eksen denir. Tabanların herhangi bir noktasını birleştiren ve tabanlara dik olan doğru silindirin yüksekliğidir. Tabanların karşılıklı iki noktasını birleştiren ve silindirin eksenine paralel olan doğrulara silindirin ana doğruları denir. Silindirin ekseni tabanlara dik ise silindire dik dairesel silindir, dik değilse eğik dairesel silindir denir.
Dikkat: Bir silindirin tabanı daire olduğundan taban çevresi 2πr, taban alanı πr2 ile bulunur. Silindirin temel elamanları tabanlar, yan yüz, eksen, ana doğrular ve yüksekliktir.
A. DİK DAİRESEL SİLİNDİRİN AÇINIMI
Dik dairesel silindirin açınımında tabanları oluşturan daireler ile yan yüzü oluşturan dikdörtgen bulunur.
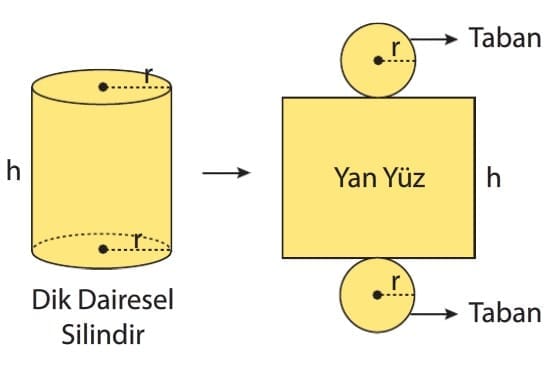
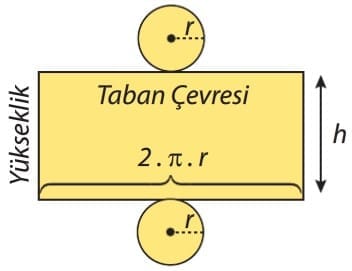
Önemli Bilgi: Yan yüzü oluşturan dikdörtgenin bir kenar uzunluğu dik dairesel silindirin yüksekliğine, diğer kenar uzunluğu ise dik dairesel silindirin taban çevresine eşittir.
Yükseklik = h
Taban Çevresi = 2. π . r
B. DİK DAİRESEL SİLİNDİRİN YÜZEY ALANI
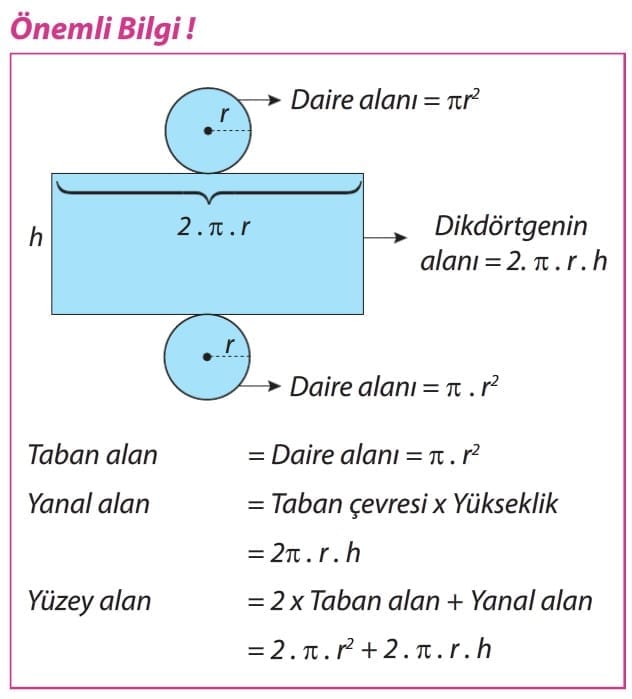
Dik dairesel silindirin alanı hesaplanırken açınımından faydalanılır.
C. DİK DAİRESEL SİLİNDİRİN HACMİ
Dik dairesel silindirin hacmini hesaplamak için dik dairesel silindirin taban alanını ve yüksekliğini kullanırız.
Dik Dairesel Silindir Yüzey Alanı ve Hacmi 8. Sınıf konu anlatımı Lgs çözümlü sorular
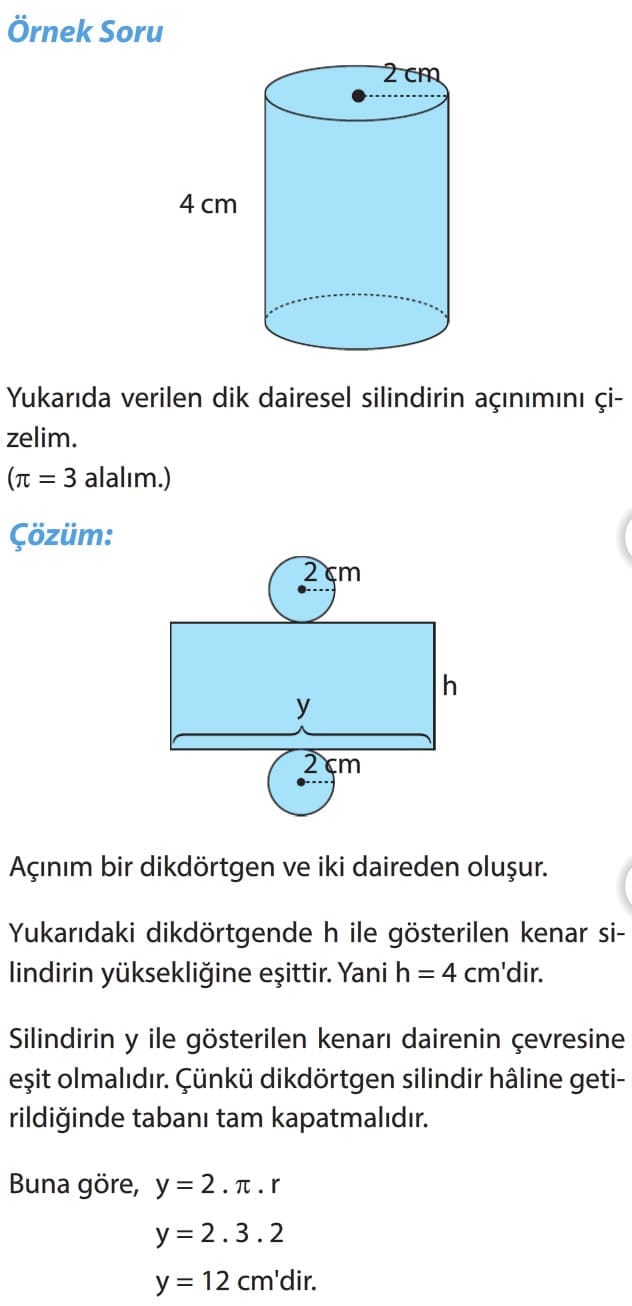
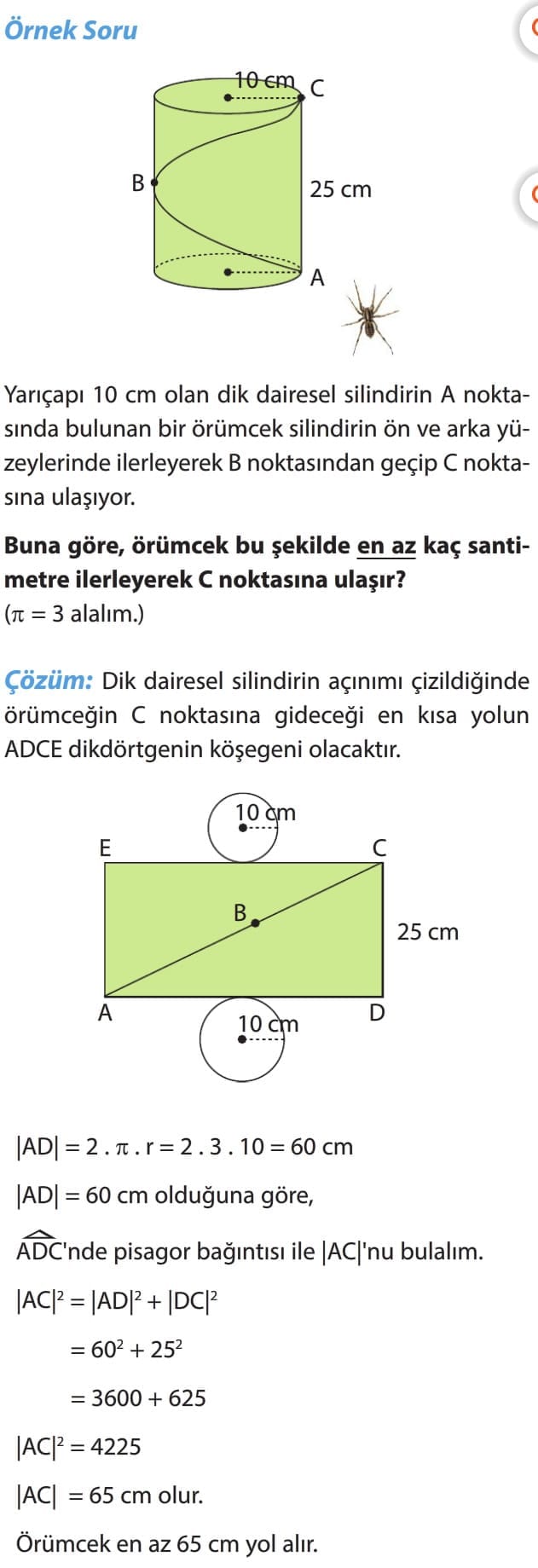
Örnek Soru: Yukarıda verilen dik dairesel silindirin açınımını çizelim. (pi = 3 alalım.)
Çözüm: Açınım bir dikdörtgen ve iki daireden oluşur. Yukarıdaki dikdörtgende h ile gösterilen kenar silindirin yüksekliğine eşittir. Yani h = 4 cm'dir. Silindirin y ile gösterilen kenarı dairenin çevresine eşit olmalıdır. Çünkü dikdörtgen silindir hâline getirildiğinde tabanı tam kapatmalıdır. Buna göre, y=2 . pi . r
y = 2.3.2
y = 12 cm'dir.
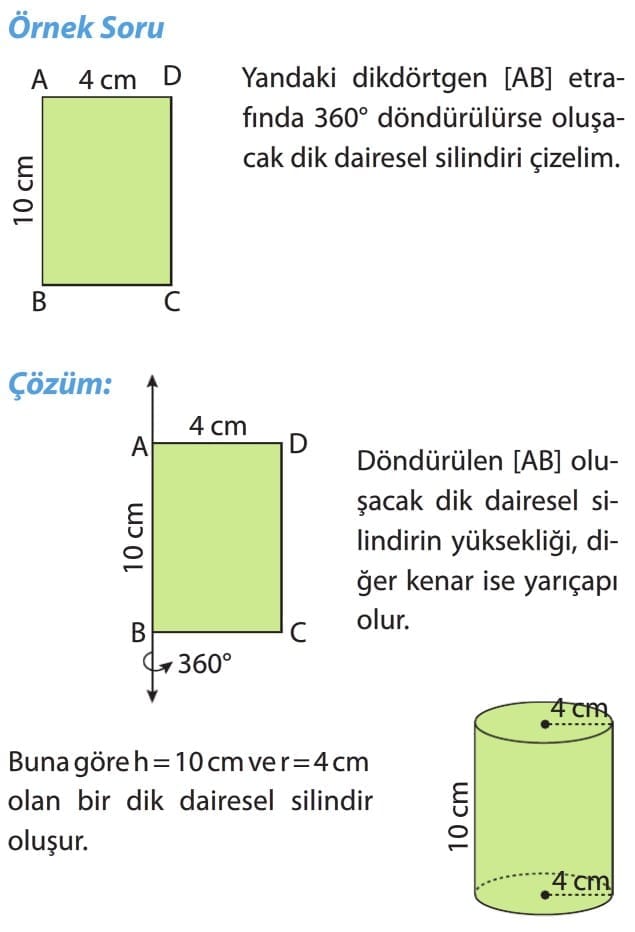
Örnek Soru: Yan yüzeyinin açınımı ABCD karesi olan bir dik dairesel silindirin yarıçapı kaç santimetre olur? (pi = 3 alalım.)
Çözüm: Karenin bir kenar uzunluğu dik dairesel silindirin taban çevresine eşittir.
Buna göre, 2 . pi . r =42
2.3 .r = 42
6. r = 42
r = 7 cm bulunur.
Silindirin taban yarıçapı 7 cm ve yüksekliği 42 cm'dir.
Soru: Yukarıdaki dikdörtgenler prizması şeklinde verilen homojen metal levhadan, dört farklı silindir şeklinde içi boş olan 4 cm yüksekliğindeki borular kesilip çıkartılacaktır. Verilen bilgilere göre, kesilip çıkartılan borularda kullanılan metallerin hacim sıralaması nasıl olmalıdır?
Soru: Bir zeytinyağı fabrikası için yüksekliği 40 cm ve taban çevresi 60 cm olan dik dairesel silindir şeklinde teneke kutular hazırlanmaktadır. Bu teneke kutuların yan yüzleri ve tabanları tek parçadan oluşacak şekildedir. Bir kenar uzunluğu 2 metre olan kare şeklindeki bir teneke levhadan en fazla kaç tane dik dairesel silindir şeklinde kutu elde edilebilir? (n = 3 alalım.)
A) 11 B) 12 C) 13 D) 14