Bunlarda İşinize Yarayabilir

• Çarpanlar ve Katlar Ders Notları
• Çarpanlar ve Katlar Testleri

Çarpanlar ve Katlar Çözümlü Sorular

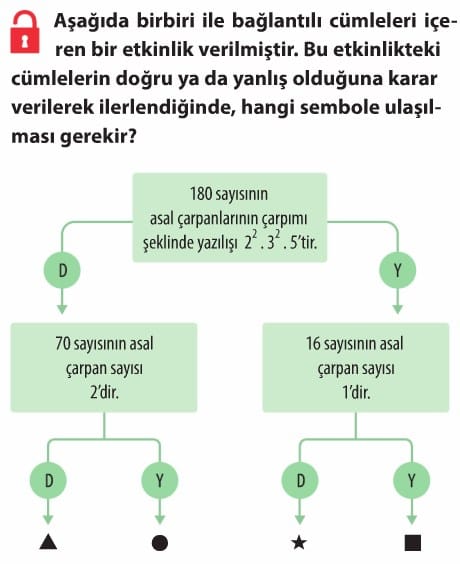
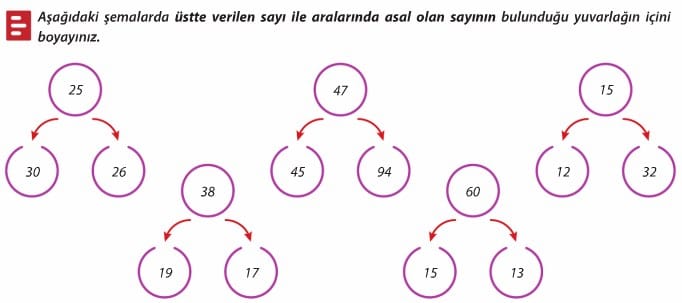
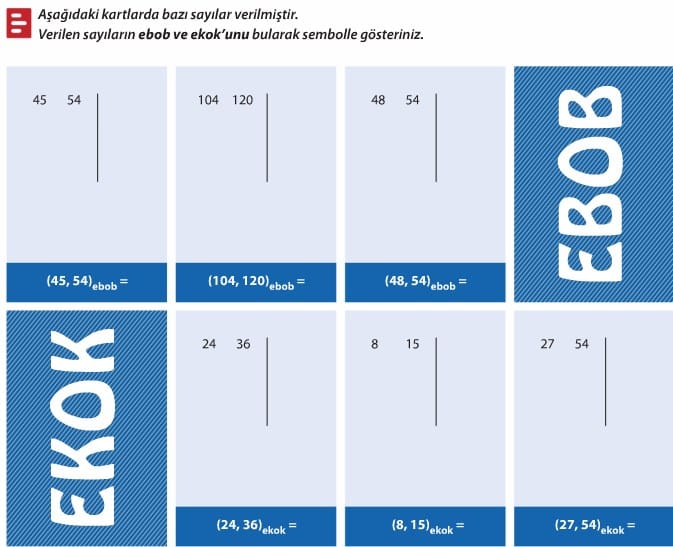
Çarpanlar ve Katlar Etkinlikler

Çözümlü Örnek Test Soruları: Çarpanlar ve Katlar

Soru 1: 36 sayısının asal çarpanlarına ayrılmış hali aşağıdakilerden hangisidir?
A) 2² × 3
B) 2³ × 3
C) 2² × 3²
D) 2 × 3²
Cevap: C
Çözüm: 36 sayısını asal çarpanlarına ayırdığımızda 36 = 2 × 2 × 3 × 3 = 2² × 3² olur.

Soru 2: 48 ve 60 sayılarının EBOB’u kaçtır?
A) 6
B) 8
C) 12
D) 24
Cevap: C
Çözüm: 48 ve 60 sayılarının ortak bölenlerini bulalım. En büyük ortak bölen (EBOB) 12’dir.

Soru 3: 24 ve 36 sayılarının EKOK’u kaçtır?
A) 72
B) 48
C) 144
D) 96
Cevap: A
Çözüm: 24 ve 36 sayılarının en küçük ortak katı (EKOK) 72’dir.

Soru 4: 12, 18 ve 30 sayılarının ortak bölenlerinin en büyüğü kaçtır?
A) 2
B) 3
C) 6
D) 12
Cevap: C
Çözüm: 12, 18 ve 30 sayılarının ortak bölenleri arasındaki en büyük sayı 6’dır.

Soru 5: 45 sayısının asal çarpanlarının toplamı kaçtır?
A) 8
B) 10
C) 12
D) 14
Cevap: B
Çözüm: 45 sayısının asal çarpanları 3 ve 5’tir. 3 + 5 = 8.

Soru 6: 40 ve 64 sayılarının EBOB’u ve EKOK’u sırasıyla kaçtır?
A) 8 ve 320
B) 4 ve 160
C) 8 ve 160
D) 16 ve 320
Cevap: C
Çözüm: 40 ve 64 sayılarının EBOB’u 8, EKOK’u ise 160’tır.

Soru 7: 54 sayısının asal çarpanlarına ayrılışı aşağıdakilerden hangisidir?
A) 2 × 3³
B) 2 × 3²
C) 3 × 3³
D) 2² × 3
Cevap: A
Çözüm: 54 sayısını asal çarpanlarına ayırdığımızda 54 = 2 × 3 × 3 × 3 = 2 × 3³ olur.

Soru 8: 18 ve 24 sayılarının en büyük ortak böleni kaçtır?
A) 3
B) 4
C) 6
D) 12
Cevap: D
Çözüm: 18 ve 24 sayılarının ortak bölenleri arasındaki en büyük sayı 12’dir.

Soru 9: 14 ve 21 sayılarının en küçük ortak katı (EKOK) kaçtır?
A) 14
B) 21
C) 28
D) 42
Cevap: D
Çözüm: 14 ve 21’in en küçük ortak katı 42’dir.

Soru 10: 32 ve 48 sayılarının asal çarpanları nelerdir?
A) Sadece 2
B) Sadece 3
C) 2 ve 3
D) 2 ve 5
Cevap: A
Çözüm: 32 ve 48 sayılarının asal çarpanlarına bakıldığında her ikisi de yalnızca 2’ye bölünebilir.

---

Soru 1:
36 ve 48 sayılarının en büyük ortak böleni (EBOB) nedir?

Çözüm:
İlk adım olarak, 36 ve 48 sayılarının asal çarpanlarını bulalım:

36 = 2² × 3²
48 = 2⁴ × 3

Bu iki sayının ortak asal çarpanları 2 ve 3’tür. Şimdi bu çarpanların en küçük üslerini alarak EBOB’u bulalım:

EBOB(36, 48) = 2² × 3 = 4 × 3 = 12

Cevap: 36 ve 48 sayılarının EBOB’u 12’dir.

Soru 2:
12 ve 18 sayılarının en küçük ortak katı (EKOK) nedir?

Çözüm:
İlk olarak, 12 ve 18 sayılarının asal çarpanlarını bulalım:

12 = 2² × 3
18 = 2 × 3²

Bu iki sayının asal çarpanlarının en büyük üslerini alarak EKOK’u hesaplayalım:

EKOK(12, 18) = 2² × 3² = 4 × 9 = 36

Cevap: 12 ve 18 sayılarının EKOK’u 36’dır.

Soru 3:
24 ve 36 sayılarının hem EBOB’unu hem de EKOK’unu bulun.

Çözüm:
İlk olarak asal çarpanları bulalım:

24 = 2³ × 3
36 = 2² × 3²

• EBOB: Ortak çarpanların en küçük üslerini alıyoruz:
  EBOB(24, 36) = 2² × 3 = 4 × 3 = 12
• EKOK: Ortak çarpanların en büyük üslerini alıyoruz:
  EKOK(24, 36) = 2³ × 3² = 8 × 9 = 72

Cevap: 24 ve 36 sayılarının EBOB’u 12, EKOK’u 72’dir.

Soru 4:
16, 24 ve 40 sayılarının EBOB’u nedir?

Çözüm:
İlk olarak asal çarpanlarını bulalım:

16 = 2⁴
24 = 2³ × 3
40 = 2³ × 5

Ortak asal çarpan sadece 2’dir ve ortak çarpanın en küçük üssünü alıyoruz:

EBOB(16, 24, 40) = 2³ = 8

Cevap: 16, 24 ve 40 sayılarının EBOB’u 8’dir.

Soru 5: 48 sayısının tüm çarpanlarını bulun.

Çözüm:
48 sayısının çarpanlarını bulmak için asal çarpanlarını yazalım:
48 = 2⁴ × 3

Bu asal çarpanlardan hareketle tüm çarpanlar şunlardır:

1, 2, 3, 4, 6, 8, 12, 16, 24, 48

Cevap: 48 sayısının çarpanları: 1, 2, 3, 4, 6, 8, 12, 16, 24 ve 48’dir.

Soru 6: Bir sınıftaki öğrenciler, sıra şeklinde ya 6’lı ya da 8’li gruplar halinde dizildiğinde, her iki durumda da tam olarak diziliyor. Bu sınıftaki en az kaç öğrenci olabilir?

Çözüm:
Soruda istenen, 6 ve 8 sayılarının en küçük ortak katını (EKOK) bulmaktır:

6 = 2 × 3
8 = 2³

En büyük üsleri alarak EKOK’u hesaplayalım:
EKOK(6, 8) = 2³ × 3 = 24

Cevap: Sınıftaki en az öğrenci sayısı 24’tür.