Gerçek sayılar, matematikte önemli bir yer tutan ve günlük hayatta da sıkça karşılaşılan sayılardır. Gerçek sayı kümesi, rasyonel ve irrasyonel sayıları kapsayan en geniş kümedir ve R sembolü ile gösterilir. Gerçek sayıların üzerinde aralıklar tanımlanarak çeşitli işlemler yapılabilir. Bu ders notunda, gerçek sayı aralıkları ve bu aralıklar üzerinde yapılan işlemleri detaylıca inceleyeceğiz.

Bu yazımızda Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler konu anlatımı yer almaktadır. Konu anlatımını bitirdikten aşağıdaki bağlantıya tıklayarak konu ile ilgili test soruları çözebilirsiniz.
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Testleri

Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Ders Notu (Yeni Müfredat)

Aralıkların Gösterimi

• a sayısı b sayısına eşit ise “a = b“, eşit değilse “a ≠ b” biçiminde yazılır.
• a > b (a büyüktür b’den)
• a < b (a küçüktür b’den) olmak üzere iki durum vardır.
• Sayı doğrusunda herhangi bir sayının sağında bulunan sayılar daima o sayıdan büyük, solunda bulunan sayılar daima o sayıdan küçüktür.
• a < x < b ise,

x, a ile b arasında olup sınır değerlerini alamaz ve x ∈ (a, b) ya da A = {x| a < x < b, x ∈ R} ile gösterilir.
(a, b) aralığına açık aralık denir.

• a ≤ x ≤ b ise,

x, a ile b arasında olup sınır değerlerini alabilir ve x ∈ [a, b] ya da A = {x| a ≤ x ≤ b, x ∈ R} gösterilir.
[a, b] aralığına kapalı aralık denir.

• a < x ≤ b ise,

x, a ile b arasında olup b değerini alabilirken a değerini alamaz. x ∈ (a, b] ya da A = {x| a < x ≤ b, x ∈ R} ile gösterilir.
(a, b] aralığına yarı açık aralık denir.

• a ≤ x < b ise,

x, a ile b arasında olup a değerini alabilirken b değerini alamaz. x ∈ [a, b) ya da A = {x| a ≤ x < b, x ∈ R} ile gösterilir.
[a, b) aralığına yarı açık aralık denir.

Gerçek Sayı Aralıklarında İşlemler

Gerçek sayı aralıkları arasında işlem yaparken küme kavramında kullandığımız sembollerden yararlanırız.

Örneğin:
A = {x| −3 < x ≤ 2, x ∈ R}
B = {x| −1 ≤ x < 4, x ∈ R} kümeleri verilsin.

x ∈ R olmak üzere, A kümesi (−3, 2] ve B kümesi [−1, 4) aralığı biçiminde gösterilebilir.

Bu durumda:

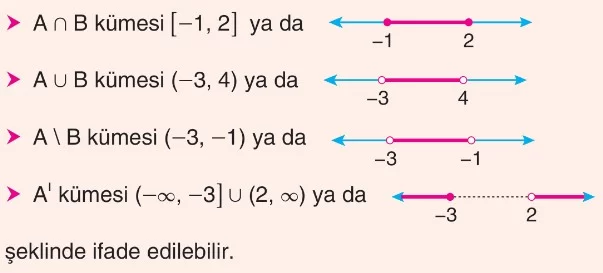
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Çözümlü Sorular

Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Testleri

Çözümlü Test Soruları

1. Aşağıdaki ifadelerden hangisi (-3, 5] aralığını doğru şekilde tanımlar?
A) -3 < x ≤ 5
B) -3 ≤ x < 5
C) -3 ≤ x ≤ 5
D) -3 < x < 5

Çözüm:
(-3, 5] aralığı -3 hariç, 5 dahil tüm sayıları içerir.
Cevap: A) -3 < x ≤ 5

———————————————————————————

2. [2, 7) ∩ (5, 9] aralığının sonucu nedir?
A) (5, 7)
B) [5, 7]
C) (5, 7]
D) [5, 7)

Çözüm:
∩ (kesişim) işlemi için ortak aralık bulunur:
[2,7) ve (5,9] → (5,7)
Cevap: A) (5, 7)

———————————————————————————

3. (-∞, 4) ∪ [2, 6] ifadesinin eşiti nedir?
A) (-∞, 6]
B) (-∞, 4)
C) [2, 6]
D) (-∞, 6)

Çözüm:
∪ (birleşim) işlemi için tüm elemanlar alınır:
(-∞,4) ve [2,6] → (-∞,6]
Cevap: A) (-∞, 6]

———————————————————————————

4. x ∈ [-1, 3) olmak üzere |x-1| < 2 eşitsizliğinin çözüm kümesi nedir?
A) [0, 2]
B) (-1, 3)
C) (0, 3)
D) [-1, 3)

Çözüm:
|x-1| < 2 → -2 < x-1 < 2 → -1 < x < 3
[-1,3) aralığıyla kesişimi: (-1,3)
Cevap: B) (-1, 3)

———————————————————————————

5. A = (2, 5] ve B = [4, 7) olduğuna göre A\B fark kümesi nedir?
A) (2, 4)
B) (2, 4]
C) [4, 5]
D) (5, 7)

Çözüm:
A\B = A’da olup B’de olmayan elemanlar:
(2,5] – [4,7) = (2,4)
Cevap: A) (2, 4)

———————————————————————————

6. (1, 4] × [-2, 3) kartezyen çarpımının grafiği için aşağıdakilerden hangisi doğrudur?
A) x=1 ve y=3 doğruları dahil değildir
B) x=4 ve y=-2 doğruları dahildir
C) x=1 ve y=-2 doğruları dahil değildir
D) x=4 ve y=3 doğruları dahildir

Çözüm:
(1,4] → x=1 hariç, x=4 dahil
[-2,3) → y=-2 dahil, y=3 hariç
Cevap: C) x=1 ve y=-2 doğruları dahil değildir

---

Sayı doğrusu üzerinde birbirinden farklı iki noktanın arasındaki tüm gerçek sayılardan oluşan alt kümeye aralık adı verilir. Aralıklar verilen kümeye uç noktalarının dahil edilip edilmemesine bağlı olarak adlandırılır. Aralık gösterimi [a,b], (a,b), [a,b), (a,b] ifadeleri kullanılarak yapılır. Bu gösterimlerdeki a ve b gerçek sayıları birer uç noktadır.

Kapalı Aralık: a, b, x ∈ R ve a < b olsun. Uç noktaların (a ve b nin) aralığa dahil olduğu kümeler a ≤ x ≤ b kapalı aralık olarak adlandırılır ve [a, b] şeklinde gösterilir.

Açık Aralık: Uç noktaların (a ve b nin) aralığa dahil olmadığı kümeler a < x < b açık aralık olarak adlandırılır ve (a, b) şeklinde gösterilir.

Yarı Açık Aralık: a, b, x ∈ R ve a< b olsun. Uç noktalardan birinin aralığa dahil olmadığı kümeler (a < x ≤ b ya da a ≤ x < b) yarı açık aralık olarak adlandırılır ve (a, b] ya da [a, b) şeklinde gösterilir. (-∞, +∞) aralığı ile gerçek sayılar kümesi ifade edilir. Diğer bir ifadeyle, R = (-∞, +∞) olur.

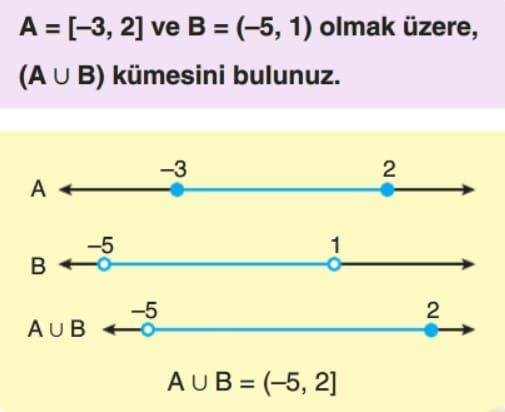
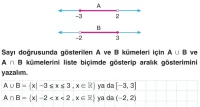
Gerçek sayı aralıkları ve bu aralıklar üzerinde yapılan işlemler, matematiğin temel taşlarındandır ve özellikle kümeler konusunun geniş bir uygulama alanıdır. Aralıklar üzerinde yapılan işlemler, kümeler arasındaki ilişkileri anlamamızı sağlar ve sayılarla çalışırken daha esnek bir bakış açısı sunar. Bu nedenle, kümeler ve aralık işlemleri hem matematiksel problemlerde hem de günlük hayatta büyük önem taşır. 9. sınıf düzeyinde bu kavramların iyi anlaşılması, matematiksel düşüncenin gelişmesi için temel oluşturur.