a ve b reel sayı (a ≠ 0) olmak üzere ax + b = 0 biçimindeki denklemlere birinci dereceden bir bilinmeyenli denklemler denir. Bu eşitliği sağlayan x reel sayısına denklemin kökü, köklere denklemin çözümü denir.
DENKLEM ÇÖZÜMÜNDE UYGULANACAK KURALLAR
1. Bir denklemin her iki tarafına aynı sayı eklenir veya çıkarılırsa eşitlik değişmez.
2. Bir denklemin her iki tarafını sıfırdan farklı bir sayı ile böler veya çarparsak eşitlik değişmez.
3. Denklemin çözümü yapılırken bilinenler eşitliğin bir tarafına, bilinmeyenler ise eşitliğin diğer tarafına yazılır.
4. Denklemin bir tarafından diğer tarafına terimlerin işaretleri değiştirilerek geçirilir.
5. Rasyonel ifadeli denklemlerin çözümünde de yukarıdakilerin hepsi yapılabilir ve eşitliğin her iki tarafında paydalar paydaların en küçük ortak katı (EKOK) ile eşitlenip bu paydalardan kurtulunabilir.
Önemli Bilgi: İçinde rasyonel ifadeler bulunan tek değişkenli denklemler rasyonel denklemler olarak isimlendirilir.
Önemli Bilgi: Rasyonel denklemin paydasında bilinmeyen varsa denklemin çözümünde bulunan değerin çözüm olup olmadığına bakılmalıdır. Eğer bulunan değer paydayı sıfır yapıyorsa bu değer denklemin bir çözümü değildir.
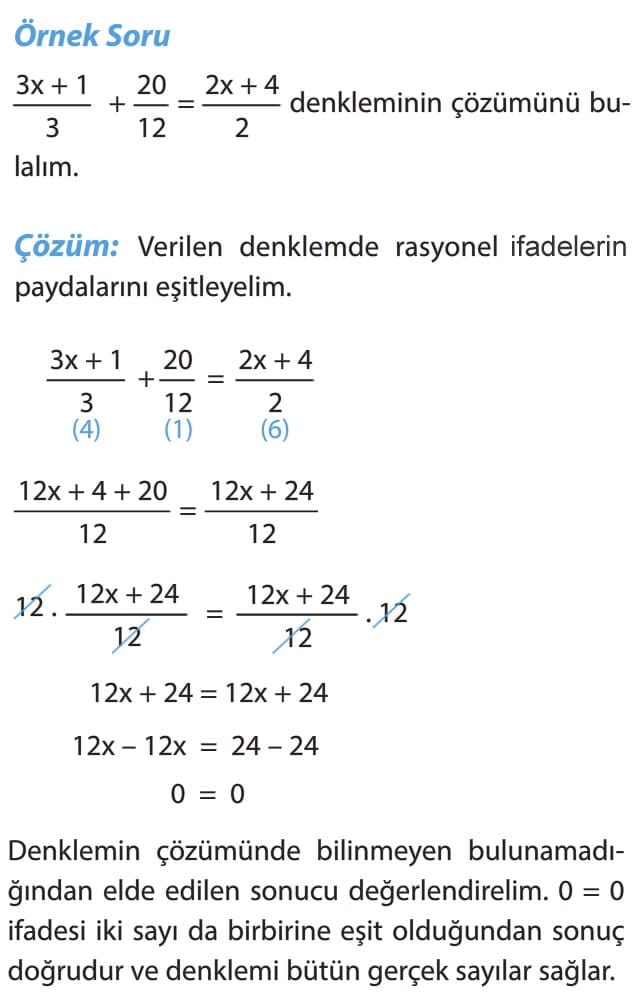
Önemli Bilgi: Herhangi bir denklemin çözümünde bilinmeyenin değeri bulunamıyorsa elde edilen sonuç değerlendirilir. Sonuçta her iki sayı birbirine eşit ise denklemi bütün gerçek sayılar sağlar. Eğer sonuçta sayılar farklı ise eşitlik yanlıştır. Denklemi sağlayan hiçbir gerçek sayı yoktur.
Hatırlayalım: Rasyonel denklem çözümlerinde kesir çizgisi önündeki (-) işaret paya çarpım olarak dağıtılmalıdır.
suna
çok teşekkürler çok iyi anladım