İki veya daha çok olayın birlikte veya birbiri ardına meydana gelmesine bileşik olay denir.
Örneğin, bir zar arka arkaya iki defa atıldığında her iki atışta da 5 gelmesi bir bileşik olaydır.
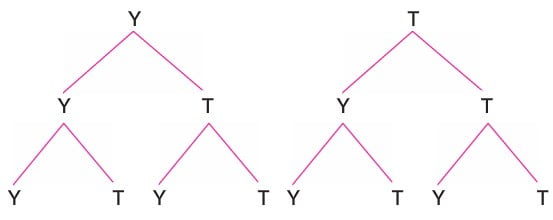
Örneğin, bir paranın arka arkaya 3 defa atılmasının tüm olası durumları aşağıdaki ağaç diyagramında gösterilmiştir.
Bu deneyin örneklem uzayı
E= {YYY, YYT, YTY, YTT, TYY, TYT, TTY, TTT’}
Bu atışlarda 2 defa tura gelmesi olayı bir bileşik olayı olup bu olay A kümesiyle gösterilirse
A = {YTT, TYT, TTY} mümkün sonuçlar olacaktır.
Örneğin, zar atma deneyinde
A = {Tek sayı gelmesi 0Iayı} = {1, 3, 5}
B = {4 den küçük bir sayı gelmesi olayı} = {1, 2, 3}
A ve B olayları tek başlarına değerlendirildiğinde basit olaylar olup birlikte değerlendirilirse birleşik olaylardır.
A u B : Zarın tek sayı veya 4 den küçük bir sayı gelmesi olayı olup, bu bileşik olayın çıktıları
A u B = {1, 2, 3, 5} olacaktır.
A n B : Zarın tek ve 4 ten küçük sayı gelmesi olayı olup bu birleşik olayın çıktıları ise
A n B = {1, 3} olacaktır.
