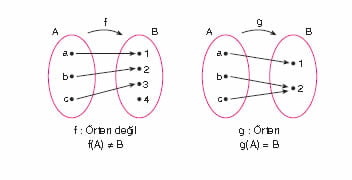
Örten fonksiyon nedir?
f : A → B fonksiyonu için f(A) = B ise yani görüntü kümesi değer kümesine eşit ise f fonksiyonu örten fonksiyondur.
Değer kümesinin her y elemanı için x eksenine paralel çizilen tüm doğrular fonksiyonun grafiğini en az bir noktada kesiyorsa bu fonksiyon örtendir.
ÇÖZÜMLÜ TEST SORULARI
Soru 1:
Aşağıdaki fonksiyonlardan hangisi f: R → R için örten değildir?
A) f(x) = x³
B) f(x) = 2x + 1
C) f(x) = sinx
D) f(x) = x⁵ – x
E) f(x) = eˣ
Çözüm:
E seçeneği (f(x) = eˣ) örten değildir çünkü görüntü kümesi R⁺’dur (pozitif reel sayılar), tüm reel sayıları kapsamaz. Diğer fonksiyonlar tüm reel sayıları kapsar.
Cevap: E) f(x) = eˣ
Soru 2:
f: A → B fonksiyonu için A = {1,2,3,4} ve B = {a,b,c} olmak üzere, hangi fonksiyon örtendir?
A) f(1)=a, f(2)=a, f(3)=b, f(4)=b
B) f(1)=a, f(2)=b, f(3)=c, f(4)=c
C) f(1)=a, f(2)=b, f(3)=b, f(4)=c
D) f(1)=a, f(2)=a, f(3)=a, f(4)=a
E) f(1)=c, f(2)=c, f(3)=c, f(4)=c
Çözüm:
Örten fonksiyon için B kümesinin tüm elemanları görüntü kümesinde olmalıdır. C seçeneğinde a, b ve c değerleri fonksiyon tarafından alınmıştır.
Cevap: C) f(1)=a, f(2)=b, f(3)=b, f(4)=c
Soru 3:
f: R → [0,∞) fonksiyonu f(x) = x² olarak tanımlanıyor. Bu fonksiyon için ne söylenebilir?
A) Birebir ve örten
B) Birebir ama örten değil
C) Örten ama birebir değil
D) Ne birebir ne de örten
E) Sabit fonksiyon
Çözüm:
f(x) = x² fonksiyonu [0,∞) için örtendir çünkü tüm negatif olmayan reel sayıları alır. Ancak birebir değildir (örneğin f(2)=f(-2)=4).
Cevap: C) Örten ama birebir değil
Soru 4:
f: Z → Z fonksiyonu f(x) = 2x + 3 olarak tanımlanıyor. Bu fonksiyon için ne söylenebilir?
A) Örtendir
B) Örten değildir
C) Sabit fonksiyondur
D) Birebir değildir
E) Hem birebir hem örtendir
Çözüm:
f(x) = 2x + 3 fonksiyonu tam sayılarda birebirdir ancak örten değildir çünkü çift sayıları alamaz (örneğin 0 değerini alamaz).
Cevap: B) Örten değildir
Soru 5:
Aşağıdaki fonksiyonlardan hangisi f: R → R için örtendir?
A) f(x) = x² + 1
B) f(x) = |x|
C) f(x) = x³ + 2x
D) f(x) = sinx + 2
E) f(x) = 1/(x²+1)
Çözüm:
C seçeneği (f(x) = x³ + 2x) örtendir çünkü tüm reel sayıları kapsar (kübik fonksiyonlar örtendir). Diğerleri ya belirli bir aralıkta değer alır ya da tüm reel sayıları kapsamaz.
Cevap: C) f(x) = x³ + 2x
Soru 6:
f: A → B fonksiyonu örten ise aşağıdakilerden hangisi kesinlikle doğrudur?
A) A kümesi B kümesinden büyüktür
B) B kümesi A kümesinden büyüktür
C) A ve B kümeleri eşit eleman sayısına sahiptir
D) B kümesinin her elemanı A kümesinde en az bir elemanın görüntüsüdür
E) A kümesinin her elemanı B kümesinde bir elemana eşlenir
Çözüm:
Örten fonksiyon tanımı gereği, B kümesinin her elemanı A kümesinde en az bir elemanın görüntüsü olmalıdır.
Cevap: D) B kümesinin her elemanı A kümesinde en az bir elemanın görüntüsüdür
Soru 7:
f: [-1,1] → [0,1] fonksiyonu f(x) = x² olarak tanımlanıyor. Bu fonksiyon için ne söylenebilir?
A) Birebir ve örten
B) Birebir ama örten değil
C) Örten ama birebir değil
D) Ne birebir ne de örten
E) Sabit fonksiyon
Çözüm:
Verilen aralıkta f(x) = x² fonksiyonu örtendir çünkü [0,1] aralığının tüm değerlerini alır. Ancak birebir değildir (örneğin f(0.5)=f(-0.5)=0.25).
Cevap: C) Örten ama birebir değil