Koordinat Sisteminde Dönme
Dönme Merkezi: Dönme hareketi hangi nokta etrafında oluyorsa bu noktaya dönme merkezi denir. Orijin etrafında dönme hareketinde koordinatlar arasındaki ilişkinin cebirsel ifadesi;
- Köşe noktalarının koordinatları (x, y) olan bir çokgen orijin etrafında ve saat yönünde 90° (saatin tersi yönde 270°) döndürülürse köşe noktalarının yeni koordinatları (y, -x) olur.
- Köşe noktalarının koordinatları (x, y) olan bir çokgen orijin etrafında ve saat yönünde 130” (saatin tersi yönde 180°) döndürülürse köşe noktalarının yeni koordinatları (-x, -y) olur.
- Köşe noktalarının koordinatları (x, y) olan bir çokgen orijin etrafında ve saat yönünde 270° (saatin tersi yönde 90°) döndürülürse köşe noktalarının yeni koordinatları (-y, x) olur.
- 360° döndürüldüğünde şeklin kendisi elde edileceğinden (x, y) koordinatı değişmez.
- 180° lik ve 360° lik döndürmelerde yön belirtilmesine gerek yok.
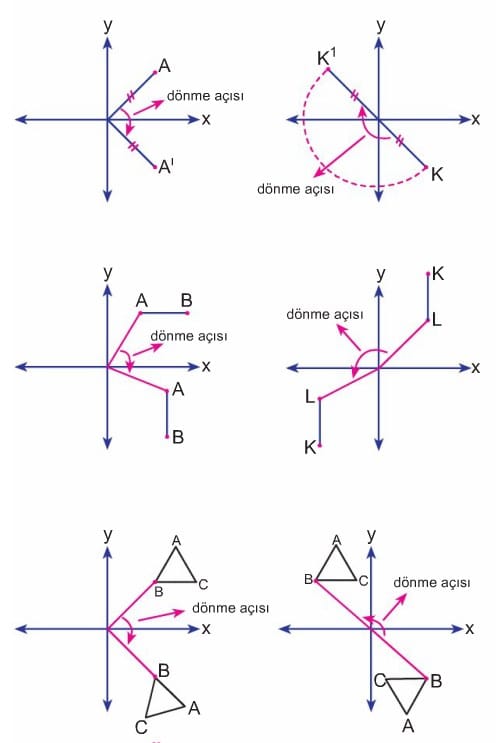
Dönme Açısı
Dönme merkeziyle yapılan açıya dönme açısı denir.
BİR YORUM YAZIN
ZİYARETÇİ YORUMLARI - 0 YORUM
Koordinat Sisteminde Dönme 8.sınıf matematik konu anlatımı
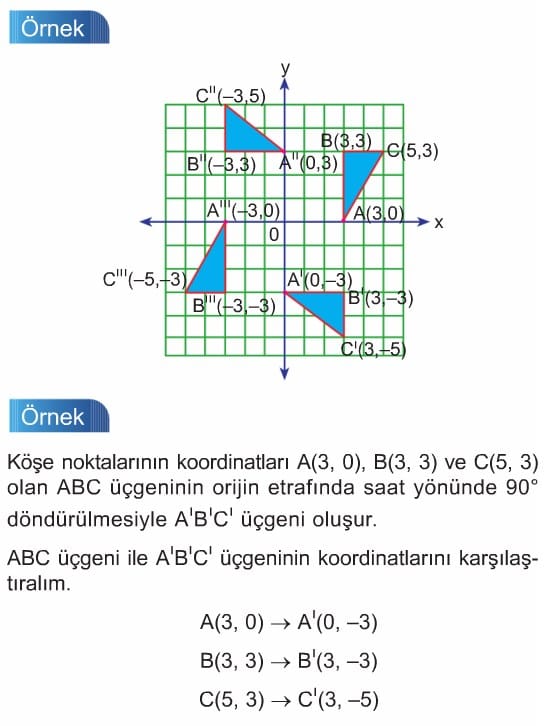
Orijin etrafında saat yönünün tersine 90° döndürdüğümüzde A"B"C" üçgeni oluşur. ABC üçgeni ile A"B"C" üçgeninin koordinatlarını karşılaştıralım.
A(3, O) --> A"(0, 3)
B(3, 3) --> B"(-3, 3)
C(5, 3) --> C"(-3, 5)
Orijin etrafında 180” döndürüldüğünde (her iki yön için)
A''' B''' C''' üçgeni oluşur.
ABC üçgeni ile A''' B''' C''' üçgeninin koordinatlarını karşılaştıralım.
A(3, 0) --> A"'(-3, 0)
B(3, 3) --> B"'(-3, -3)
C(5, 3) --> C"'(-5, -3)