Gerçek Sayıların Üslü Gösterimi (Üslü Sayılar) 9. Sınıf Matematik (Yeni Müfredat)
Üslü ifadeler, bir sayının kendisiyle defalarca çarpılmasını pratik bir şekilde ifade eder. Üs kavramı, matematikte çok kullanılan ve sayıların daha kolay işlem görmesini sağlayan temel bir araçtır. Üslü ifadeler özellikle cebirsel işlemler, denklemler, türev ve integral hesaplarında önemli bir yer tutar. Üslü sayıların kuralları, farklı sayı kümeleri üzerinde de geçerli olup negatif, sıfır ve rasyonel üslerle de genişletilmiştir.
9. Sınıf Gerçek Sayıların Üslü ve Köklü Gösterimleri ile Yapılan İşlemler (Üslü ve Köklü Sayılar) Konuları (Yeni Müfredat)
- 9. Sınıf Gerçek Sayıların Üslü Gösterimi (Üslü Sayılar)
- 9. Sınıf Gerçek Sayıların Üslü Gösterimleriyle Yapılan Toplama, Çıkarma, Çarpma ve Bölme İşlemleri
- 9. Sınıf Üslü Gösterimleri Verilen Sayıların Üssünü Alma İşlemi
- 9. Sınıf Gerçek Sayıların Köklü Gösterimi ile Yapılan İşlemler (Köklü Sayılar)
Konuyu bitirdikten sonra konu ile alakalı test soruları çözebilirsiniz.
9. Sınıf Gerçek Sayıların Üslü Gösterimi Testleri (Yeni Müfredat)
9. Sınıf Gerçek Sayıların Köklü Gösterimi Testleri (Yeni Müfredat)
9. Sınıf Gerçek Sayıların Üslü Gösterimi (Üslü İfadeler) Ders Notu
Üslü İfadenin Tanımı: n pozitif tam sayı ve a gerçek sayı olmak üzere, a sayısının kendisiyle n defa çarpılmasına a nın n. kuvveti denir ve an biçiminde yazılır.
an ifadesine üslü sayı, a ya taban, n ye de üs veya kuvvet denir.
- a > 0 olmak üzere, a0 = 1‘dir.
00 tanımsızdır.
Örneğin;
(-4)0 = 1,
(2013)0 = 1,
(√3)0 = 1 - a sıfırdan farklı gerçek sayı ve n pozitif gerçek sayı olmak üzere

Soru: Aşağıda verilen sayıları hesaplayın.
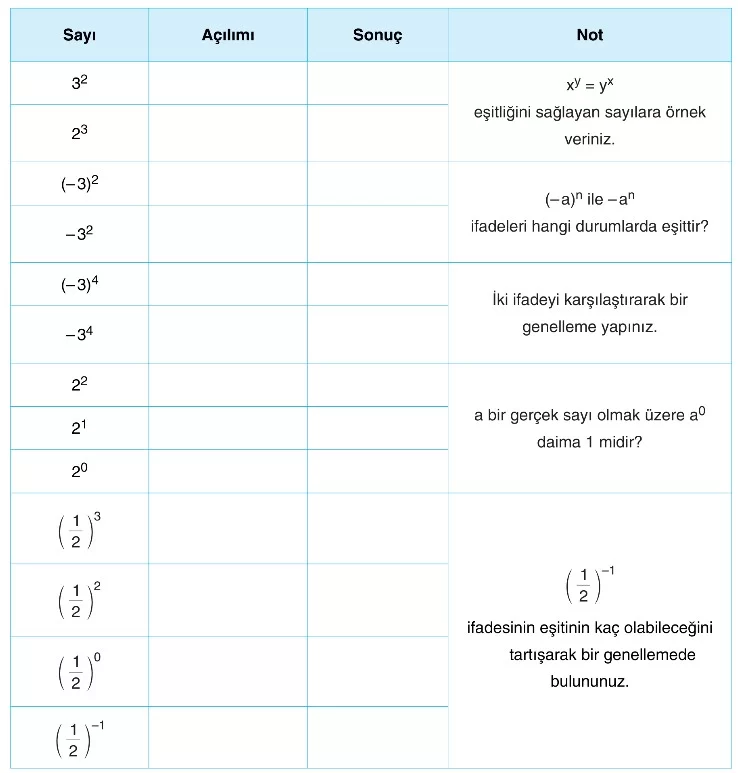

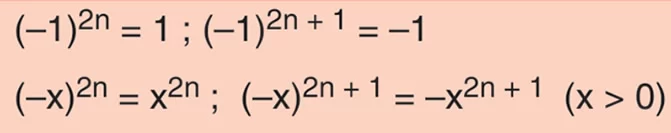
“Negatif bir sayının çift sayı kuvvetlerinin sonucu pozitif, tek sayı kuvvetlerinin sonucu negatiftir.”
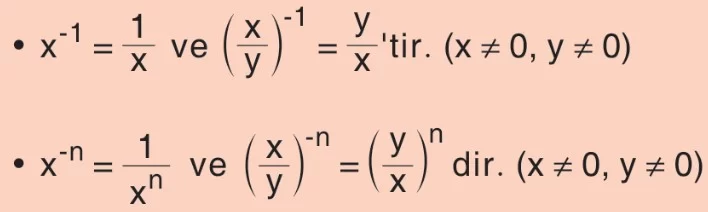
Örnek:

Bilimsel Gösterim
- |a|, 1 veya 1’den büyük, 10’dan küçük bir gerçek sayı ve n bir tam sayı olmak üzere a.10ⁿ gösterimine bilimsel gösterim denir.
1 ≤ |a| < 10 - Çok büyük ve çok küçük sayıları 10’un tam sayı kuvvetleri yardımıyla yazmak kolaylık sağlar.
- Dünya’nın içinde bulunduğu Samanyolu galaksisi kendi etrafındaki bir turunu 230 000 000 yılda tamamlamaktadır.
Bu süreyi bilimsel olarak gösterelim.
230 000 000 = 23·10⁷ yıl
23 sayısını 1 ile 10 arasında ifade edersek:
23·10⁷ = 2,3·10⁸ yıl olur.
Gerçek Sayıların Üslü Gösterimi Çözümlü Sorular
Çözümlü Örnek Test Soruları
Soru 1
2³ × 2⁴ işleminin sonucu kaçtır?
A) 2⁶
B) 2⁷
C) 2⁸
D) 2¹²
E) 4³
Çözüm
Aynı tabanlı iki üslü sayı çarpılırken üsler toplanır:
2³ × 2⁴ = 2⁷
Cevap: B
Soru 2
3⁵ ÷ 3² işleminin sonucu kaçtır?
A) 3²
B) 3³
C) 3⁵
D) 3⁷
E) 3¹⁰
Çözüm
Aynı tabanlı iki üslü sayı bölünürken üsler çıkarılır:
3⁵ ÷ 3² = 3³
Cevap: B
Soru 3
(5²)³ işleminin sonucu kaçtır?
A) 5⁵
B) 5⁶
C) 5⁸
D) 5¹⁰
E) 5¹²
Çözüm
Bir üslü sayının üssü alınırken, üsler çarpılır:
(5²)³ = 5⁶
Cevap: B
Soru 4
2⁴ × 3⁴ işlemi aşağıdakilerden hangisine eşittir?
A) 6⁴
B) 5⁴
C) 4⁴
D) 3⁸
E) 2⁸
Çözüm
Aynı üsse sahip çarpanların çarpımı, tabanların çarpımı üssün altında toplanarak yazılabilir:
2⁴ × 3⁴ = 6⁴
Cevap: A
Soru 5
10⁻² ifadesinin değeri aşağıdakilerden hangisidir?
A) 100
B) 10
C) 1
D) 0.1
E) 0.01
Çözüm
Negatif üs, sayının tersini ifade eder:
10⁻² = 1 ÷ 10² = 0.01
Cevap: E
Soru 6
4⁻¹ × 2² işleminin sonucu kaçtır?
A) 2
B) 4
C) 8
D) 16
E) 0.5
Çözüm
4⁻¹ = 1 ÷ 4 = 0.25 ve 2² = 4 olduğuna göre:
4⁻¹ × 2² = 1
Cevap: C
Soru 7
9¹ᐟ² işleminin sonucu kaçtır?
A) 1
B) 2
C) 3
D) 4
E) 9
Çözüm
Üs 1/2 olduğunda karekök işlemi anlamına gelir:
9¹ᐟ² = 3
Cevap: C
Soru 8
2³ ÷ 4¹ᐟ² işleminin sonucu kaçtır?
A) 2
B) 4
C) 6
D) 8
E) 16
Çözüm
4¹ᐟ² = 2 olduğundan işlem şu şekilde yapılır:
2³ ÷ 2 = 4
Cevap: B
Üslü İfadelerin Uygulamaları: Üslü ifadeler, günlük yaşamda ve bilimsel hesaplamalarda oldukça yaygındır. Örneğin:
- Büyüklük hesaplamalarında (mesafeler, hızlar vs.),
- Bilgisayarlarda veri boyutlarının gösteriminde (kilobyte, megabyte, gigabyte),
- Bileşik faiz hesaplamalarında,
- Atom seviyesindeki çok küçük veya çok büyük sayıların gösteriminde kullanılır.
Üslü ifadeler, matematiksel işlemlerde önemli bir yer tutar ve birçok alanda kullanılır. Üslerin temel kurallarını anlamak, daha karmaşık matematiksel işlemleri kolaylaştırır. Üslü ifadeler hem teorik matematikte hem de pratik hesaplamalarda kritik bir rol oynar ve doğru kullanımını öğrenmek matematiksel yetkinlik açısından önemlidir.







Allah razı olsun diyorum başka da bir şey demiyorum. Onuncu sınıfım ve okullar açıldığı anda matematikçinin 9. sınıf konularından yapacağı sınav duyurusuyla telaşa kapılmıştım ama bu siteden konuları tekrar hatırladım. Kısa ve öz, gereksiz bilgiler yok. Çok iyi bir kaynak.
efsane
Üslü ifadeler konusu ancak bu kadar güzel anlatılabilirdi. Konuyla ilgili her türlü içerik eklenmiş. Üslü sayılar hem ders notları hem de üslü sayılarla ilgili konu anlatımı ve soru çözümü videoları bulunuyor. Hazırlayanın emeğine sağlık, teşekkür ederiz…
Muhteşem olmuş 20dkda tüm konuyu anladim