Vektörlerin Toplanması konusu, fiziksel büyüklüklerin yön ve büyüklüğe göre nasıl birleştirileceğini öğretir. 9. sınıf fizik müfredatında bu konu, iki ya da daha fazla vektörün nasıl toplandığını açıklayan temel bir kavramdır.

Nicelikleri toplarken ilk kural, toplanacak vektörlerin birbirleriyle aynı niceliğe ve aynı birime sahip olması gerektiğidir. Örneğin, hız ve kuvvet vektörlerini toplamak doğru olmaz. Çünkü kuvvet ve hız farklı fiziksel büyüklüklerdir. 30 m/s hız ile 60 km/h hız toplanamaz. Aynı nicelikte olmalarına rağmen, farklı birimlere sahiptirler. Hızların birimlerinin aynı olması halinde ise vektörel toplama yapılabilir.

Skaler ifadeler toplanırken cebirsel işlemler yapılabilir. Örneğin, 2 kg elma ile 3 kg elma toplandığında 5 kg elma elde edilir. Fakat vektörel ifadelerde, vektörlerin yönleri dikkate alınarak toplama yapılmalıdır. Örneğin, 30 N’luk kuvvet ile 20 N’luk kuvvet her zaman 50 N yapmaz. Sadece aynı yönlü olduklarında bu değer 50 N olur. Örneğin, kürek takımındaki sporcuların aynı yönde kuvvet uygulamalarıyla büyük bir bileşke kuvvet oluşur.

Bu bölümde vektörlerin toplanma yöntemlerini inceleyeceğiz: Uca ekleme yöntemi, paralelkenar yöntemi ve dik bileşenlere ayırma yöntemleri gibi teknikleri öğrenmiş olacağız.

Birden fazla vektörün oluşturduğu etkiyi tek başına ifade eden vektöre bileşke ya da toplam vektör denir. Bileşke vektör, uç uca ekleme yöntemi, dik bileşenlerine ayırma ve paralelkenar yöntemi ile bulunabilir.

Uç Uca Ekleme Yöntemi

Vektörlerin doğrultusu, yönü ve büyüklüğü değiştirilmeksizin, bir vektörün bitiş noktası, diğer vektörün başlangıç noktasına gelecek şekilde vektörler uç uca eklenir. İlk vektörün başlangıç noktasından, son vektörün bitiş noktasına çizilen vektör, bileşke vektörü olarak adlandırılır. Bileşke vektör genellikle R harfiyle gösterilir.

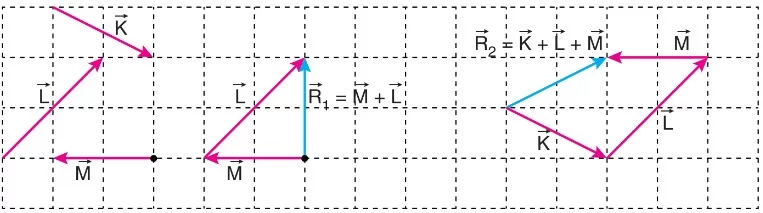
Birim karelere bölünmüş düzlemde K, L, M vektörleri ile R1 = M + L ve R2 = K + L + M vektörleri uç uca ekleme yöntemiyle bulunmuştur. Bu yöntemde vektörler her zaman uç uca eklenme sırasına göre toplanır.

---

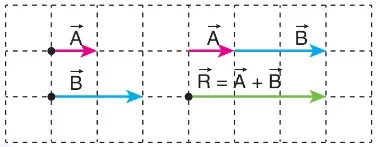
Aynı Doğrultuda Yer Alan Vektörlerin Uç Uca Ekleme Yöntemiyle Toplanması

Şekildeki A vektörü ile B vektörü aynı yöndedir. Vektörlerin bileşkeleri de aynı yönde olur. Bileşke vektörün büyüklüğü, vektörlerin büyüklüklerinin toplamına eşittir.

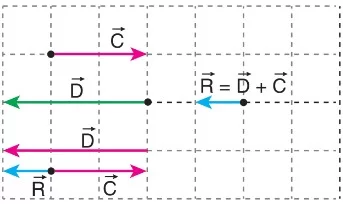
Şekildeki C ve D vektörleri zıt yönlüdür.
Vektörlerin bileşkesinin yönü, büyük vektör yönünde olur. Bileşke vektörün büyüklüğü, vektörlerin büyüklüklerinin farkına eşittir.

Farklı Doğrultudaki Vektörlerin Uç Uca Ekleme Yöntemiyle Toplanması

Farklı doğrultudaki vektörler uç uca ekleme yöntemiyle toplanırken bazı vektörler doğrultuları ve yönleri değiştirilmeden taşınarak bileşke bulunur. Bu yöntemde bir vektörün okuna diğer vektörün başlangıç noktası eklenmelidir. (Toplanacak vektörlerin başlangıç noktaları ya da okları çakışmamalıdır.) Hepsi bu şekilde eklendikten sonra ilk vektörün başlangıç noktasından son vektörün okuna çizilen vektör bileşke vektördür.

Uç uca eklenen vektörler kapalı bir bölge oluşturuyorsa bu vektörlerin bileşkesi sıfırdır.
K + L + N + M = 0

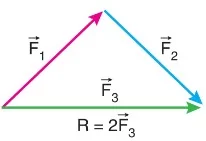
Her kapalı vektör sisteminin bileşkesi sıfır olmayabilir. Uç uca eklenip eklenilmediğine bakılmalıdır. Şekildeki gibi eklenen F1, F2, F3 vektörlerinin bileşkesi sıfır değildir.

Vektörlerde Çıkarma İşlemi

İki vektörün çıkarılması da aslında bir vektörel toplama işlemidir. Çıkarılacak vektörün yönü ters çevrilip diğer vektör ile toplanır. F1 – F2 bulunurken, F2 vektörünün yönü ters çevrilip F1 vektörü ile toplanır.

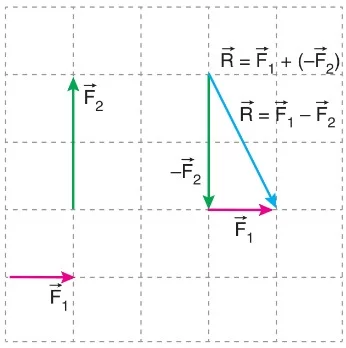
Örneğin, şekildeki F1 ve F2 vektörleri arasında F1 – F2 işlemi yapılırken, F2 vektörü ters çevrilir. F1 vektörünün başlangıç noktası, ters çevrilmiş F2 vektörünün okuna eklenir. En son -F2 kuvvetinin başlangıç noktasından F1 vektörünün okuna çizilen vektör, F1 – F2 vektörüdür.

F1 – F2 = F1 + (-F2)

Özet:

1. Uç Uca Ekleme Yöntemi

Bu yöntemle vektörler uç uca eklenerek toplanır. İlk vektörün bitiş noktasına ikinci vektörün başlangıcı eklenir. İki vektörün toplamı, ilk vektörün başlangıcından son vektörün bitişine kadar olan çizgidir. Bu çizgi, toplam (bileşke) vektörü gösterir.

Örnek: A ve B vektörleri uç uca eklenir. A’nın bitiş noktası ile B’nin başlangıç noktası birleştirilir ve toplam vektör bulunur.

2. Paralelkenar Yöntemi

Bu yöntem, iki vektörün başlangıç noktalarının aynı olduğu durumda uygulanır. İki vektörden bir paralelkenar oluşturulur. Paralelkenarın köşegenlerinden biri, iki vektörün toplamını (bileşke) verir.

Örnek: A ve B vektörleri başlangıç noktalarından çizilir. Bu iki vektörle paralelkenar çizilir ve köşegeni, toplam vektörü gösterir.

3. Bileşenlerine Ayırma Yöntemi

Vektörler, x ve y eksenine paralel bileşenlerine ayrılarak toplanabilir. Bu yöntem, özellikle farklı yönlerde olan vektörler için kullanışlıdır. X eksenindeki bileşenler kendi aralarında, y eksenindeki bileşenler de kendi aralarında toplanır.

Örnek: Vektörler yatay ve dikey bileşenlere ayrılır, ardından her eksendeki toplam vektör bulunur.

Sonuç

Vektörlerin toplanması, yön ve büyüklüğün dikkatli bir şekilde ele alınmasını gerektirir. Doğru yöntemle vektörleri birleştirerek fiziksel büyüklüklerin bileşkesini bulmak, birçok fiziksel problemi çözmekte kullanılır.