Testlerin altında Üçgenlerde Eşlik Çözümlü Sorular yer almaktadır. Testleri çözmeye başlamadan önce çözümlü sorulara bakmanızı tavsiye ederiz. Çözümlü sorular Üçgenlerde Eşlik konusunu özetlemektedir.

Üçgenlerde Eşlik Test 1 Çöz

Üçgenlerde Eşlik Çözümlü Sorular

Herhangi iki ABC ve DEF üçgenleri için
|AB| = |DE|
|AC| = |DF|
|BC| = |EF| ve
m(A) = m(D)
m(B) = m(E)
m(C) = m(F)
koşulları sağlıyorsa bu iki üçgene eş üçgenler denir ve ABC eştir DEF biçiminde ifade edilir. ABC eştir DEF üçgeni ise
– Karşılıklı tüm açıların ölçüleri eşittir.
– Karşılıklı tüm kenarların uzunlukları eşittir.
– Üçgenlerin çevreleri eşittir.
– Üçgenlerin alanları eşittir.

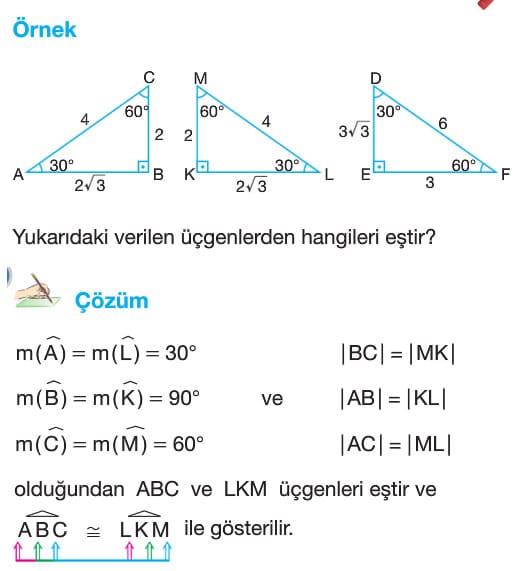
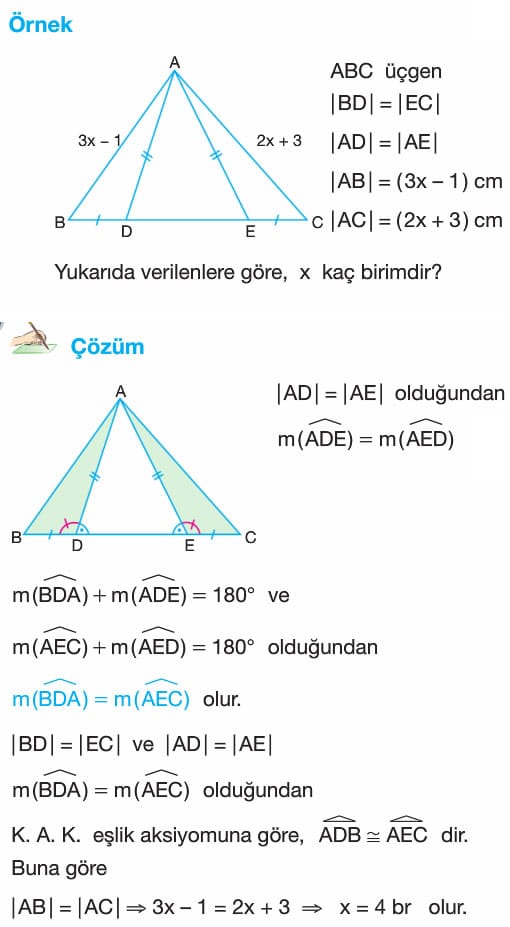
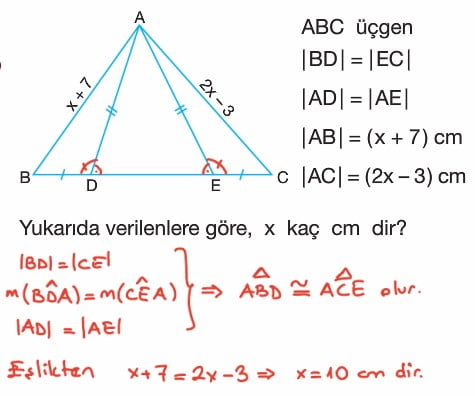
Örnek: ABC bir üçgen
|BD|=|EC|, |AD|=|AE|
|AB| = (3x-1)cm, |AC| = (2x + 3) cm
Yukarıda verilenlere göre, x kaç birimdir?

Kenar Açı Kenar Eşliği: Herhangi iki üçgenin ardışık iki kenar uzunluğu ve bu kenarlar arasında kalan açıların ölçüleri birbirine eşit ise bu üçgenler birbirine eştir denir.
|AB|= |DE|, |BC| = |EF|  ve m (ABC) = m(DEF) ise ABC ve DEF üçgenleri eştir ve ABC eştir DEF biçiminde ifade edilir. Üçgenlerin eşliğinin bu şekilde odaya konulmasına Kenar Açı Kenar (K. A. K.) eşlik teoremi denir.

Çözüm: |AD| = |AE| olduğundan m (ADE) = m(AED)
m(BDA) + m (ADE) = 180° ve m(AEC) + m(AED) = 180° olduğundan
m(BDA) = m(AEC) olur.
|BD| = |EC| ve |AD| = |AE|
m(BDA) = m(AEC) olduğundan
K. A. K. eşlik aksiyomuna göre, ADB eştir AEC dir. Buna göre
|AB| = |AC| ise 3x – 1 = 2x + 3 ise x = 4 br olur.

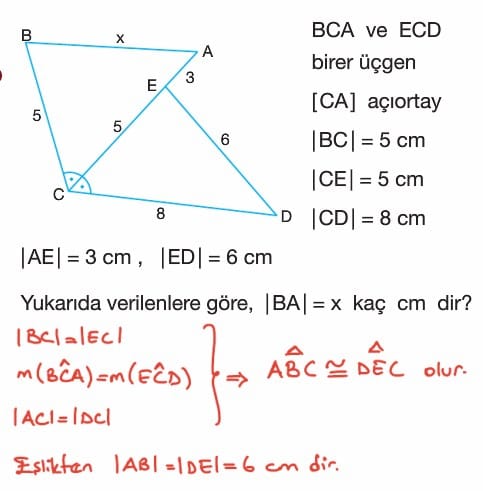
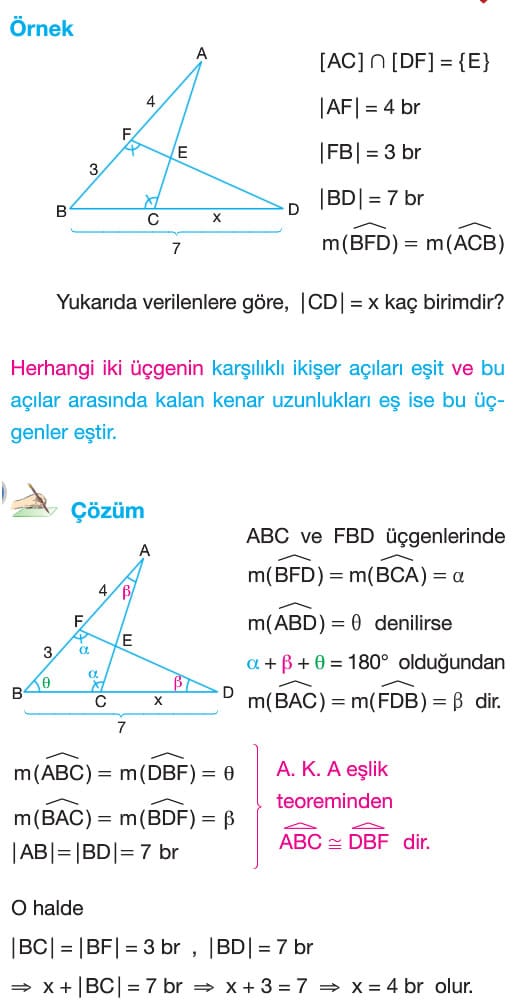
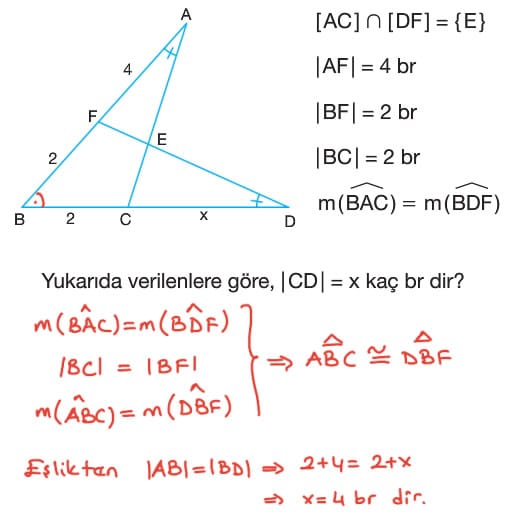
Örnek: [AC] ∩ [DF] = {E}
|AF| = 4 br
|FB| = 3 br
|BD| = 7 br
m(BFD) = m(ACB)
Yukarıda verilenlere göre, |CD| = x kaç birimdir?

Açı Kenar Açı Eşliği: Herhangi iki üçgenin karşılıklı ikişer açılan eşit ve bu açılar arasında kalan kenar uzunlukları eş ise bu üçgenler eştir.
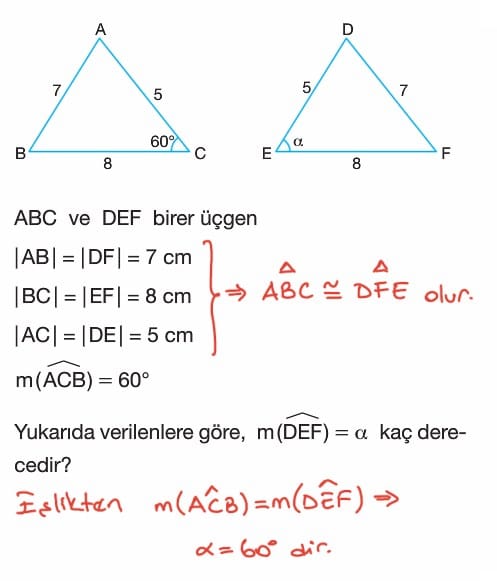
ABC ve DEF üçgenleri için
m(ABC) = m(DEF)
m(ACB)= m(DFE) ve |BC| = |EF| ise ABC ve DEF üçgenleri eştir ve ABC eştir DEF biçiminde ifade edilir. Üçgenlerin bu şekilde eşliğinin ortaya konulmasına Açı Kenar Açı (A. K. A.) eşlik teoremi denir.

Çözüm: ABC ve FBD üçgenlerinde m(BFD) = m(BCA) = alfa
m(ABD) = teta denilirse alfa + beta + teta = 180° olduğundan
m(BAC) = m(FDB) = beta dır.
m(ABC) = m(DBF) = teta
m (BAC) = m (BDF) = beta olduğundan açı kenar açı eşlik teoreminden ABC ve DBF üçgenleri eştir.
|AB|=|BD|= 7 br
O halde
|BC|=|BF|=3br , |BD|=7br
ise x + |BC| = 7 br ise x + 3 = 7 ise  x = 4 br olur.

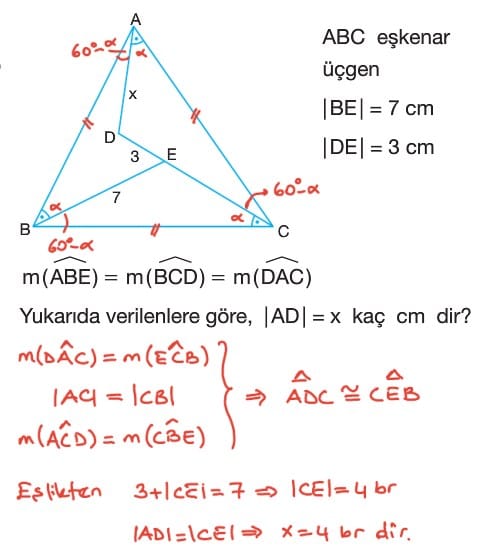
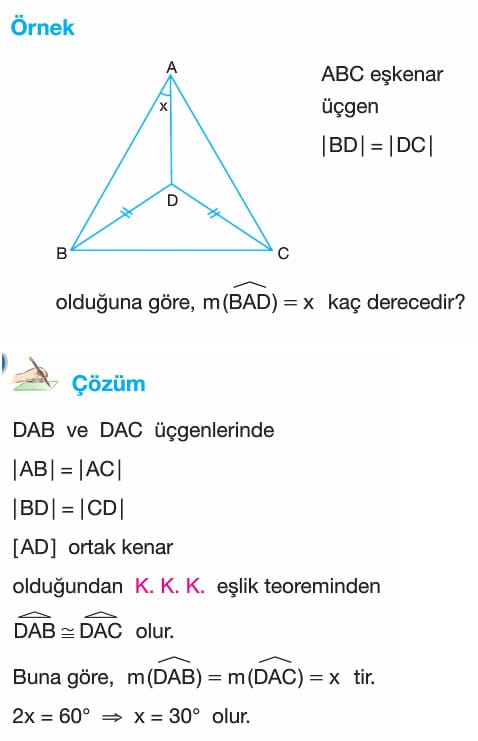
Örnek: ABC eşkenar üçgenve |BD|=|DC| olduğuna göre, m (BAD) = x kaç derecedir?

Kenar Kenar Kenar Eşliği: Herhangi iki üçgenin karşılıklı üç kenar uzunluğu birbirine eşit ise bu üçgenler eştir.
ABC ve DEF üçgenleri için |AB| = |DE|, |BC| = |EF|ve |AC| = |DF|
ise ABC ve DEF üçgenleri eştir ve ABC eştir DEF biçiminde ifade edilir. Üçgenlerin bu şekilde eşliğinin ortaya konulmasına Kenar Kenar Kenar (K. K. K.) eşlik teoremi denir.
Not : Üçgenlerin eşliği için A. A. A. teoremi gerçekleşmez. Üç açısı da aynı olan üçgenler eş olmak zorunda değildir.

Çözüm: DAB ve DAC üçgenlerinde |AB|= |AC|, |BD|=|CD| ve [AD] odak kenar olduğundan K. K. K. eşlik teoreminden DAB eştir DAC olur. Buna göre, m(DAB) = m (DAC) = x tir.
2x = 60° ise x = 30° olur.