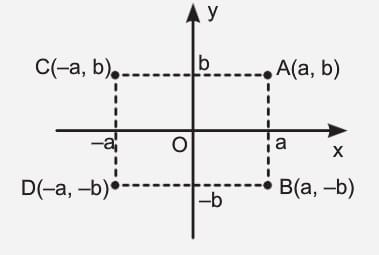
Bir A(a, b) noktasının;

• Ox eksenine göre simetriği B(a, —b) (apsis sabit kalır, ordinat işaret değiştirir).
• Oy eksenine göre simetriği C(—a, b) (ordinat sabit kalır, apsis işaret değiştirir).
• Orijine göre simetriği D(—a, —b) (apsis ve ordinat işaret değiştirir).

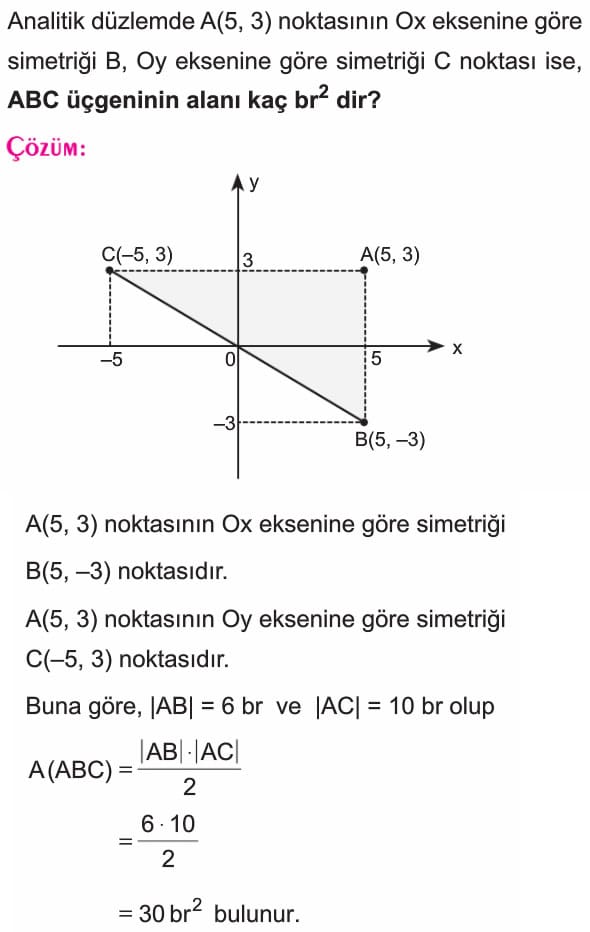
Noktanın Noktaya Göre Simetriği

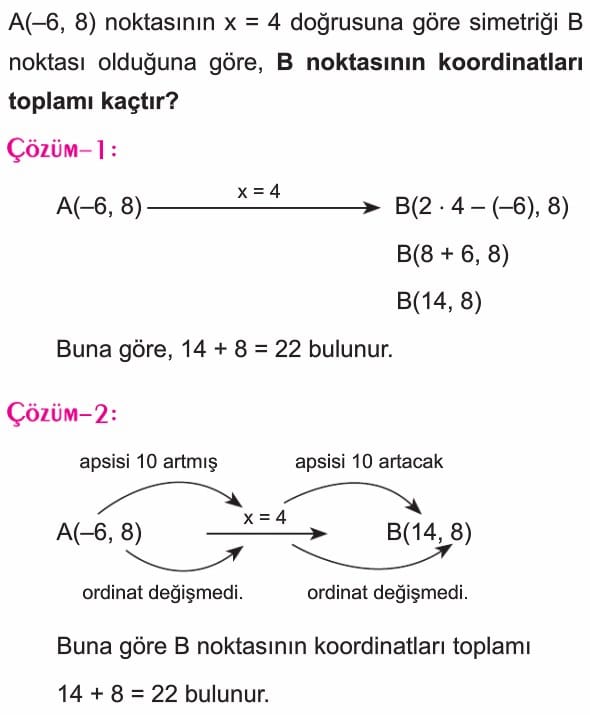
Bir Noktanın x = a Doğrusuna Göre Simetriği

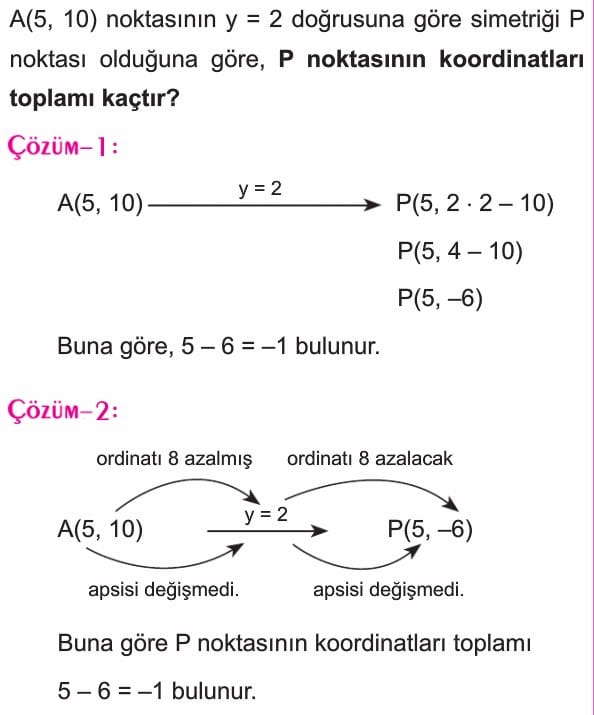
Bir Noktanın y = b Doğrusuna Göre Simetriği

Bir Noktanın y = x (1. Açıortay)  Doğrusuna Göre Simetriği

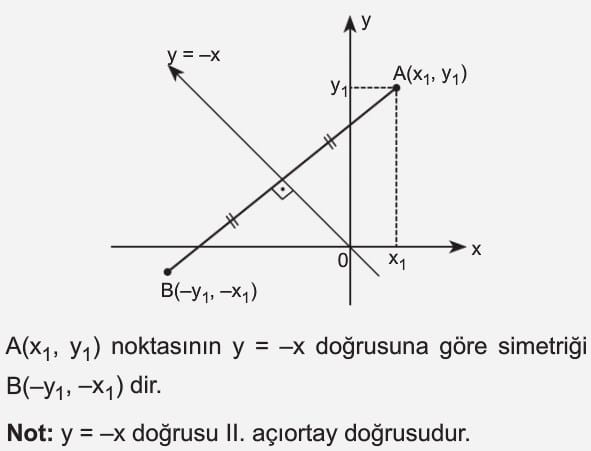
Bir Noktanın y = –x (2. Açıortay)  Doğrusuna Göre Simetriği

Doğrunun Simetriği

ax + by + c = 0 doğrusunun 8 ayrı duruma göre simetri dönüşümü altındaki görüntüleri, noktanın simetriğinde uygulanan yöntemlerle aynıdır.

Örnek:

2x – 3y + 6 = 0 doğrusunun,

1. x eksenine göre simetriği (x, -y)
2x – 3(-y) + 6 = 0 ⇒ 2x + 3y + 6 = 0 dır.

2. y eksenine göre simetriği (-x, y)
2(-x) – 3y + 6 = 0 ⇒ -2x – 3y + 6 = 0 dır.

3. Orijine göre simetriği (-x, -y)
2(-x) – 3(-y) + 6 = 0 ⇒ -2x + 3y + 6 = 0 dır.

4. y = x doğrusuna göre simetriği (y, x)
2y – 3x + 6 = 0 ⇒ -3x + 2y + 6 = 0 dır.

5. y = -x doğrusuna göre simetriği (-y, -x)
2(-y) – 3(-x) + 6 = 0 ⇒ -2y + 3x + 6 = 0 dır.

6. x = 4 doğrusuna göre simetriği (2 • 4 – x, y)
2(8 – x) – 3y + 6 = 0 ⇒ -2x – 3y + 22 = 0 dır.

7. y = -2 doğrusuna göre simetriği (x, 2 • (-2) – y)
2x – 3(-4 – y) + 6 = 0 ⇒ 2x + 3y + 18 = 0 dır.

8. B(2, 1) noktasına göre simetriği (2 • 2 – x, 2 • 1 – y)
2(4 – x) – 3(2 – y) + 6 = 0 ⇒ -2x + 3y + 8 = 0 dır.

Not: Verilen denklem doğru olmayıp, çember, parabol, elips, hiperbol, denklemleri de olsa, yukarıda uygulanan teknikler aynen uygulanabilir.

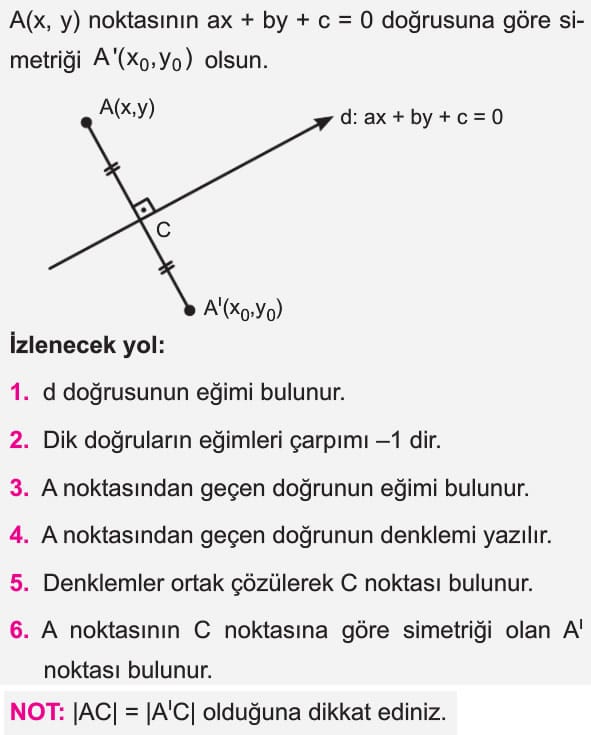
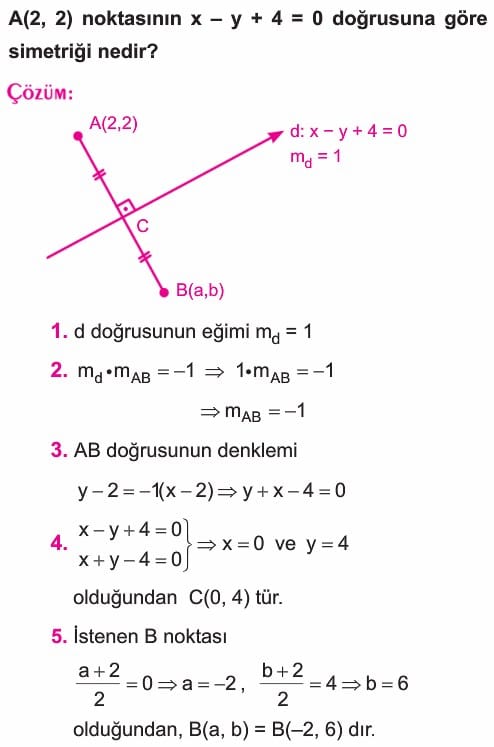
Noktanın Doğruya Göre Simetriği

Doğrunun Noktaya Göre Simetri Dönüşümü

Örnek:

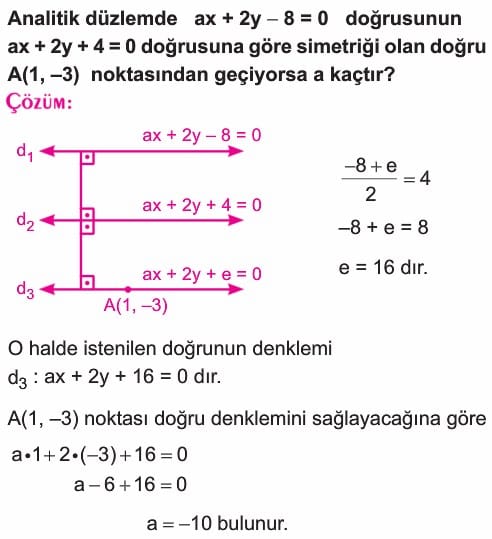
Doğrunun Doğruya Göre Simetriği

1. Doğrular Paralel İse

2. Doğrular Kesişiyor İse

Çözümlü Örnek Test Soruları: Simetri Dönüşümü

1. Noktaların x eksenine göre simetri dönüşümüyle ilgili aşağıdaki ifadelerden hangisi doğrudur?
A) x koordinatı değişir, y koordinatı aynı kalır.
B) x koordinatı aynı kalır, y koordinatının işareti değişir.
C) Hem x hem de y koordinatları değişir.
D) x ve y koordinatları yer değiştirir.

Çözüm:
Bir noktanın x eksenine göre simetriği alınırken x koordinatı sabit kalır, ancak y koordinatının işareti değişir.
Örneğin, (3,4) noktasının x eksenine göre simetriği (3,-4) olur.
Cevap: B

---

2. A(4, -6) noktasının y eksenine göre simetriği aşağıdakilerden hangisidir?
A) (-4, -6)
B) (4, 6)
C) (-4, 6)
D) (4, -6)

Çözüm:
Bir noktanın y eksenine göre simetriği alınırken x koordinatının işareti değişir, ancak y koordinatı sabit kalır.
A(4, -6) noktasının y eksenine göre simetriği (-4, -6) olur.
Cevap: A

---

3. A(3, -5) noktasının orijine göre simetriği aşağıdakilerden hangisidir?
A) (-3, -5)
B) (-3, 5)
C) (3, 5)
D) (-3, -5)

Çözüm:
Bir noktanın orijine göre simetriği alındığında hem x hem de y koordinatlarının işareti değişir.
Örneğin, A(3, -5) noktasının orijine göre simetriği (-3, 5) olur.
Cevap: B

---

4. B(2, -3) noktasının y = x doğrusuna göre simetriği aşağıdakilerden hangisidir?
A) (-3, 2)
B) (3, -2)
C) (-2, -3)
D) (-3, -2)

Çözüm:
Bir noktanın y = x doğrusuna göre simetriği alınırken, x ve y koordinatları yer değiştirir.
Bu durumda B(2, -3) noktasının simetriği (-3, 2) olur.
Cevap: A

---

5. Bir üçgenin y eksenine göre simetrisi alındığında, aşağıdaki ifadelerden hangisi yanlıştır?
A) Üçgenin şekli değişmez.
B) Üçgenin alanı değişmez.
C) Üçgenin x koordinatları işaret değiştirir.
D) Üçgenin y koordinatları işaret değiştirir.

Çözüm:
Bir şeklin y eksenine göre simetriği alındığında, x koordinatlarının işareti değişir, ancak y koordinatları sabit kalır.
Yanlış olan ifade D seçeneğidir, çünkü y koordinatları değişmez.
Cevap: D

Soru: A(-3, 1) noktasının; Ox eksenine göre simetriği B, B noktasının orijine göre simetriği C, C noktasının Oy eksenine göre simetriği D ise, C ve D noktalarından geçen doğrunun eğimi kaçtır?
Çözüm: A(-3, 1) in Ox eksenine göre simetriği B(-3, —1)
B(-3, —1) in orijine göre simetriği C(3, 1)
C(3, 1) in Oy eksenine göre simetriği D(-3, 1) olduğuna göre; m_CD = 0 bulunur.

izlenecek yol:

• d doğrusunun eğimi bulunur.
• Dik doğruların eğimleri çarpımı —1 dir.
• A noktasından geçen doğrunun eğimi bulunur.
• A noktasından geçen doğrunun denklemi yazılır.
• Denklemler odak çözülerek C noktası bulunur.
• A noktasının C noktasına göre simetriği olan A’ noktası bulunur.

PRATİK YOL: A(x1 , y1) noktasının ax + by + c = 0 doğrusuna göre simetriğinde doğrunun eğimi 1 veya —1 ise noktanın apsisi doğrunun denkleminde yazılarak simetri dönüşümü altındaki görüntü noktanın ordinatı bulunur. Noktanın ordinatı doğrunun denkleminde yazılarak simetri dönüşümü altındaki görüntü noktanın apsisi bulunur.

Soru: 4x — 3y — 6 = 0 doğrusunun P(-1, 2) noktasına göre simetriği olan doğrunun denklemi nedir?
d1 : 4x — 3y — 6 = 0 doğrusunun P(-1, 2) noktasına göre simetriği d2 : 4x — 3y + c = 0 doğrusudur. P noktasından geçen d1 ve d2 doğrularına paralel olacak şekilde d3 doğrusunun denklemi 4x — 3y + k = 0 olsun. d3 doğrusu P(-1, 2) den geçtiğine göre doğru denklemini sağlar.
Buna göre, 4 • (-1) — 3(2) + k = O ve k = 10 bulunur. d1 ve d3 ün sabitleri 16 artmış olduğundan d3 ve d2 nin sabitleri de 16 artar. c = 26 olur. Buna göre, d2 : 4x — 3y + 26 = 0 denklemi elde edilir.

Soru: Analitik düzlemde 3x + 5y — 1 = 0 doğrusunun 3x + 5y — 6 = 0 doğrusuna göre simetriği olan doğrunun denklemi nedir?
A) 3x + 5y — 7 = 0 B) 3x + 5y — 10 = 0
C)3x+5y-11= 0            D) 3x + 5y + 12 = 0
E) 3x + 5y — 13= 0

Soru: Analitik düzlemde d1 : ax + 7y — 10 = 0 doğrusunun d2 : 5x + by + 3 = 0 doğrusuna göre simetriği olan doğru d3 : cx + dy — e = 0 doğrusu ise a+b+c+d+e toplamı kaçtır? (d1 // d2 // d3)
A) 3 B) 4 C) 6     D) 7     E) 8

Soru: Analitik düzlemde 5x — by + 4 = 0 doğrusunun 5x — by + 12 = 0 doğrusuna göre simetriği olan doğru A(2, 1) noktasından geçen b kaçtır?
A) 32   B) 30   C) 28   D) 26   E) 24

Soru: 3x + y — 5 = 0 doğrusunun A(1, 1) noktasına göre simetriği olan doğrunun denklemi aşağıdakilerden hangisidir?
A) 3x+y— 1 =0    B) 3x+y= 0    C) 3x+y-4 = 0
D) 3x + y — 3 = 0    E) 3x + y — 2 = 0

Soru: y+x=0 doğrusunun A(-2, 3) noktasına göre simetriği aşağıdakilerden hangisidir?
A) y—x+ 4 = 0 B) y—x+ 2 = 0 C) x+y+ 1= 0
D) x+y-2 = 0    E) x+y+ 2 =0