KÜTLE (AĞIRLIK) MERKEZİ
Uzayda yer kaplayan, eylemsizlik gösteren tüm cisimlerin madde miktarına kütle denir. Skâler büyüklüktür ve birimi kilogram (kg) dır. m ile gösterilir, eşit kollu terazi ile ölçülür.
Bir cisme etki eden yerçekimi kuvvetine ağırlık denir. Vektörel bir büyüklüktür ve yönü daima yerin merkezine doğrudur. Birimi Newton veya dyn’dir. G ile gösterilir. Dinamometre ile ölçülür.
Maddeyi meydana getiren bütün parçacıklara etki eden yerçekimi kuvvetlerinin bileşkesinin uygulama noktasına ağırlık merkezi denir.
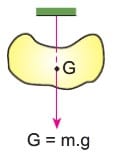
Cismin ağırlık merkezi aynı zamanda kütle merkezidir. Ağırlık merkezinden asılan tüm cisimler dengede kalır ve asıldığı ipin uzantısı ağırlık merkezinden geçer.
Kütle Merkezinin Bulunması
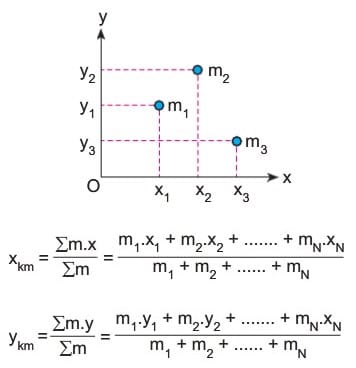
Noktasal cisimlerin ortak kütle merkezi cisimleri birleştiren doğrunun üzerinde büyük olan daha yakındır. Kütle merkezinin yerini bulmak için, paralel kuvvetlerin bileşkesinin uygulama noktası bulunur.
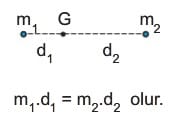
Düzgün, türdeş cisimlerin kütle merkezi
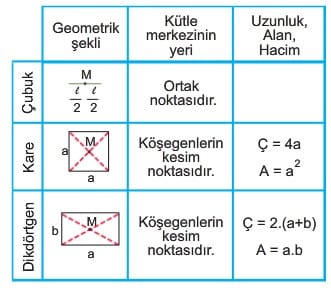
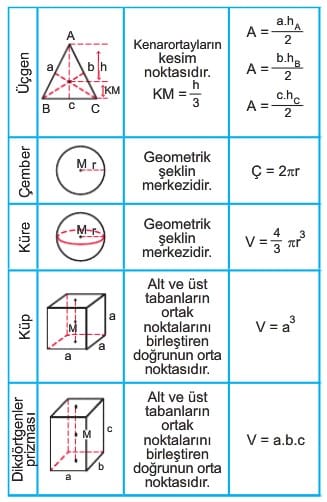
Türdeş olmayan cismin kütle merkezi
Cisim farklı noktalardan asılır, daha sonra düşey doğrultuların kesişme noktası tespit edilir. Bu nokta cismin ağırlık merkezini verir.
Denge Durumları
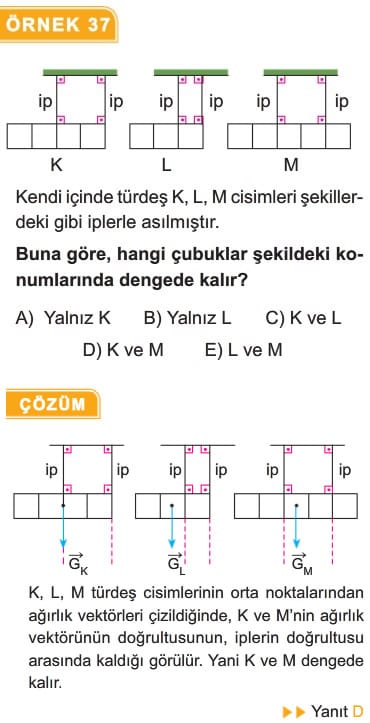
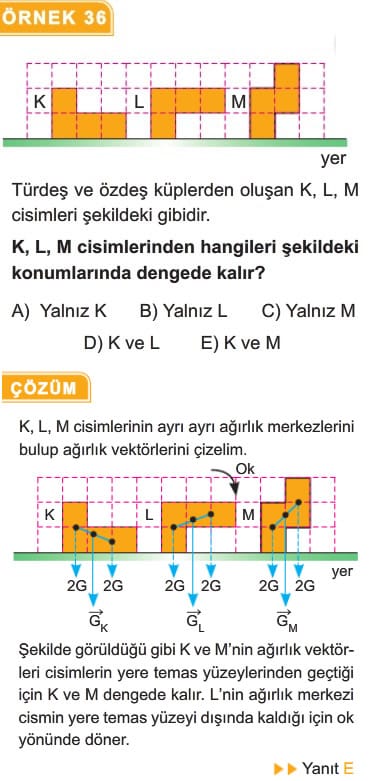
1. Düz bir zemin üzerinde duran cismin, dengede kalabilmesi için ağırlık merkezinin düşey doğrultusunun taban alanından geçmesi gerekir.
2. Bir cismi birden fazla ip ile astığımızda dengede kalabilmesi için; cismin ağırlık merkezinin ya iplerin doğrultuları arasında ya da en az bir ipin doğrultusunda olması gerekir.
