Kenarortay Alan Özellikleri Ağırlık Merkezi İlişkisi konu anlatımı çözümlü sorular matematik tyt

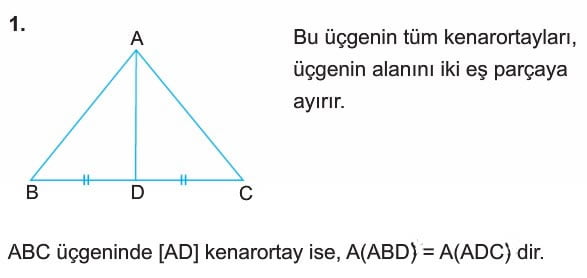
- Bir üçgenin tüm kenarortayları üçgeni iki eş parçaya ayırırlar. ABC üçgeninde AD kenarortay ise, ABD ve ADC üçgenlerinin alanları birbirine eşittir.
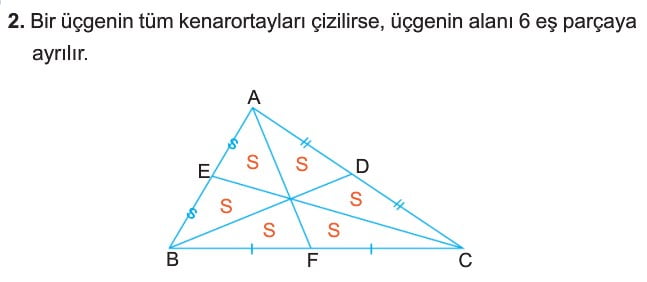
- Bir üçgenin tüm kenarortayları çizilirse üçgenin alanı 6 eş parçaya ayrılır.
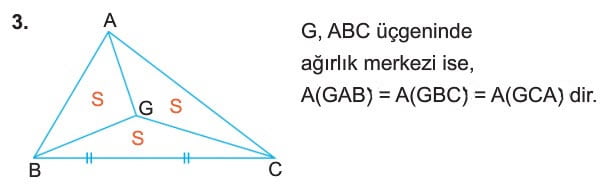
- G ABC üçgeninde ağırlık merkezi ise şekildeki üç alan da birbirine eşittir.
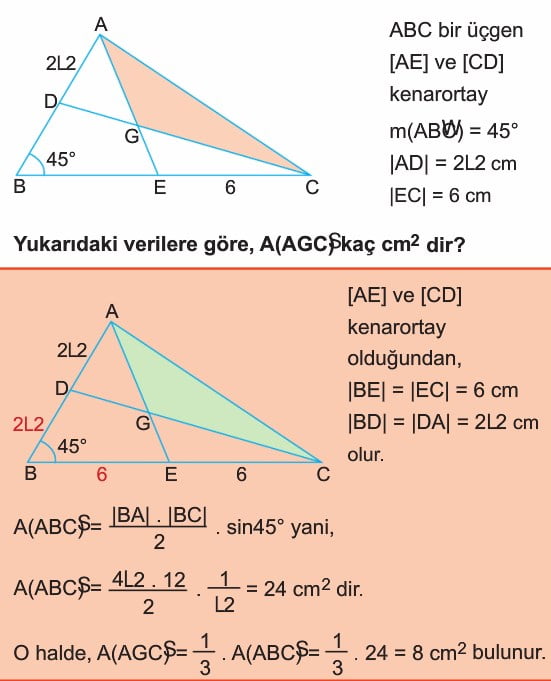
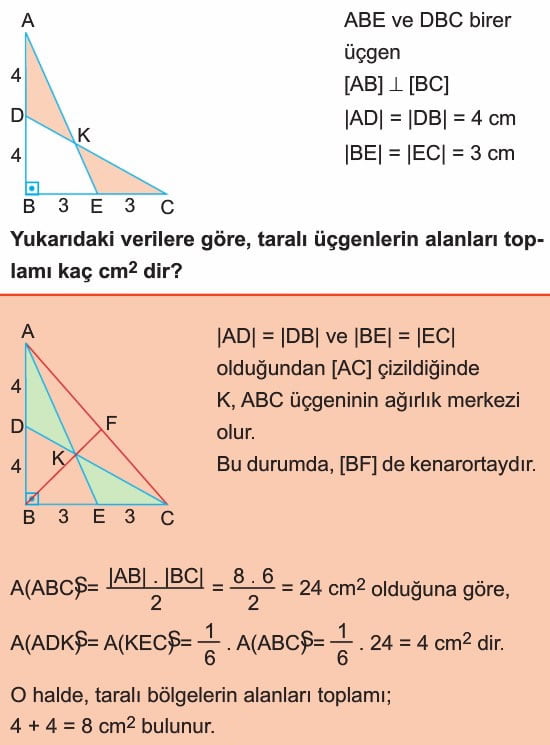
Çözüm 1: ABC üçgeinin alanı sinüs formülünden AB uzunluğu çarpı BC uzunluğu çarpı sinüs 45 bölü 2 kuralı ile bulursa alan 24 cm kare bulunur. Buradan Taralı bölgelerin alanları toplamı da 8 cm kare çıkar.
Çözüm 2: AD ve DB uzunluğu eşit, BE ve EC uzunluğu da kendi aralarında eşit olduklarından dolayı A ve C noktalarını birleştirdiğimizde oluşan ABC üçgeninin ağırlık merkezi K noktası olur. ABC üçgeni dik üçgen olduğundan dolayı alanı 8 çarpı 6 bölü 2 den 24 cm kare bulunur. Taralı alanlar kenarortayların ayırdığı 6 parçadan ikisi olduğundan dolayı sonuç 24 çarpı 2 bölü 6 dan 8 cm kare bulunur.
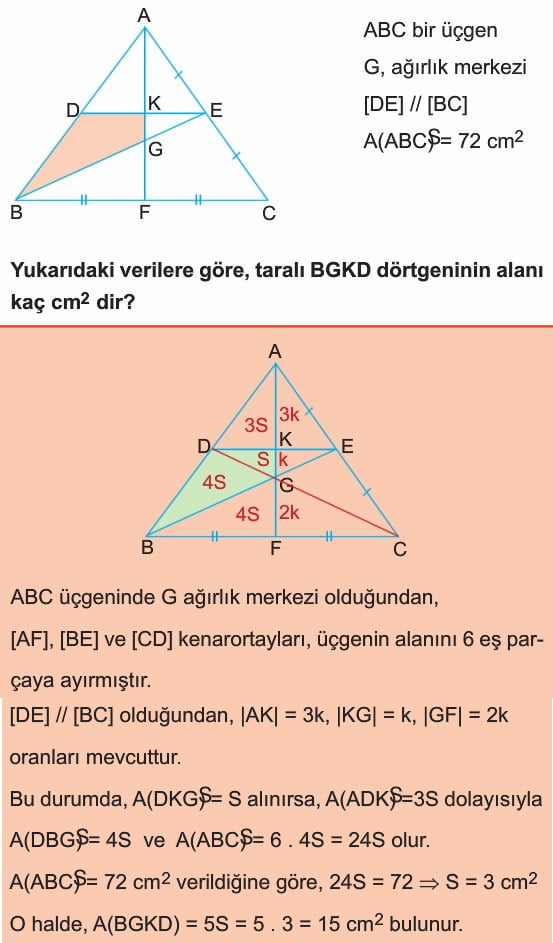
Çözüm 3: ABC üçgeninde G ağırlık merkezi olduğundan, AF, BE ve CD kenarortayları üçgenin alanı 6 eş parçaya ayırmışlardır. DE ve BC doğru parçaları birbirine paralel olduklarından, AK = 3k, KG = k, GF = 2k oranları mevcuttur. Bu durumda DKG üçgenini alanına S denirse, ADK üçgeninin alanı 3S olur ve dolayısıyla DBG üçgeninin alanı 4S ve ABC üçgeinin alanı 24S olur. ABC nin alanı 72 cm kare olduğuna göre S 3 cm karedir. Buradan BGKD dörtgeninin alanı 5S olup 5 çarpı 3 ten 15 cm kare olarak bulunur.