Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Test Çöz 9. Sınıf Matematik
Gerçek sayılar kümesi, matematikteki en geniş sayı kümelerinden biridir. Sayı doğrusunda tanımlanmış tüm rasyonel ve irrasyonel sayıları kapsar. Bu sayı aralıkları üzerinde çeşitli matematiksel işlemler yaparak, birçok problemi çözebiliriz. Gerçek sayı aralıkları, öğrencilerin matematiksel kavramları anlamaları açısından önemli bir konudur. Bu yazıda, gerçek sayı aralıkları ve aralıklar üzerinde yapılan temel işlemler ile ilgili test soruları sunacağız.
Bu yazımızda Gerçek Sayılar Kümesinde Aralık Kavramı soru çözümleri yer almaktadır. Konu hakkında bilgi eksikliğiniz varsa soru çözümlerinden önce Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Konu Anlatımı yazımıza bakmanızı tavsiye ederiz.
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Testler (Yeni Müfredat)
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Test 1 Çöz
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Test 2 Çöz
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Test 3 Çöz
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Test 4 Çöz
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Test 5 Çöz
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Test 6 Çöz
Gerçek Sayı Aralıkları ve Sayı Aralıklarında İşlemler Çözümlü Sorular (Yeni Müfredat)
Çözümlü Test Soruları
Soru 1:
Bir çiftçi, yeni ekim yapacağı tarlaların genişliklerini belirlemek istiyor. Genişlikler 5 metre ile 10 metre arasında olmalıdır. Ancak çiftçi, ekim yapacağı tarlaların genişliklerinin en az 6 metre ve en fazla 9 metre olmasını istiyor. Çiftçinin belirlediği tarlaların genişlik aralığı nedir?
A) 5 < x < 10
B) 6 ≤ x ≤ 9
C) 6 < x < 9
D) 5 ≤ x ≤ 10
Çözüm: Çiftçinin belirlediği genişliklerin en az 6 metre ve en fazla 9 metre olmasını istiyor, bu durumda aralık kapalı bir aralık olur. Yani 6 metre ve 9 metre değerleri dahil edilir. Bu nedenle doğru cevap, 6 ile 9 arasında kapalı bir aralık olan 6 ≤ x ≤ 9‘dur. Doğru cevap: B)
Soru 2:
Bir öğrenci, matematik dersinde verilen sayı aralıklarını incelemektedir. Öğrencinin çalıştığı aralıklar sırasıyla 2 ile 7 arasında (2 dahil değil, 7 dahil) ve 4 ile 9 arasında (her iki uç nokta dahil). Bu iki aralığın kesişim kümesi nedir?
A) (2, 7]
B) (4, 7]
C) [4, 7]
D) [2, 7]
Çözüm: Verilen iki aralığın kesişim kümesi, ortak elemanların bulunduğu bölgedir. İlk aralık 2 < x ≤ 7, ikinci aralık ise 4 ≤ x ≤ 9’dur. İki aralığın kesişimi, 4 ile 7 arasındaki değerlerdir ve 4 ve 7 dahil olduğu için kesişim kümesi [4, 7] olur. Doğru cevap: C)
Soru 3:
Bir asansör, ağırlık sınırı olarak 500 kg ile 1000 kg arasında bir yük taşıyabilmektedir. Fakat güvenlik nedeniyle asansörün kapasitesini 600 kg ile 900 kg arasında sınırlamak istenmektedir. Bu sınırlamalara göre asansörün taşıyabileceği ağırlık aralığı nedir?
A) (500, 1000)
B) [600, 900]
C) (600, 900)
D) [500, 1000]
Çözüm: Asansörün taşıyabileceği güvenli ağırlık aralığı 600 kg ile 900 kg arasında, bu nedenle sınırlar dahil edilerek belirlenen aralık [600, 900] olacaktır. Yani hem 600 kg hem de 900 kg değerleri kapsanır. Doğru cevap: B)
Soru 4:
Bir şirkette çalışanların maaşları 3000 TL ile 5000 TL arasında değişmektedir. Ancak şirket yönetimi, çalışanların maaşlarının en fazla 4500 TL olmasını istemektedir. Bu durumda maaşların yeni aralığı nedir?
A) [3000, 5000]
B) (3000, 5000)
C) [3000, 4500]
D) (3000, 4500]
Çözüm: Şirket yönetimi, maaşların en fazla 4500 TL olmasını istediği için maaşlar 3000 TL ile 4500 TL arasında olacak ve bu değerler dahil edilecektir. Bu durumda, aralık [3000, 4500] olarak ifade edilir. Doğru cevap: C)

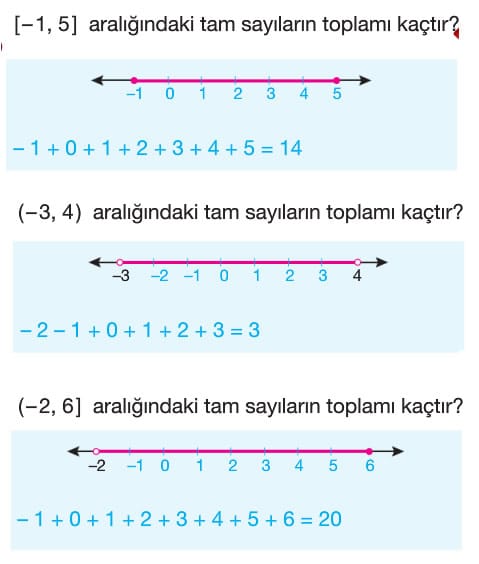

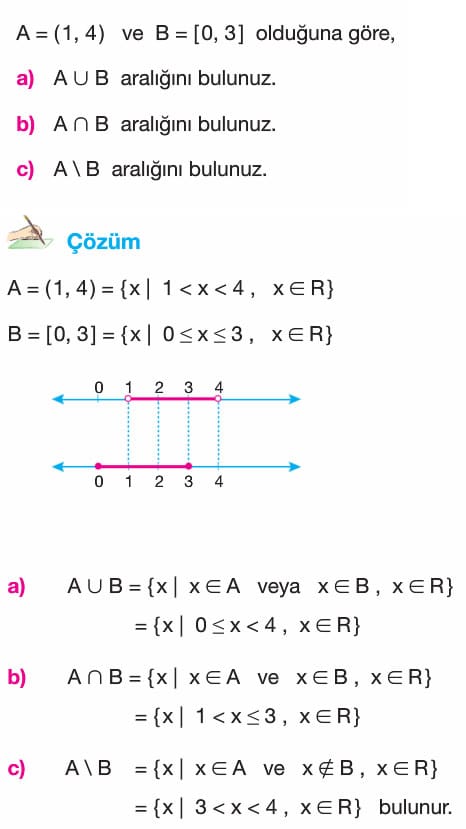


Ya sınavda bu tarz değilde daha grafikleri çıkıyo grafikleri olsa güzel olur
bence daha fazla yeni müfredat sorusu gelmeli. Soru bulamıyoruz yeni mufredatla ilgili.
sayenizde çok iyi öğreniyorum