Doğrusal İlişkiler 8. Sınıf
İki değişken arasındaki ilişkinin grafiği doğru şeklinde ise bu iki değişken arasında doğrusal ilişki vardır. Doğrusal ilişkiyi ifade eden denklemlere de doğrusal denklem denir.
Dikkat: Bağımlı değişken başka bir değişken cinsinden tanımlanan değişkendir. Bağımsız değişken ise başka bir değişkeni tanımlayan değişkendir.
Önemli Bilgi: Doğrusal ilişki, iki değişkenden oluşan ax + by + c = 0 biçimindeki cebirsel ifade ile gösterilebilir. Bu ifadede c sabit sayı, a ve b katsayılardır. a ile b aynı anda sıfır olamaz.
Hatırlayalım: İki değişkenden birincisi, ikincisine bağlı olarak değişiyorsa birinci değişkene bağımlı değişken, ikinci değişkene bağımsız değişken denir.
Doğrusal İlişkiler 8. Sınıf konu anlatımı Lgs Çözümlü Sorular
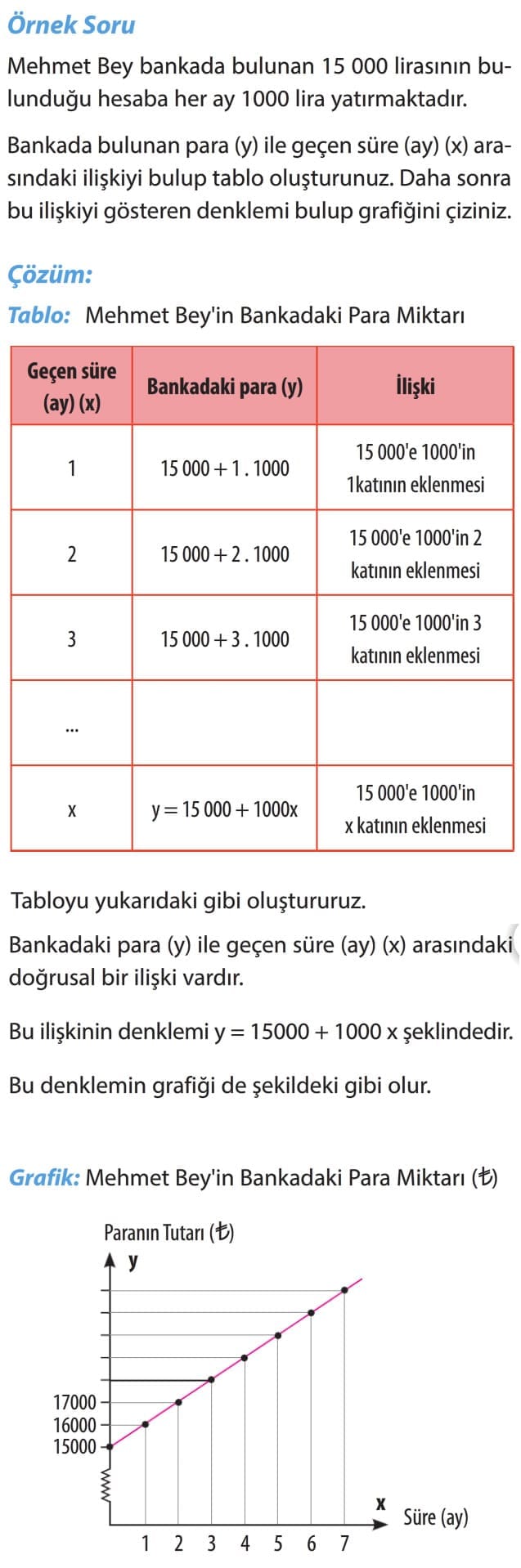
Örnek Soru: Mehmet Bey bankada bulunan 15 000 lirasının bulunduğu hesaba her ay 1000 lira yatırmaktadır. Bankada bulunan para (y) ile geçen süre (ay) (x) arasındaki ilişkiyi bulup tablo oluşturunuz. Daha sonra bu ilişkiyi gösteren denklemi bulup grafiğini çiziniz.
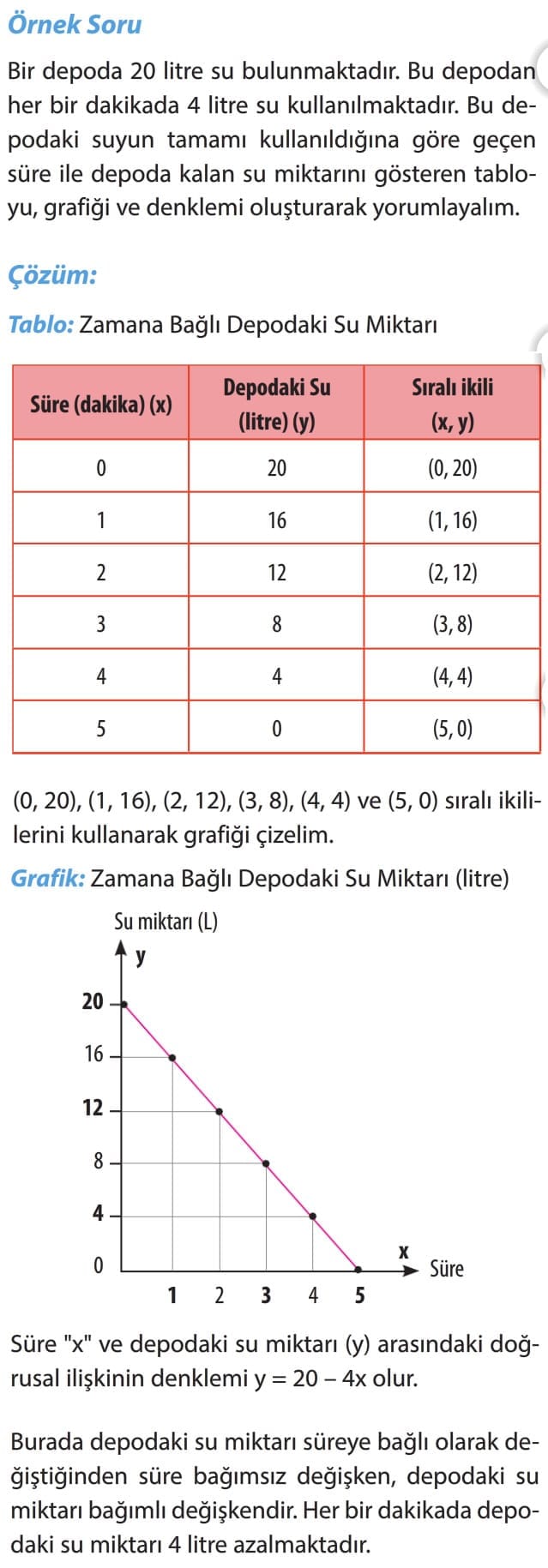
Örnek Soru: Bir depoda 20 litre su bulunmaktadır. Bu depodan her bir dakikada 4 litre su kullanılmaktadır. Bu depodaki suyun tamamı kullanıldığına göre geçen süre ile depoda kalan su miktarını gösteren tabloyu, grafiği ve denklemi oluşturarak yorumlayalım.
Çözüm: (0, 20), (1, 16), (2, 12), (3, 8), (4, 4) ve (5, 0) sıralı ikililerini kullanarak grafiği çizelim. Süre "x" ve depodaki su miktarı (y) arasındaki doğrusal ilişkinin denklemi y = 20 - 4x olur. Burada depodaki su miktarı süreye bağlı olarak değiştiğinden süre bağımsız değişken, depodaki su miktarı bağımlı değişkendir. Her bir dakikada depodaki su miktarı 4 litre azalmaktadır.
Örnek Soru: Sınava hazırlanan bir öğrenci günde 50 soru çözerken daha sonraki günlerde çözdüğü soru sayısını her gün 10 artırmıştır. Soru sayısı (y) ile geçen süre (x) arasındaki ilişkiyi gösteren denklemi bulup grafiğini çizelim.
Örnek Soru: Günde 5 litre su tüketen bir ailenin bir haftalık su tüketimini tablo ve grafik ile gösterelim.
Çözüm: (1, 5), (2, 10), (3, 15), (4, 20), (5, 25), (6, 30) ve (7, 35) sıralı ikililerinden faydalanarak grafiği çizelim. Yukarıdaki grafikte görüldüğü gibi her bir gün ile tüketilen su miktarı arasında doğrusal bir ilişki vardır. Sıralı ikililerin birleştirilmesiyle oluşan grafik doğrusal şekilde olmuştur. Bu ilişkinin denklemi y = 5x'tir. Burada günler ile tüketilen su miktarı arasındaki ilişki incelendiğinde, tüketilen su miktarı gün sayısı ile değişmektedir. Yani tüketilen su miktarı gün sayısına bağlıdır. Bundan dolayı tüketilen su miktarı bağımlı değişken, gün sayısı bağımsız değişkendir.