Doğruların Yolculuğu (Doğruların Durumlarına Göre Oluşan Açılar) 5. Sınıf Matematik (Yeni Müfredat)

Kategoriler: 5. Sınıf Matematik Konuları, Konu Anlatımları, Matematik
Cepokul

Matematiğin önemli bir dalı olan geometri, şekillerin, çizgilerin ve yüzeylerin özelliklerini anlamamıza yardımcı olur. Bu yolculukta, doğru kavramı ve doğruların birbirleriyle olan ilişkileri önemli bir yer tutar. 5. sınıf seviyesinde öğrenciler, iki doğrunun nasıl kesiştiğini, çakıştığını veya paralel olduğunu keşfederler. Bu makale, doğruların nasıl bir araya geldiklerini ve aralarındaki ilişkileri öğrenmek isteyen öğrenciler için rehber niteliğindedir.

5. Sınıf 1. Tema: Geometrik Şekiller Konu Anlatımları (2024 – 2025 Yeni Müfredat)

5. Sınıf Doğruların Yolculuğu Testleri

5. Sınıf Doğruların Yolculuğu Ders Notu (Yeni Müfredat)

İki Doğrunun Kesişimi

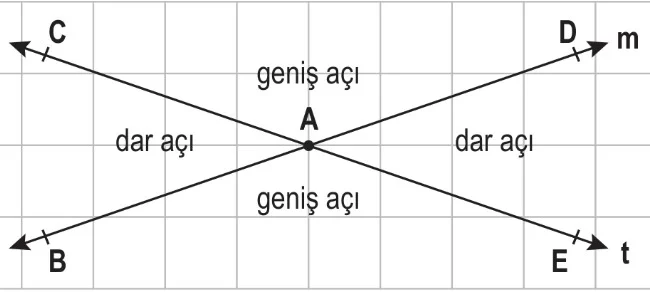
  • Düzlemde verilen m ve t doğrularının ortak noktası A’dır. Ortak noktası bulunan doğrulara kesişen doğrular denir.
  • Kesişen doğrular açılar meydana getirir.
    ve dar açıları ile ve geniş açıları t ve m doğrularının A noktasında kesişimi ile oluşmuşlardır.

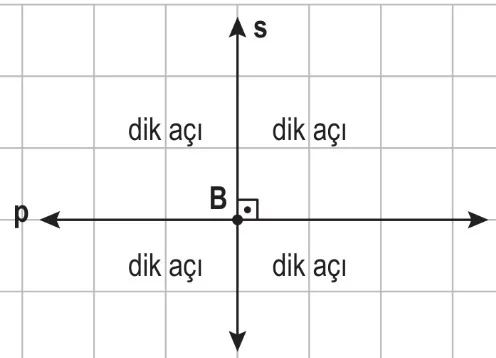
s ve p doğrularının kesişimiyle dört tane dik açı oluşabilir. Kesişimiyle dik açı oluşturan doğrulara dik kesişen doğrular denir ve p ⊥ s şeklinde gösterilir.

Düzlemde Açı Oluşturmayan Doğrular (Paralel Doğrular)

Düzlemde verilen d ve m doğrularının ortak noktası olmadığından herhangi bir açı oluşturmaz. Ortak noktası olmayan doğrulara paralel doğrular denir ve d // m şeklinde gösterilir.

İki Doğrunun Çakışması

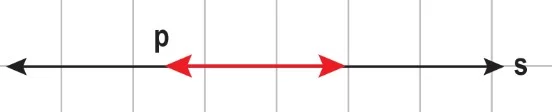
p doğrusunun bütün noktaları aynı zamanda s doğrusunun elemanları olup bu durumdaki doğrulara çakışık doğrular denir. Çakışık doğrular açı oluşturmazlar.

Komşu Açı ve Ters Açı

Köşesi ve birer ışını ortak olan ancak iç bölgeleri ortak olmayan açılara komşu açılar denir.

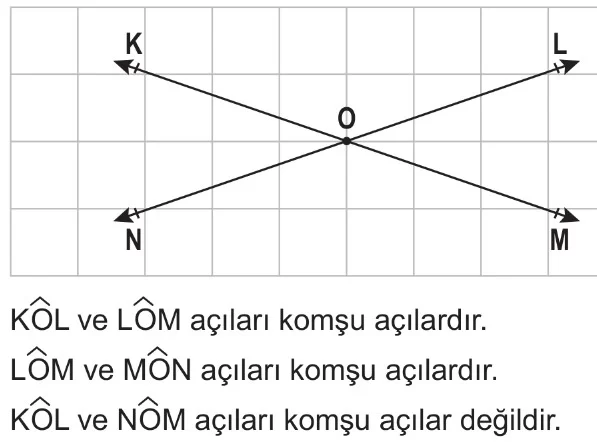
Kesişen iki doğru üzerinde oluşan açılarda komşu olmayan açılara ters açı denir. Ters açıların ölçüleri birbirine eşittir.

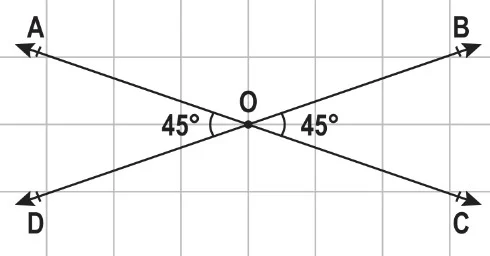
A noktasında kesişen doğru parçaları ile ters açılar oluşturulmuştur.

  • ile ters açılardır.
  • ile ters açılardır.
  • Ters açıların ölçüleri eşittir.
    = = 45°

Üç Doğrunun Paralelliği

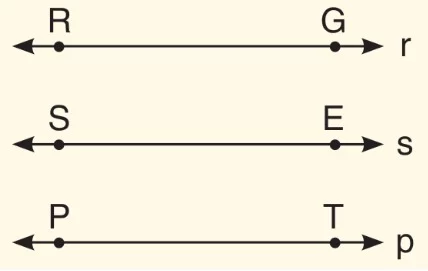
Yukarıdaki doğrular sembolle RG // SE // PT veya r // s // p şeklinde yazılır.

Üç Doğrunun Bir Noktada Kesişimi

  • Ölçüleri toplamı 90° olan iki açıya tümler açılar denir.
  • Köşeleri ve birer kolları ortak olan açılara komşu açılar denir.
  • Ölçüleri toplamı 90° olan komşu açılara komşu tümler açılar denir.
  • Ölçüleri toplamı 180° olan açılara bütünler açılar denir.
  • Ölçüleri toplamı 180° olan komşu açılara komşu bütünler açılar denir.

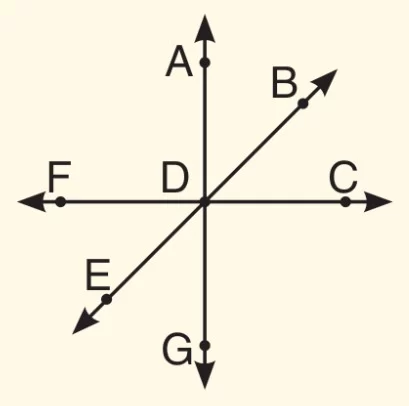
  • ADB ile EDG ters açılara,
  • BDC ile CDG komşu açılara,
  • EDG ile FDE komşu tümler açılara,
  • FDB ile BDC komşu bütünler açılara örnek olarak verilebilir.

Üç Doğrunun İkişer İkişer Kesişimi

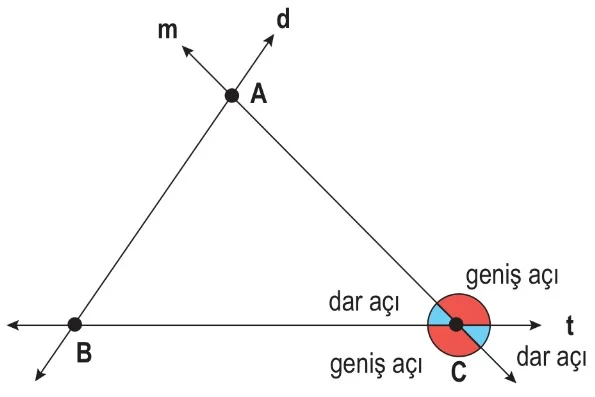
  • d ile m doğruları A noktasında, t ile m doğruları C noktasında, t ile d doğruları B noktasında kesişebilirler.
  • A, B, C noktalarında dar, dik veya geniş açılar oluşabilir. Örneğin, , gibi.
  • Mavi ve kırmızı renkli açılar aynı zamanda komşu bütünler açılardır.

İki Paralel Doğru ve bir Kesen

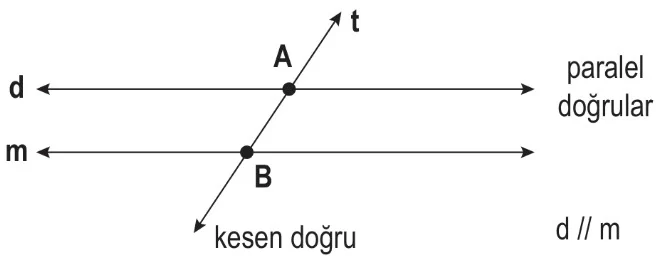
  • d ve m paralel doğrular olup t doğrusu d ve m doğrularını kesen durumundadır.
  • İki paralel doğruyu kesen doğru çeşitli açılar oluşturur.
  • Oluşan bu açılardan geniş açılar ve dar açılar ters açı olduklarından kendi aralarında eş ölçüye sahiptirler.

Örneğin;

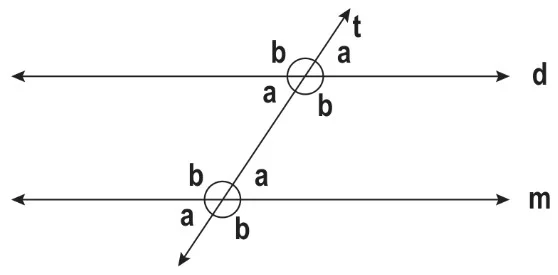
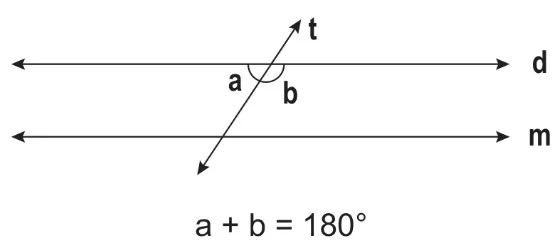
a açıları dar açı ve b açıları geniş açı olup kendi aralarında eşittir. Aynı zamanda a ile b açılarının toplamı 180° olduğu için bütünler açılardır.

İki paralel doğrunun keseni dik açı oluşturabilir.

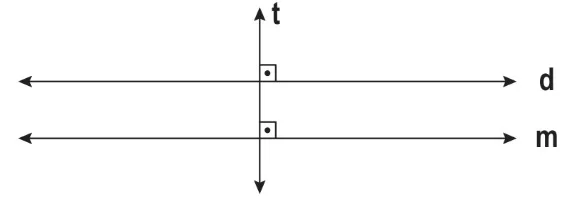
Bu durumda 8 tane dik açı oluşturur.

Örnek: Aşağıdaki iki paralel doğruya bir kesenle yapılan çizimlerde oluşan açılar görülmektedir.

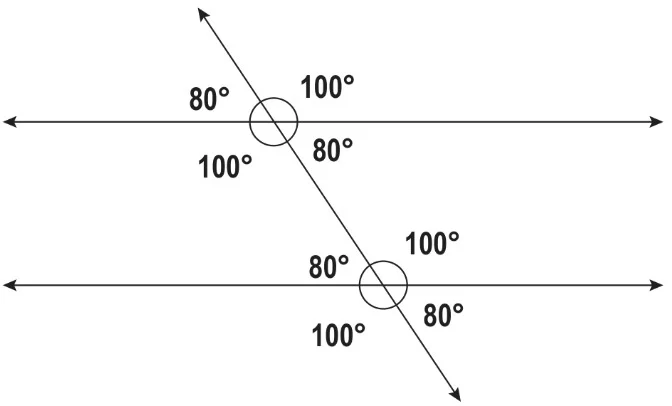
Çizimde dört tane dar açı ve dört tane geniş açı oluştuğu görülmektedir.

İki Doğrunun Kesişimi

İki doğru aynı düzlemde olup bir noktada buluştuğunda bu doğrular kesişen doğrular olarak adlandırılır. Kesişen doğrular bir açı oluşturur ve bu açı, doğruların birbirlerine göre eğimini gösterir. Bu durumda doğrular, birbirlerinden farklı doğrultularda hareket ederler. Örneğin, bir artı işareti gibi iki doğru birbirini dik açıyla kesebilir.

Düzlemde Açı Oluşturmayan Doğrular

Bazı doğrular düzlemde hiçbir ortak noktada buluşmazlar ve açı oluşturmazlar. Bu doğrular ya birbirine paraleldir ya da birbirinden tamamen bağımsızdır. Paralel doğrular, aralarındaki mesafe sabit olan ve sonsuza kadar uzasalar bile asla kesişmeyen doğrulardır. Eğer doğrular aynı düzlemde değilse, bu doğruların birbirini kesmesi veya açı oluşturması mümkün değildir.

İki Doğrunun Çakışması

İki doğru, her noktada aynı doğrultuda ilerliyorsa ve tüm noktaları aynıysa bu doğrulara çakışık doğrular denir. Çakışık doğrular, aynı düzlemde bulunur ve birbirinin üzerine binerler. Bu durumda, bir doğru diğerinin tamamen üzerine oturduğu için iki doğru gibi değil, tek bir doğru gibi görünür.

Üç Doğrunun Paralelliği

Eğer üç doğru birbirine paralel olursa, bu doğruların her biri arasında sabit bir mesafe bulunur. Üç paralel doğru, birbirlerine hiçbir noktada değmezler ve birbirlerini kesmezler. Bu doğrular düz bir çizgi gibi aynı yönde ilerler ve sonsuza kadar devam eder. Örneğin, demiryolu rayları üç paralel doğru gibi düşünülebilir.

Üç Doğrunun Bir Noktada Kesişimi

Üç doğru aynı noktada kesiştiğinde bu durum, üç doğru arasındaki bir kesişim noktası oluşturur. Bu tür bir kesişim, bir nokta üzerinde toplanan farklı doğruların bir araya geldiğini gösterir. Örneğin, bir köşede birleşen üç yol bu duruma benzer.

Üç Doğrunun İkişer İkişer Kesişimi

Üç doğru, ikişer ikişer farklı noktalarda kesişebilir. Bu durumda üç doğru birbirinden bağımsız olarak iki noktada kesişir. Her iki doğru farklı bir kesişim noktası oluşturur ve bu noktalar farklı açılarla ifade edilir. İkişer ikişer kesişen doğrular, şekil oluşturma ve geometrik yapıların temelini oluşturur.

İki Paralel Doğru ve Bir Kesen

İki paralel doğru birbirine asla değmeyen ve sabit mesafede ilerleyen doğrulardır. Bu doğrulara bir kesen doğru eklendiğinde, paralel doğrular üzerinde çeşitli açılar oluşur. Paralel doğrularla kesişen bu doğru, kesişme noktasında dar veya geniş açılar oluşturabilir. Örneğin, yolun iki kenarı boyunca uzanan kaldırım taşları ve bunları dikine kesen bir yol bu duruma örnek verilebilir.

Liselere Giriş Sınavı (LGS)
5 Haziran 2022 Pazar
Temel Yeterlilik Sınavı (TYT)
18 Haziran 2022 Cumartesi
Alan Yeterlilik Sınavı (AYT)
19 Haziran 2022 Pazar