Bir Noktanın Doğruya Olan Uzaklığı 11. Sınıf
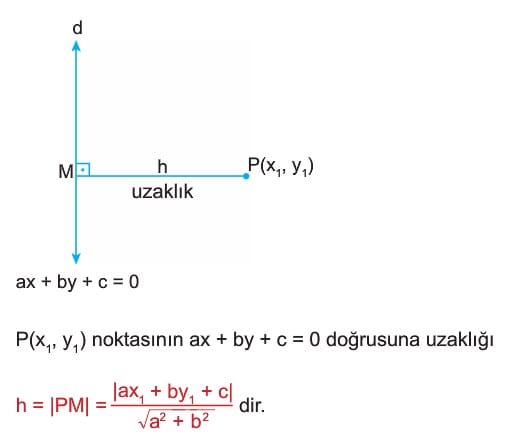
Bir Noktanın Bir Doğruya Olan Uzaklığı
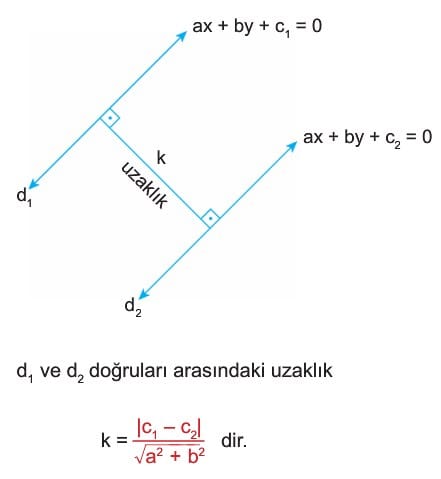
Paralel İki Doğru Arasındaki Uzaklık
Bilgi: İki doğru arasındaki uzaklığı bulabilmek için her iki doğru denklemindeki x lerin katsayıları eşit ve y lerin katsayıları eşit olmalıdır. Yani sadece paralel iki doğru arasındaki uzaklık bulunabilir. Doğrular paralel olduğu halde katsayılar eşit değilse katsayılar eşitlendikten sonra formül uygulanmalıdır.
Bir Noktanın Doğruya Olan Uzaklığı – 11. Sınıf Çözümlü Test Soruları
Soru 1 (Yeni Nesil Soru):
Bir futbol sahasının iki kale direği A ve B noktalarıdır. Kale direklerinden biri olan A noktasının koordinatları (3, 6) ve orta çizgiyi gösteren doğrunun denklemi 4x – 5y + 20 = 0 olarak veriliyor. A noktasının bu doğruya olan uzaklığını bulunuz.
A) 1 birim
B) 2 birim
C) 3 birim
D) 4 birim
E) 5 birim
Çözüm:
Bir noktanın doğruya olan uzaklığı formülü şu şekildedir:
Uzaklık (d) = |Ax₁ + By₁ + C| / √(A² + B²)
Verilen doğru denklemi 4x – 5y + 20 = 0. Burada A = 4, B = -5 ve C = 20’dir. Nokta A(3, 6) olduğuna göre x₁ = 3 ve y₁ = 6.
Formülde yerine koyarsak:
d = |4(3) + (-5)(6) + 20| / √(4² + (-5)²)
d = |12 – 30 + 20| / √(16 + 25)
d = |2| / √41
d ≈ 2 / 6.4
d ≈ 0.31 birim
Cevap: A
Soru 2:
Nokta B(2, -1) ve doğru denklemi x – y – 1 = 0 verilmiştir. B noktasının bu doğruya olan uzaklığını bulunuz.
A) √2
B) 2√2
C) 1
D) 2
E) 3
Çözüm:
Doğru denklemi x – y – 1 = 0. Burada A = 1, B = -1 ve C = -1’dir. Nokta B(2, -1) olduğuna göre x₁ = 2 ve y₁ = -1.
Formülde yerine koyarsak:
d = |1(2) + (-1)(-1) – 1| / √(1² + (-1)²)
d = |2 + 1 – 1| / √(1 + 1)
d = |2| / √2
d = 2 / √2
d = √2
Cevap: A
Soru 3 (Yeni Nesil Soru):
Bir gökdelen projesinde, binanın bir köşesi C noktası (4, -3) koordinatlarında yer alıyor. Binanın inşaat hattı ise x + 2y + 5 = 0 doğrusu ile gösteriliyor. Bu noktadan inşaat hattına olan mesafenin, güvenlik standartlarına göre en az 3 birim olması gerekiyor. Bu durum sağlanıyor mu? Eğer sağlanmıyorsa, kaç birim daha uzaklaştırılmalı?
A) 0.5 birim
B) 1 birim
C) 1.5 birim
D) 2 birim
E) Güvenlik şartı sağlanmıştır
Çözüm:
Noktanın doğruya olan uzaklığı formülünden yola çıkarak:
Doğru denklemi: x + 2y + 5 = 0
Burada A = 1, B = 2 ve C = 5’dir. Nokta C(4, -3) olduğuna göre x₁ = 4 ve y₁ = -3.
d = |1(4) + 2(-3) + 5| / √(1² + 2²)
d = |4 – 6 + 5| / √(1 + 4)
d = |3| / √5
d ≈ 3 / 2.24
d ≈ 1.34 birim
Güvenlik standardı en az 3 birim mesafe olduğuna göre, 3 – 1.34 = 1.66 birim daha uzaklaştırılması gerekmektedir.
Cevap: C
Soru 4:
Nokta D(1, 2) ve doğru denklemi 3x – 4y + 7 = 0 verilmiştir. D noktasının bu doğruya olan uzaklığını bulunuz.
A) 0.5
B) 1
C) 1.5
D) 2
E) 2.5
Çözüm:
Formül: Uzaklık (d) = |Ax₁ + By₁ + C| / √(A² + B²)
Doğru denklemi 3x – 4y + 7 = 0 olduğuna göre, A = 3, B = -4 ve C = 7’dir. Nokta D(1, 2) için x₁ = 1 ve y₁ = 2.
d = |3(1) – 4(2) + 7| / √(3² + (-4)²)
d = |3 – 8 + 7| / √(9 + 16)
d = |2| / √25
d = 2 / 5
d = 0.4
Cevap: A
Soru 5:
Nokta E(-1, 5) ve doğru denklemi 2x – y + 3 = 0 verilmiştir. E noktasının bu doğruya olan uzaklığını bulunuz.
A) 1 birim
B) 2 birim
C) 3 birim
D) 4 birim
E) 5 birim
Çözüm:
Doğru denklemi 2x – y + 3 = 0 olduğuna göre A = 2, B = -1 ve C = 3. Nokta E(-1, 5) için x₁ = -1 ve y₁ = 5.
d = |2(-1) – 1(5) + 3| / √(2² + (-1)²)
d = |-2 – 5 + 3| / √(4 + 1)
d = |-4| / √5
d = 4 / √5
Yaklaşık olarak d ≈ 1.79 bulunur.
Cevap: B