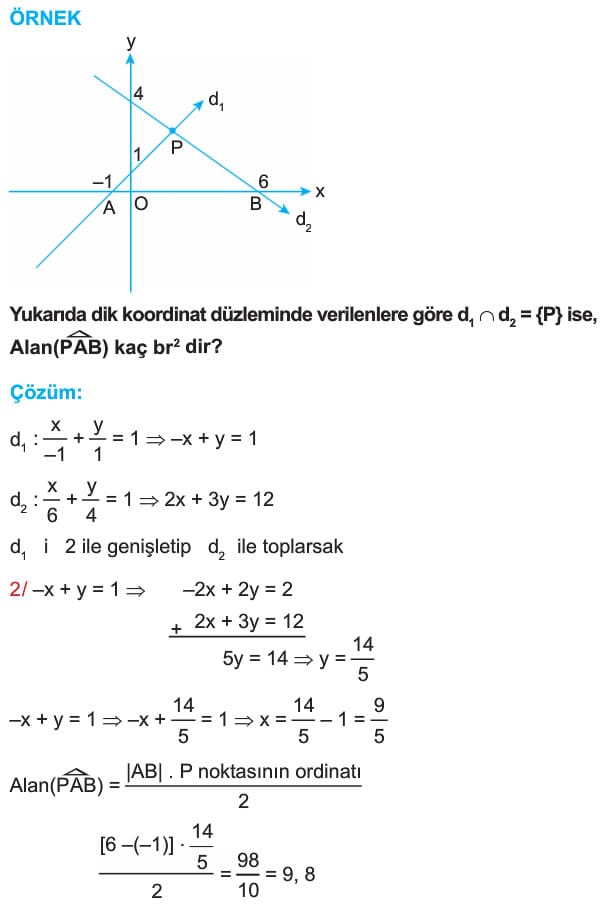
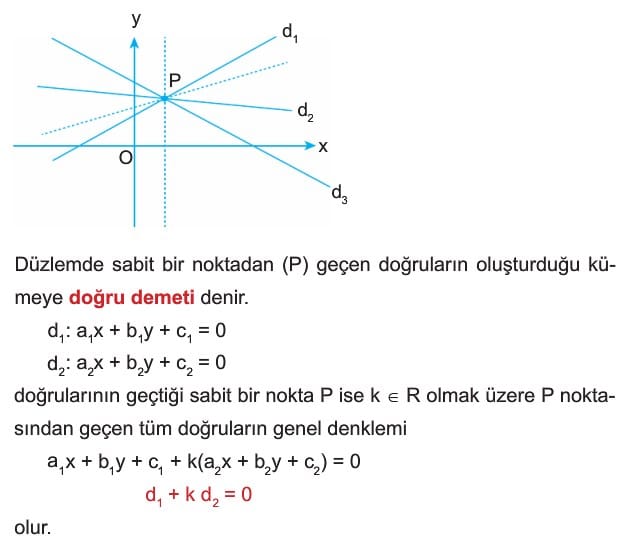
İki Doğrunun Birbirine Göre Durumları 11. Sınıf
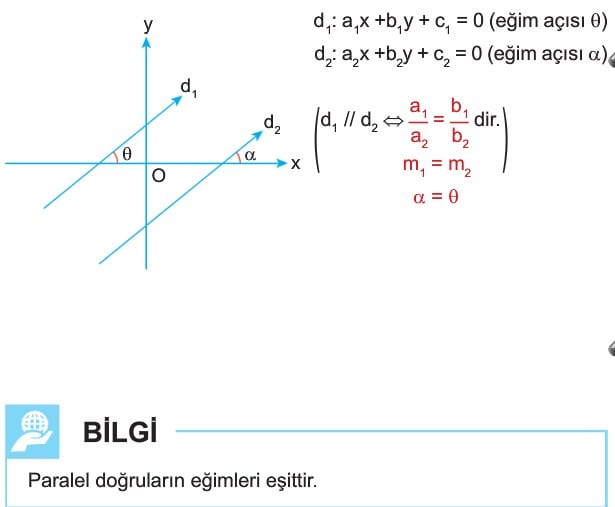
Paralel Doğrular
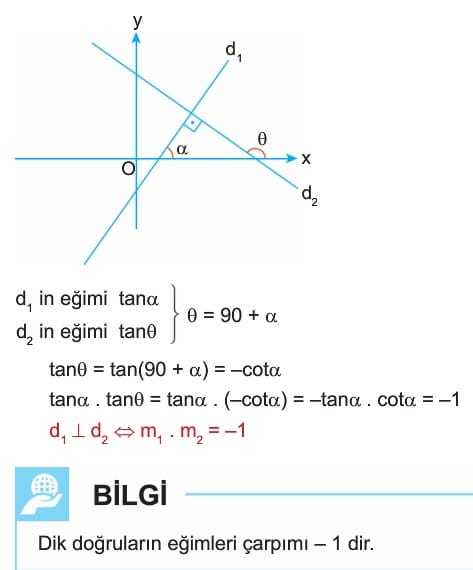
Dik Doğrular
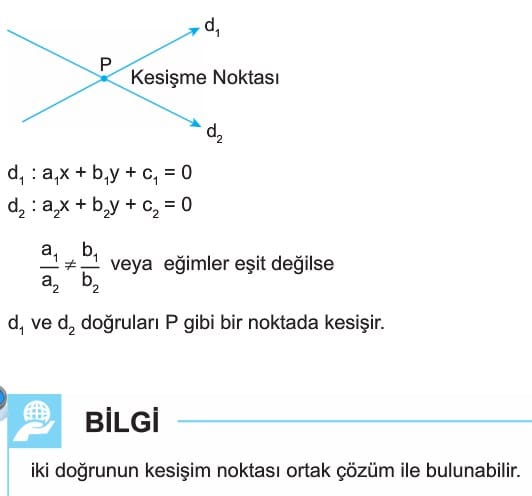
Kesişen Doğrular
Çakışık Doğrular
Doğru Demeti
Çözümlü Örnek Test Soruları
Soru 1:
D1: 2x – 3y + 6 = 0 ve D2: 4x – 6y – 9 = 0 doğruları için, bu doğruların birbirine göre durumu nedir?
A) Paralel
B) Dik
C) Kesişen
D) Çakışık
E) Belirlenemez
Çözüm:
Doğruların eğimlerini bulmak için denklemleri y = mx + b formuna getirelim:
- D1: 2x – 3y + 6 = 0 → y = (2/3)x + 2
- D2: 4x – 6y – 9 = 0 → y = (2/3)x + 1.5
Eğilimleri aynı olduğundan, doğrular paraleldir. Cevap: A) Paralel
Soru 2:
D1: y = 3x + 5 ve D2: y = -1/3 x + 7 doğruları için, bu doğruların birbirine göre durumu nedir?
A) Paralel
B) Dik
C) Kesişen
D) Çakışık
E) Belirlenemez
Çözüm:
D1’in eğimi m1 = 3, D2’nin eğimi m2 = -1/3’tür.
m1 * m2 = 3 * (-1/3) = -1 olduğundan, doğrular birbirine diktir.
Cevap: B) Dik
Soru 3:
D1: y = -2x + 1 ve D2: y = -2x – 3 doğruları için, doğruların birbirine göre durumu nedir?
A) Paralel
B) Dik
C) Kesişen
D) Çakışık
E) Belirlenemez
Çözüm:
Her iki doğrunun da eğimi -2 olduğundan, doğrular paraleldir. Ancak y-eksenini kestikleri noktalar farklı olduğu için çakışık değillerdir.
Cevap: A) Paralel
Soru 4:
D1: 3x + 4y – 12 = 0 ve D2: 6x + 8y + 16 = 0 doğruları için doğruların durumu nedir?
A) Paralel
B) Dik
C) Kesişen
D) Çakışık
E) Belirlenemez
Çözüm:
D1’in eğimi: y = -3/4 x + 3
D2’nin eğimi: y = -3/4 x – 2
Eğimler aynı, ancak y-eksenini kestikleri noktalar farklı. Bu nedenle doğrular paraleldir. Cevap: A) Paralel
Soru 5:
D1: 2x – y + 3 = 0 ve D2: x + 2y – 5 = 0 doğrularının eğimlerinin çarpımı -1 olduğuna göre, doğruların birbirine göre durumu nedir?
A) Paralel
B) Dik
C) Kesişen
D) Çakışık
E) Belirlenemez
Çözüm:
D1: y = 2x + 3 (eğim = 2)
D2: y = -1/2 x + 5/2 (eğim = -1/2)
Eğim çarpımı: 2 * (-1/2) = -1 olduğu için doğrular diktir.
Cevap: B) Dik
Soru 6:
D1: y = 5x + 6 ve D2: y = 5x – 4 doğrularının durumunu belirleyin.
A) Paralel
B) Dik
C) Kesişen
D) Çakışık
E) Belirlenemez
Çözüm:
D1 ve D2’nin eğimleri aynı olduğundan doğrular paraleldir. Ancak y-eksenini kestikleri noktalar farklıdır.
Cevap: A) Paralel
Soru 7:
D1: 2x + 3y = 6 ve D2: -3x + 2y = 4 doğrularının durumu nedir?
A) Paralel
B) Dik
C) Kesişen
D) Çakışık
E) Belirlenemez
Çözüm:
Eğimler çarpımı -1 olduğundan (m1 = 2/3, m2 = -2/3), doğrular diktir.
Cevap: B) Dik
Soru 8:
D1: y = 4x – 1 ve D2: 4y = 16x – 4 doğruları için doğruların durumu nedir?
A) Paralel
B) Dik
C) Kesişen
D) Çakışık
E) Belirlenemez
Çözüm:
D2’yi y = 4x – 1 formuna getirdiğimizde D1 ile tamamen aynı doğrular olduğu görülür. Bu nedenle çakışıktırlar.
Cevap: D) Çakışık
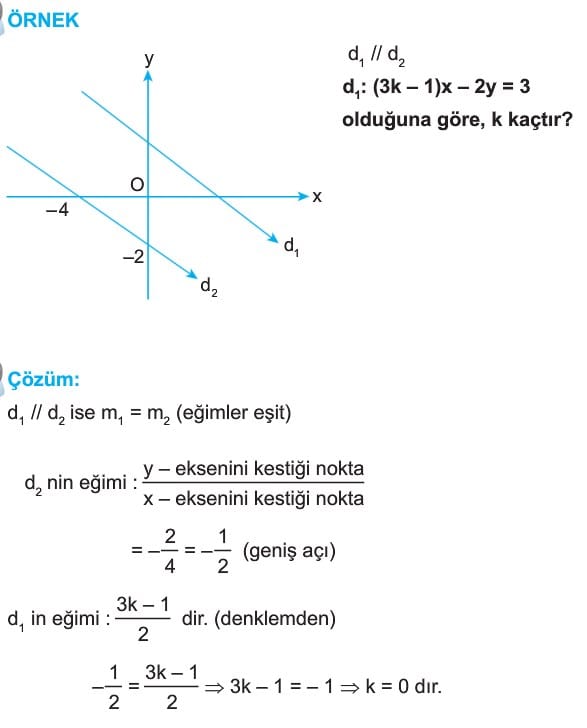
Paralel Doğrular: a1x + b1y + c1 = 0 ve a2x + b2y + c2 = 0 doğrularında a1 / b1 = a2 / b2 eşitliği sağlanıyorsa bu doğrular birbirine paralel doğrulardır. Paralel doğruların eğim açıları birbirine eşittir.
Örnek: A (2, -3) noktasından geçen ve ve y = 4x – 1 doğrusuna paralel olan doğrunun denklemini bulun.
Çözüm: y = 4x – 1 doğrusunun eğimi x in katsayısı olan 4 dür. Dolayısıyla bu doğruya paralel olan doğrunun eğimi de 4 dür. Eğimi 4 olan ve A(2, -3) noktasından geçen doğrunun denklemi, y-(-3)=4.(x-2) bağıntısından y = 4x -11 olur.
Dik Doğrular: Eğimleri m1 ve m2 olan iki doğruda m1 . m2 = -1 ise bu doğrular dikdir, yani eğimleri çarpımı -1 olan doğrular birbirlerine dikdir.
Örnek: y = 3x – 4 ve y = (2k-1)x + 6 doğruları birbirlerine dik olduklarına göre k sayısı kaçtır?
Çözüm: y = 3x-4 doğrusunun eğimi 3 ve y = (2k-1)x + 6 doğrusunun eğimi 2k-1 dir. Bu eğimlerin çarpımını -1 e eşitlersek, 3 . (2k-1) = -1 den k = 1/3 olarak bulunur.
Örnek: A(-1, 4) noktasından geçen ve 2x-3y+4=0 doğrusuna dik olan doğru denklemini bulunuz.
Çözüm: 2x-3y+4=0 doğrusunun eğimi 2 / 3 olduğundan aradığımız doğrunun eğimi -3/2 olur. Buradan eğimi -3/2 ve geçtiği nokta -1,4 olan doğrunun denklemi, y-4=-3/2 . (x+1) bağıntısından bulunur. Bağıntıyı düzenlersek doğrunun denklemi 2y+3x-5=0 olarak bulunur.
Kesişen Doğrular: a1x+b1y+c1=0 ve a2x+b2y+c2=0 doğrularında a1/a2 eşit değil b1/b2 oluyorsa bu iki doğru kesişiyordur. Kesişen doğruların kesişim noktasının koordinatlarını bulmak için iki doğru denkleminin ortak çözümü yapılır.
Örnek: 2x+3y+5=0 ve 3x-2y-4=0 doğrularının kesişim noktasının koordinatlarını bulunuz.
Çözüm: iki denklem alt alta yazılıp birinci denklem 2 ile ikinci denklem 3 ile genişletilerek taraf trafa toplanırsa y ler sadeleşir ve x = 2/13 bulunur. birinci veya ikinci denklemde bu değer yerine yazılırsa y = -69/39 bulunur.