Denklem Sistemleri (8. Sınıf)
İki farklı büyüklük arasındaki iki farklı ilişkiyi anlatan doğrusal denklem çiftine doğrusal denklem sistemi denir. İki bilinmeyenli doğrusal denklem sistemlerinin çözümünde, yerine koyma veya yok etme yöntemleri kullanılabilir veya doğruların grafiklerinden de faydalanılabilir.
İKİ BİLİNMEYENLİ DOĞRUSAL DENKLEM SİSTEMLERİ
Bir pastanede pazar günü meyveli ve çikolatalı olmak üzere toplam 13 tane pasta satılmıştır. Meyveli pastanın tanesi 25 TL, çikolatalı pastanın tanesi 40 TL’dir. Pastane bu iki pasta satışından 460 TL kazandığına göre, kaçar tane meyveli ve çikolatalı pasta satıldığını bulalım.
Problemde verilenlere uygun denklemleri yazalım.
Satılan meyveli pasta sayısı x, satılan çikolatalı pasta sayısı y olsun. Bu durumda aşağıdaki denklemler yazılır.
x + y = 13
25x + 40y = 460
Yazdığımız iki denklem doğrusal denklem sistemi oluşturur. Doğrusal denklem sistemlerinin çözümünde yerine koyma veya yok etme yöntemi kullanılır.
Doğrusal denklem sisteminin çözümü olan (x, y) sıralı ikilisi her iki denklemi de sağlamalıdır. Oluşturduğumuz doğrusal denklem sistemini iki yöntemle de çözelim.
Yerine koyma yönteminde; doğrusal denklemlerden herhangi biri kullanılarak bilinmeyenlerden biri diğeri cinsinden yazılır, Diğeri cinsinden elde edilen cebirsel ifade, kullanılmayan diğer doğrusal denklemde yerine yazılarak bir bilinmeyenli denklem elde edilir. Elde edilen bir bilinmeyenli denklem çözülerek bilinmeyenlerden birinin değeri bulunur. Bulunan bilinmeyenin değeri doğrusal denklemlerden herhangi birinde yerine yazılarak diğer bilinmeyenin değeri bulunur.
Yok etme yönteminde; doğrusal denklem sisteminde bilinmeyenlerden en az birinin kat sayılarının toplama işlemine göre birbirinin tersi olup olmadığına bakılır. İki bilinmeyenin de kat sayıları farklı ise bilinmeyenlerden biri seçilerek kat sayıları, eşitliğin her iki tarafı aynı sayı ile çarpılarak veya bölünerek toplama işlemine göre birbirinin tersi olması sağlanır. Kat sayıları düzenlenen doğrusal denklemler taraf tarafa toplanarak bilinmeyenlerden biri yok edilip bir bilinmeyenli denklem elde edilir. Elde edilen bir bilinmeyenli denklem çözülür. Bulunan bilinmeyenin değeri denklemlerden herhangi birinde yerine yazılarak diğer bilinmeyenin değeri bulunur
DOĞRUSAL DENKLEM SİSTEMLERİNİN GRAFİKLERİ
Ayşe ve Berna performans ödevlerini yapmak için kütüphanede buluşacaklardır. İkisi de kütüphaneye bisikletleriyle gitmişlerdir. İkisi bisikletleriyle toplam 5 km yol almışlardır. Berna, Ayşe’den 3 km daha fazla yol aldığına göre, ikisinin aldıkları yolları bulalım.
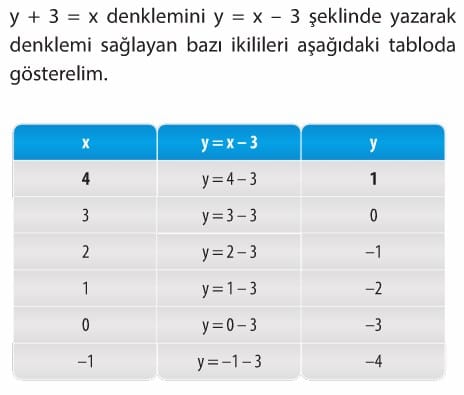
Bunun için problemde verilen durumlara uygun denklemleri yazalım. Berna’nın aldığı yol x km, Ayşe’nin aldığı yol y km o|sun.Toplam alınan yol 5 km olduğundan, x + y = 5 yazılır. Berna, Ayşe’den 3 km daha fazla yol aldığından, y + 3 = x yazılır. y + x = 5 denklemi ile y + 3 = x denklemi iki değişkenden oluşan doğrusal denklemlerdir. Her iki denklemin de çözümü sınırsız (x, y) ikililerinden oluşur.
Denklem Sistemleri konu anlatımı 8.sınıf matematik
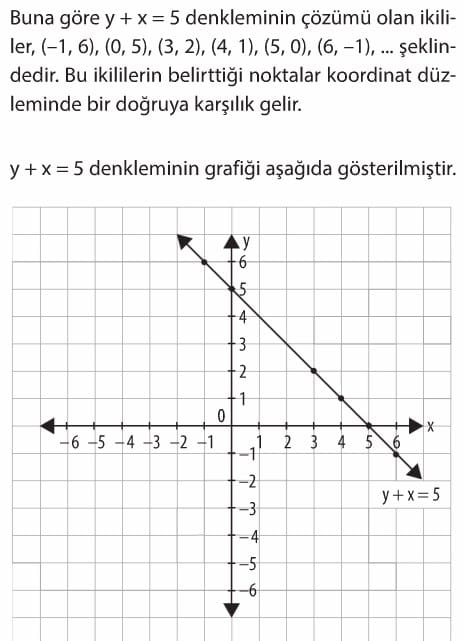
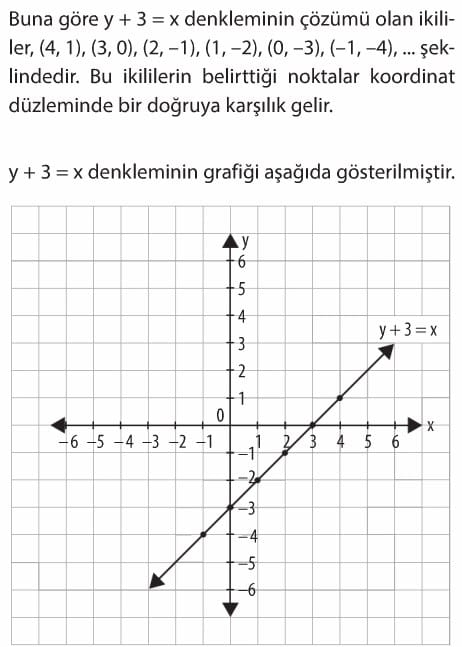
Buna göre y + x = 5 denkleminin çözümü olan ikililer, (-1, 6), (0, 5), (3, 2), (4, 1), (5, 0), (6, -1), şeklindedir. Bu ikililerin belirttiği noktalar koordinat düzleminde bir doğruya karşılık gelir.
y + x = 5 denkleminin grafiği aşağıda gösterilmiştir.
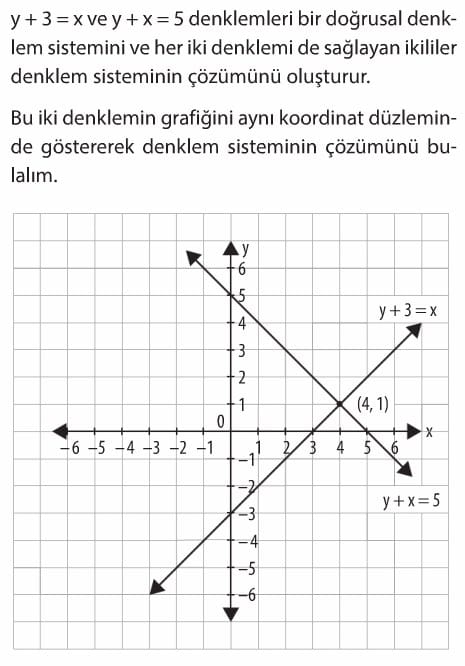
y + 3 = x ve y + x = 5 denklemleri bir doğrusal denklem sistemini ve her iki denklemi de sağlayan ikililer denklem sisteminin çözümünü oluşturur.
Bu iki denklemin grafiğini aynı koordinat düzleminde göstererek denklem sisteminin çözümünü bulalım.
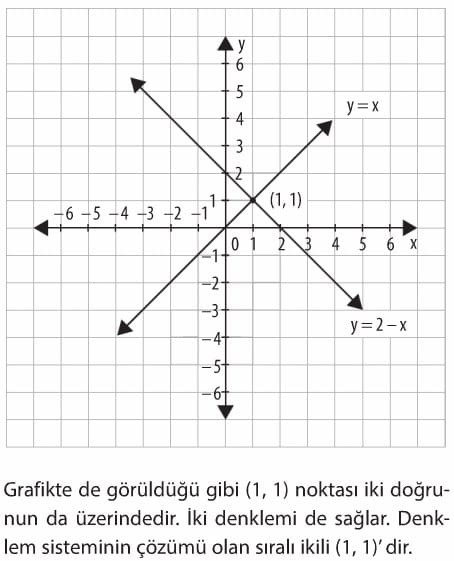
y=2-x
y = x
doğrusal denklem sisteminin çözümü olan sıralı ikiliyi denklemlerin grafiklerinden faydalanarak bulalım. Denklemlerin grafiklerinden faydalanarak çözümü bulmak için her bir denklemin grafiğini çizelim.
y = 2 - x denkleminin grafiğini çizelim.
x=0 içiny=2-x
y=2-0
y = 2'dir.
y = 2 - x denkleminin grafiği y eksenini (0, 2) noktasında keser.
y=0 için y=2-x
0=2-x
x=2'dir.
y = 2 - x denkleminin grafiği x eksenini (2, 0) noktasında keser.
y = x denkleminin grafiğini çizelim.
x = 0 için y = 0'dır.
y = x denkleminin grafiği orijinden geçer.
x =1 için y = 1'dir.
y = x denkleminin grafiği (1, 1) noktasından geçer. Denklemlerin grafiklerini aynı kartezyen koordinat sisteminde gösterelim. Grafikte de görüldüğü gibi (1, 1) noktası iki doğrunun da üzerindedir. İki denklemi de sağlar. Denklem sisteminin çözümü olan sıralı ikili (i, 1)'dir.