Çarpanlara Ayırma (8.sınıf)
Tanım: Bir cebirsel ifadeyi çarpanlarının çarpımı şeklinde yazmaya 0 cebirsel ifadeyi çarpanlarına ayırma denir.
Buna göre, bir ifadeyi çarpanlarına ayırmak demek; ifadeyi iki terimli veya daha çok terimli ifadelerin çarpımı şeklinde yazmak demektir.
Ortak çarpan Parantezine Alma
Bir cebirsel ifadenin her bir terimindeki ortak çarpanların, parantez dışına alınıp terimlerin çarpımı biçiminde yazılmasına bu cebirsel ifadeyi ortak çarpan parantezine almak denir.
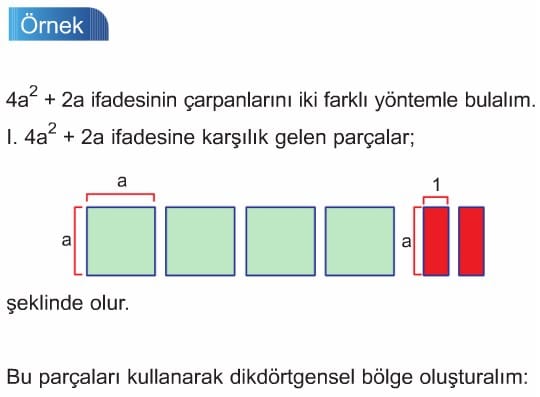
Örnek: 2x + 4 ifadesinin çarpanlarını iki farklı yöntemle bulalım.
I. 2x + 4 ifadesine karşılık gelen parçalar;
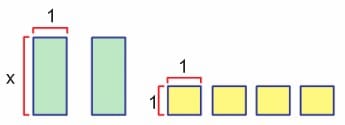
şeklinde olur. Bu parçaları kullanarak dikdörtgensel bölge oluşturalım.
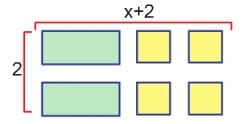
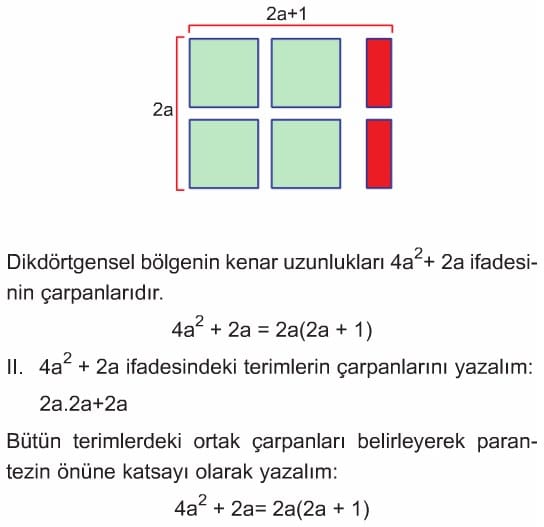
Dikdörtgensel bölgenin kenar uzunlukları 2x + 4 ifadesinin çarpanlarıdır.
II. 2x + 4 ifadesindeki terimlerin çarpanlarını yazalım.
2x + 2.2
Bütün terimlerdeki ortak çarpanları belirleyerek parantezin önüne katsayı olarak yazalım.
2x + 4 = 2(x + 2)
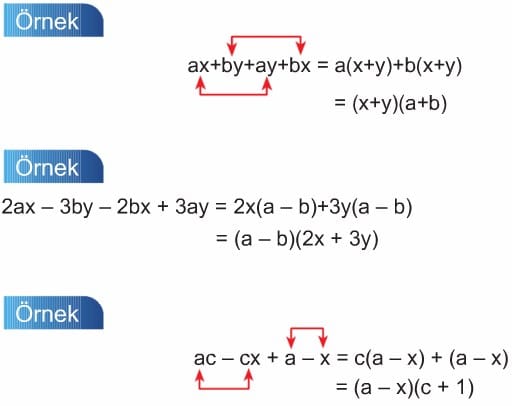
Gruplandırarak Çarpanlara Ayırma
Verilen ifadenin terimleri uygun şekillerde gruplara ayrılır. Ayrılan gruplarda ortak bir çarpan bulunur ve ortak çarpan parantezine alınır.
İki Kare Farkı şeklindeki İfadeleri Çarpanlarına Ayırma
a2 – b2 biçimindeki ifadeleri çarpanlarına ayırmak için birinci ve ikinci terimin karekökü alınır. Bulunan terimler, toplamları ile farklarının çarpımı biçiminde yazılır.
a2 – b2 = (a + b).(a – b)