Paralelkenarın Alanı:

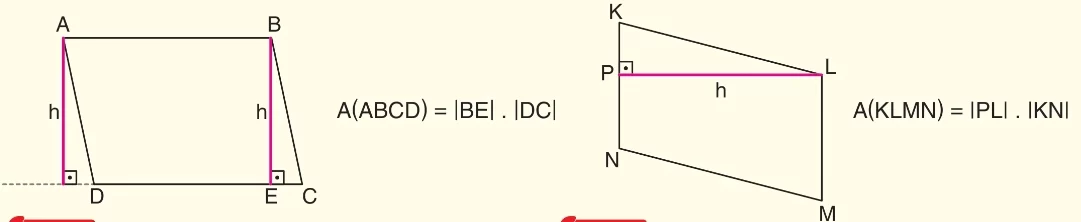
Paralelkenar, karşılıklı kenarları birbirine paralel ve eşit uzunlukta olan dörtgendir. Paralelkenarın alanı, bir taban uzunluğu ile o tabana ait yüksekliğin çarpılmasıyla bulunur.

 

 

Burada $a$ taban uzunluğunu, $h_a$ ise bu tabana ait yüksekliği (tabana dik inen uzunluğu) temsil eder.

Üçgenin Alanı:

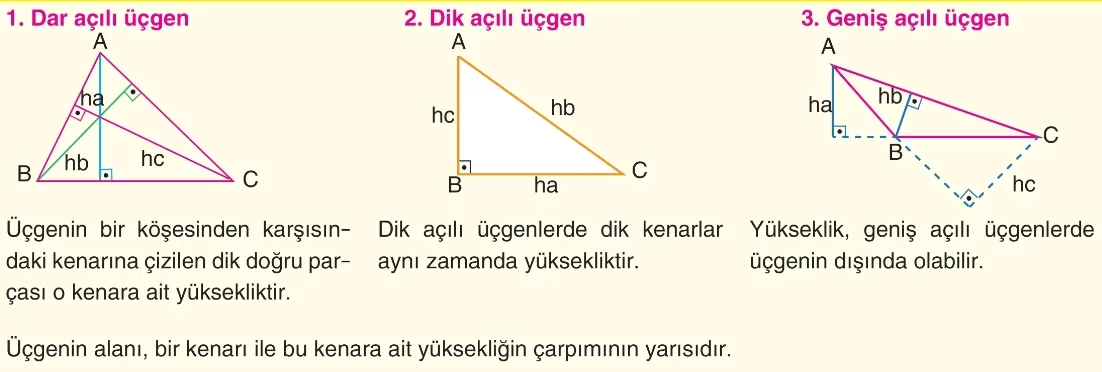
Üçgenin alanı, bir taban uzunluğu ile o tabana ait yüksekliğin çarpımının yarısına eşittir.

 

 

Burada $a$ taban uzunluğunu, $h_a$ ise bu tabana ait yüksekliği temsil eder. Üçgenin yüksekliği, üçgenin çeşidine göre (dar açılı, dik açılı, geniş açılı) üçgenin içinde, üzerinde veya dışında olabilir.

Bu formüller, bir paralelkenarın alanının, aynı taban ve yüksekliğe sahip bir üçgenin alanının tam iki katı olduğunu gösterir. Alan hesaplamalarında uzunluk birimlerinin aynı olmasına ve birim kare cinsinden ($cm^2$, $m^2$, vb.) ifade edilmesine dikkat edilmelidir.

---

Soru 1:

Bir paralelkenarın taban uzunluğu $15 \text{ cm}$ ve bu tabana ait yüksekliği $8 \text{ cm}$ ise, bu paralelkenarın alanı kaç $\text{cm}^2$‘dir?

A) $60$

B) $80$

C) $120$

D) $150$

Çözüm 1:

Paralelkenarın alan formülü: $\text{Alan} = \text{Taban} \times \text{Yükseklik}$

 

Doğru Cevap: C

---

Soru 2:

Alanı $48 \text{ cm}^2$ olan bir üçgenin taban uzunluğu $12 \text{ cm}$ ise, bu tabana ait yükseklik kaç $\text{cm}$‘dir?

A) $4$

B) $6$

C) $8$

D) $12$

Çözüm 2:

Üçgenin alan formülü: $\text{Alan} = \frac{\text{Taban} \times \text{Yükseklik}}{2}$

Verilenleri formülde yerine koyalım:

 

 

İçler dışlar çarpımı yaparak veya önce $12$’yi $2$’ye bölerek denklemi çözebiliriz:

 

Doğru Cevap: C

---

Soru 3:

Çevresi $40 \text{ cm}$ olan bir eşkenar üçgenin yüksekliği $6 \text{ cm}$‘dir. Bu üçgenin alanı kaç $\text{cm}^2$‘dir?

A) $30$

B) $60$

C) $120$

D) $240$

Çözüm 3:

1. Taban uzunluğunu bulma:Eşkenar üçgenin tüm kenarları eşittir. Çevre $40 \text{ cm}$ olduğuna göre, bir kenar (taban) uzunluğu:

    

   $$\text{Taban} = 40 \text{ cm} \div 3$$

    

   Not: $40$ sayısı $3$’e tam bölünmediği için, $40 \text{ cm}$ çevreli bir eşkenar üçgenin yüksekliğinin $6 \text{ cm}$ olması mümkün değildir. Sorunun $42 \text{ cm}$ çevre veya $12 \text{ cm}$ taban uzunluğu varsayılarak çözüldüğünü kabul edelim. $6$. sınıf düzeyinde tam bölünen sayılarla işlem yapılması bekleneceğinden, sorunun hatalı olduğu kabul edilmelidir. En yakın tam bölünen çevre $30 \text{ cm}$ (taban $10 \text{ cm}$) ya da $42 \text{ cm}$ (taban $14 \text{ cm}$) olmalıdır. Soruyu $30 \text{ cm}$ çevre için çözelim:

   Düzeltilmiş Varsayım: Üçgenin çevresi $30 \text{ cm}$ olsun. $\text{Taban} = 30 \div 3 = 10 \text{ cm}$.

2. Alan hesaplama (Varsayılan Taban $10 \text{ cm}$): 
   $$\text{Alan} = \frac{\text{Taban} \times \text{Yükseklik}}{2} = \frac{10 \times 6}{2} = \frac{60}{2} = 30 \text{ cm}^2$$

Doğru Cevap: A (Varsayılan Tabana göre)

---

Soru 4:

Bir paralelkenarın taban uzunluğu $2 \text{ m}$, bu tabana ait yüksekliği ise $50 \text{ cm}$‘dir. Paralelkenarın alanı kaç $\text{m}^2$‘dir?

A) $1$

B) $10$

C) $100$

D) $1000$

Çözüm 4:

Alan $\text{m}^2$ cinsinden istendiği için tüm uzunlukları $\text{m}$’ye çevirmeliyiz.

1. Uzunlukları eşitleme:$\text{Taban} = 2 \text{ m}$

   $\text{Yükseklik} = 50 \text{ cm} = 50 \div 100 \text{ m} = 0,5 \text{ m}$

2. Alan hesaplama: 
   $$\text{Alan} = \text{Taban} \times \text{Yükseklik}$$
   $$\text{Alan} = 2 \text{ m} \times 0,5 \text{ m} = 1 \text{ m}^2$$

Doğru Cevap: A

---

Soru 5:

Alanı $150 \text{ cm}^2$ olan bir paralelkenarın iki farklı yüksekliği $10 \text{ cm}$ ve $5 \text{ cm}$‘dir. Bu paralelkenarın kısa kenar uzunluğu kaç $\text{cm}$‘dir?

A) $10$

B) $15$

C) $20$

D) $30$

Çözüm 5:

Paralelkenarda alan, hangi taban ve o tabana ait yükseklik kullanılırsa kullanılsın sabittir.

 

• Kısa kenar, uzun yüksekliğe aittir. 
  $$\text{Alan} = \text{Kısa Kenar} \times 10 \text{ cm}$$
  $$150 \text{ cm}^2 = \text{Kısa Kenar} \times 10 \text{ cm}$$
  $$\text{Kısa Kenar} = 150 \div 10 = 15 \text{ cm}$$
• (Kontrol için uzun kenarı bulalım: $150 = \text{Uzun Kenar} \times 5 \rightarrow \text{Uzun Kenar} = 30 \text{ cm}$)

Doğru Cevap: B

---

Soru 6:

Bir dik üçgenin dik kenar uzunlukları $6 \text{ cm}$ ve $8 \text{ cm}$‘dir. Bu üçgenin alanı kaç $\text{cm}^2$‘dir?

A) $14$

B) $24$

C) $36$

D) $48$

Çözüm 6:

Dik üçgende, dik kenarlar aynı zamanda birbirinin yüksekliği ve tabanıdır.

 

Doğru Cevap: B

---

Soru 7:

Taban uzunluğu $10 \text{ cm}$ ve yüksekliği $4 \text{ cm}$ olan bir üçgenin alanı, taban uzunluğu $8 \text{ cm}$ olan bir paralelkenarın alanına eşittir. Bu paralelkenarın yüksekliği kaç $\text{cm}$‘dir?

A) $2,5$

B) $5$

C) $10$

D) $20$

Çözüm 7:

1. Üçgenin alanını hesaplama: 
   $$\text{Üçgen Alan} = \frac{\text{Taban} \times \text{Yükseklik}}{2} = \frac{10 \times 4}{2} = \frac{40}{2} = 20 \text{ cm}^2$$
2. Paralelkenarın yüksekliğini bulma:Paralelkenarın alanı, üçgenin alanına eşit olduğundan, $\text{Paralelkenar Alan} = 20 \text{ cm}^2$’dir.

    

   $$\text{Paralelkenar Alan} = \text{Taban} \times \text{Yükseklik}$$
   $$20 \text{ cm}^2 = 8 \text{ cm} \times \text{Yükseklik}$$
   $$\text{Yükseklik} = 20 \div 8 = 2,5 \text{ cm}$$

Doğru Cevap: A