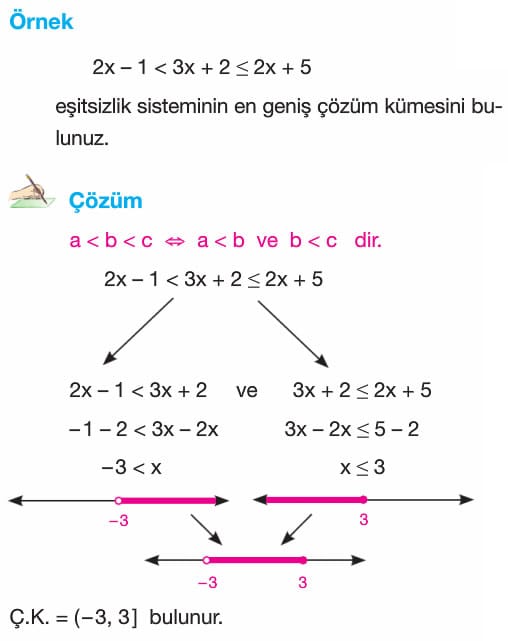
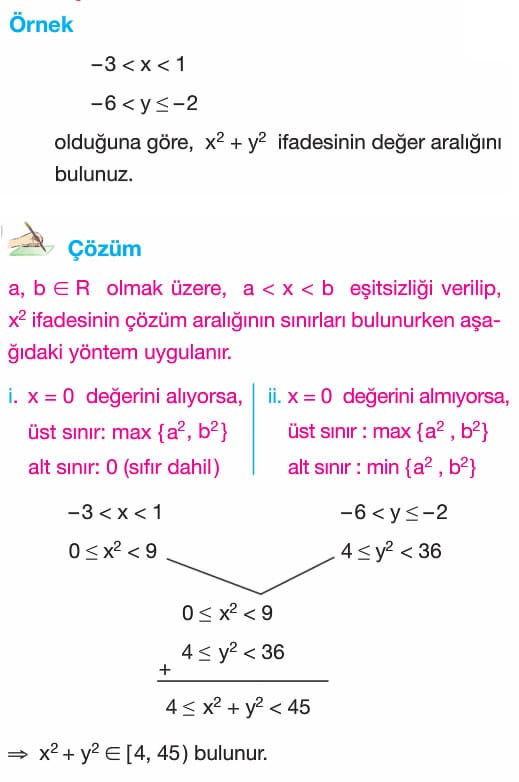
Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler Çözümlü Sorular ve Testler 9. Sınıf
Konu hakkında eksikleriniz varsa Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler Konu Anlatımı yazımıza bakmanızı tavsiye ederiz.
Sonraki Konu: Mutlak Değer İçeren Denklem ve Eşitsizlikler
Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler Online Testler
Birinci Dereceden Basit Eşitsizlikler Test 1 Çöz
Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler Çözümlü Sorular
Soru 1 (Yeni Nesil Soru):
Bir çiftlikte 3 çeşit hayvan bulunmaktadır: tavuk, koyun ve inek. Tavuklar günde 2 kilogram, koyunlar 4 kilogram, inekler ise 8 kilogram yem tüketmektedir. Çiftlik sahibi, günlük toplam yem tüketiminin 150 kilogramı geçmemesi gerektiğini belirtiyor. Eğer çiftlikte toplam 10 tavuk ve 5 koyun varsa, en fazla kaç inek çiftlikte bulundurulabilir?
A) 5
B) 8
C) 10
D) 12
E) 15
Çözüm:
Tavukların günlük yem tüketimi 10 . 2 = 20 kilogramdır.
Koyunların günlük yem tüketimi 5 . 4 = 20 kilogramdır.
Bu durumda toplam 40 kilogramlık bir tüketim vardır. Geriye 150 – 40 = 110 kilogram kalıyor.
İneklerin yem tüketimi 8 kilogram olduğuna göre, en fazla kaç inek olabilir bulalım:
110 / 8 = 13.75, yani en fazla 13 inek olabilir. Ancak seçeneklerde en yakın değer 12 olduğundan, cevap 12’dir.
Cevap: D
Soru 2 (Yeni Nesil Soru):
Bir marketin indirim kampanyasında her alınan çikolata için 3 lira, her alınan içecek için 5 lira ödeme yapılmaktadır. Bir müşteri en fazla 50 lira harcamayı planlıyor ve 4 çikolata aldı. Buna göre, müşteri en fazla kaç içecek alabilir?
A) 6
B) 7
C) 8
D) 9
E) 10
Çözüm:
Müşteri 4 çikolata aldığına göre, 4 . 3 = 12 lira öder. Geriye kalan para 50 – 12 = 38 liradır.
Her içecek 5 lira olduğuna göre, en fazla kaç içecek alınabilir:
38 / 5 = 7.6, yani en fazla 7 içecek alınabilir.
Cevap: B
Soru 3 (Yeni Nesil Soru):
Bir spor salonu, aylık üyelik bedeli olarak başlangıçta 50 lira alıp, her antrenman için 10 lira ek ücret almaktadır. Ahmet en fazla 200 lira harcayabileceğini belirtmiştir. Bu durumda Ahmet, en fazla kaç antrenman yapabilir?
A) 15
B) 14
C) 13
D) 12
E) 10
Çözüm:
Ahmet’in başlangıçta ödediği ücret 50 liradır. Geriye 200 – 50 = 150 lira kalır.
Her antrenman 10 lira olduğuna göre, en fazla kaç antrenman yapılabilir:
150 / 10 = 15 antrenman yapılabilir.
Cevap: A
Soru 4 (Yeni Nesil Soru):
Bir araba kiralama firması, kiralanan her gün için sabit 100 lira ücret alırken, toplam kilometre başına 2 lira ek ücret almaktadır. Müşteri en fazla 500 lira ödemek istiyorsa, 3 gün boyunca arabayı kiralayarak en fazla kaç kilometre yol yapabilir?
A) 50
B) 100
C) 150
D) 200
E) 250
Çözüm:
3 gün için sabit ücret 3 . 100 = 300 liradır.
Geriye kalan para 500 – 300 = 200 liradır.
Her kilometre başına 2 lira ödendiğine göre, en fazla kaç kilometre yol yapılabilir:
200 / 2 = 100 kilometre.
Cevap: B
Soru 5 (Yeni Nesil Soru):
Bir restoranda menüdeki yemekler ortalama 15 lira, tatlılar ise ortalama 7 liradır. Bir grup arkadaş en fazla 150 lira harcamayı planlamaktadır. Eğer 6 yemek sipariş etmişlerse, en fazla kaç tatlı alabilirler?
A) 6
B) 7
C) 8
D) 9
E) 10
Çözüm:
6 yemeğin toplam ücreti 6 . 15 = 90 liradır.
Geriye kalan para 150 – 90 = 60 liradır.
Her tatlı 7 lira olduğuna göre, en fazla kaç tatlı alınabilir:
60 / 7 = 8.57, yani en fazla 8 tatlı alınabilir.
Cevap: C